
- •1.Абсолютная и относительная погрешности измерения
- •2. Систематические и случайные погрешности
- •3. Сведения из теории вероятностей
- •1. Порядок аналитической обработки результатов прямых измерений 6
- •6. Оценка доверительной границы погрешности косвенных измерений 6
- •4. Оценка случайных погрешностей прямых измерений
- •Порядок аналитической обработки результатов прямых измерений
- •6. Оценка доверительной границы погрешности косвенных измерений
- •1. Расчет абсолютной погрешности измерения по классу точности прибора
- •Пример расчета погрешности косвенных измерений
- •1. Пример расчета погрешности косвенного измерения частоты f по формуле 13. Для периода
- •2. Пример расчета погрешности косвенного измерения индуктивности l по формуле (13)
- •3 Лист 8, 5 1-я сторона
Ульяновский государственный университет
Кафедра ФМПИ
Дисциплина физика
Гурина Р.В.
-
Погрешности измерений
Методическая разработка
практического занятия
2011
Погрешности результатов измерений физических величин
Прямые измерения
Прямыми измерениями называют такие измерения, при которых с помощью эталонного прибора измеряют непосредственно исследуемую величину X. Например, прямым измерением является измерение длины при помощи линейки.
Косвенные измерения
Косвенными измерениями называют такие измерения, при которых искомое значение величины находится на основании известной зависимости между этой величиной и величинами, определяемыми прямыми измерениями. Примером косвенных измерений является измерение плотности тела по результатам прямых измерений его массы и объема.
1.Абсолютная и относительная погрешности измерения
Абсолютная
погрешность
и![]() змерения
- это разность между измеренным
змерения
- это разность между измеренным
![]() и истинным значением
измеряемой
величины:
и истинным значением
измеряемой
величины:![]() (1)
(1)
Относительная погрешность измерении 6 равна отношению абсолютной погрешности измерении к истинному значении) измеряемой величины:
 (2)
(2)
Истинное значение измеряемой величины А'<> экспериментатору не известно. Наиболее близко к истинному значению лежит среднее значение измеряемой величины, определяемое по формуле
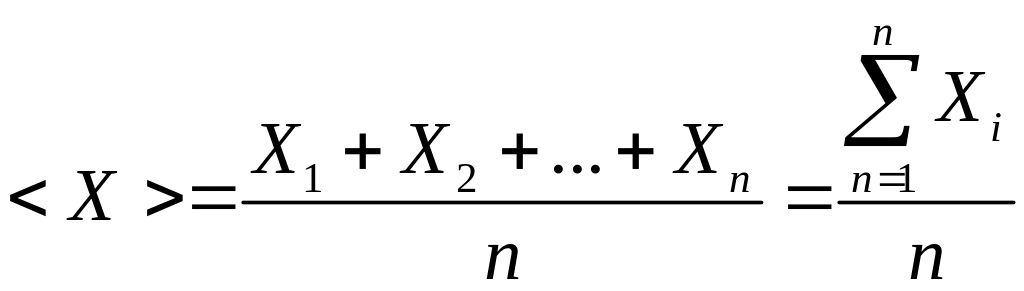
4
1. Порядок аналитической обработки результатов прямых измерений 6
6. Оценка доверительной границы погрешности косвенных измерений 6
7. Порядок аналитической обработки ре<ультатов косвенных измерений 7
![]() (3)
(3)
Среднее значение абсолютной погрешности
 (4)
(4)
2. Систематические и случайные погрешности
Систематическая погрешность измерения — это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющейся при измерениях. Она может быть вызвана неточностью метода измерения, погрешностями приборов и другими причинами.
Случайная погрешность измерения — это составляющая погрешности измерения, изменяющаяся случайным образом.
3. Сведения из теории вероятностей
При
многократных измерениях одной и той же
величины получается набор значений
![]() которые представляют собой набор
случайных величин. Соответственно
случайными величинами являются и
абсолютные погрешности
которые представляют собой набор
случайных величин. Соответственно
случайными величинами являются и
абсолютные погрешности![]() ,.
Распределение таких величин, согласно
теории вероятностей, подчиняется
нормальному
закону распределения Гаусса
и описывается формулой
,.
Распределение таких величин, согласно
теории вероятностей, подчиняется
нормальному
закону распределения Гаусса
и описывается формулой
 (5)
(5)
где
![]() функция,
характеризующая вероятность погрешности
при измерении
х,
функция,
характеризующая вероятность погрешности
при измерении
х,![]() среднее квадратичное отклонение
случайной величины от среднего
значения.
среднее квадратичное отклонение
случайной величины от среднего
значения.
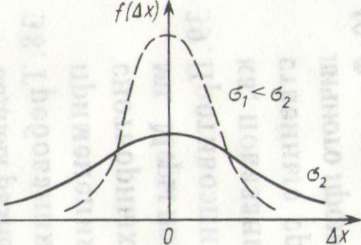
Рис. 1
Поскольку
с
раиной вероятностью может быть как
больше, так и меньше нуля, то среднее
значение
![]() стремится
к 0 с
ростом числа измерений. График зависимости
дан на рис. 1.
С ростом о максимум кривой Гаусса
убывает,
стремится
к 0 с
ростом числа измерений. График зависимости
дан на рис. 1.
С ростом о максимум кривой Гаусса
убывает,
но площадь под кривой остается постоянной, что связано с условием нормировки
 (6)
(6)
которое
означает, что вероятность попадания
случайной величины
в
интервал
![]() равна
1. Соответственно величина
равна
1. Соответственно величина
![]() (7)
(7)
4
1. Порядок аналитической обработки результатов прямых измерений 6
6. Оценка доверительной границы погрешности косвенных измерений 6
7. Порядок аналитической обработки ре<ультатов косвенных измерений 7
Значение
стремится к своему точному значению с
ростом n.
Назовем доверительной границей
погрешности
![]() величину
величину
![]() ,
если
попадает в интервал
,
если
попадает в интервал
![]() |
с заданной вероятностью р. Очевидно,
что с ростом
|
с заданной вероятностью р. Очевидно,
что с ростом
![]() должно
расти и
.
При проведении лабораторных работ
рекомендуется выбирать р = 0,9.
должно
расти и
.
При проведении лабораторных работ
рекомендуется выбирать р = 0,9.
Теория
вероятности позволяет связать
с
![]() :
:
![]() (10)
(10)
Где t - коэффициент Стьюдента, зависящий от числа измерений n и доверительной вероятности р (см. табл.).
4. Оценка случайных погрешностей прямых измерений
Оценить доверительную границу случаи погрешности можно по формуле (10).
Таблица
Для p=0.9
Число измерений n |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
30 |
∞ |
Коэффициент Стьюдента |
2,9 |
2,4 |
2,1 |
2,0 |
1,9 |
1,9 |
1,9 |
1,9 |
1,7 |
1,645 |
При
прямых измерениях, когда результаты
отдельных измерений одинаковы
![]() ,
доверительная граница погрешности
оценивается по приборной погрешности
согласно выражению
,
доверительная граница погрешности
оценивается по приборной погрешности
согласно выражению
 (11)
(11)
где
для
р =
0,9
![]() =
1,045 (см. табл.),
=
1,045 (см. табл.),
![]() -
либо абсолютная максимальная погрешность
прибора, либо половина цены его наименьшего
деления.
-
либо абсолютная максимальная погрешность
прибора, либо половина цены его наименьшего
деления.
Если значение доверительной границы, рассчитанное по формуле (10), сравнимо со значением приборной погрешности, рассчитанной по формуле (11), то результирующая погрешность измерения находится следующим образом:
 (12)
(12)
