
- •Исследование характеристик Интегрирующей и дифференцирующей rc-цепей
- •P X Expression y Expression
- •P X Expression y Expression
- •Исследование схемы усилителя с общим эмиттером
- •Component Analog Primitives Waveform Sources Sine source 60Hz
- •P X Expression y Expression
- •P X Expression y Expression
- •P X Expression y Expression
- •Исследование схем инвертирующего и неинвертирующего усилителей на оу
- •Component Analog Primitives Waveform Sources Sine source 60Hz
- •P X Expression y Expression
- •P X Expression y Expression
- •Библиографический список
- •Исследование схемы генератора синусоидальных колебаний на оу
- •Component Analog Library Opamp lf0000- lm741- lm741
- •Component Analog Primitives Waveform Sources Sine source General
- •P X Expression y Expression
- •Библиографический список
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Омский государственный технический университет»
А Н А Л О Г О В Ы Е Э Л Е К Т Р О Н Н Ы Е Ц Е П И
Методические указания к лабораторным работам
по дисциплине «Электронные цепи и микросхемотехника»
Омск 2007
Составитель Д.Г. Лобов, канд. техн. наук
Печатается по решению редакционно-издательского совета Омского государственного технического университета
ЛАБОРАТОРНАЯ РАБОТА № 1
Исследование характеристик Интегрирующей и дифференцирующей rc-цепей
Цель работы
Исследование амплитудно-частотных, фазочастотных и переходных характеристик интегрирующей и дифференцирующей RC-цепей.
Пояснения к работе
Схемы интегрирующей и дифференцирующей RC-цепей изображены на рис. 1.
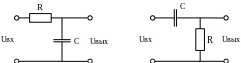
а) б)
Рис. 1. Схемы: а) интегрирующей и б) дифференцирующей RC-цепей
Для нахождения комплексного коэффициента передачи каждой из представленных цепей можно воспользоваться формулой делителя напряжения:
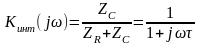 , (1)
, (1)
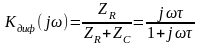 , (2)
, (2)
где ZC = 1/jωC – комплексное сопротивление конденсатора, ZR = R-комплексное сопротивление резистора, τ – постоянная времени RC-цепи:
τ = RC. (3)
АЧХ (в децибелах) и ФЧХ RC-цепей находятся из формул (1) и (2), соответственно для интегрирующей цепи:
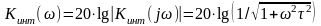 , (4)
, (4)
 ,
(5)
,
(5)
а для дифференцирующей цепи:
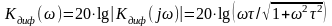 ,
(6)
,
(6)
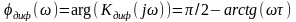 .
(7)
.
(7)
При построении графиков АЧХ и ФЧХ (4)…(7) удобно ввести понятие частоты среза RC-цепей
ωср = 1/τ (8)
и изображать данные графики в относительном логарифмическом масштабе по оси частот, как представлено на рис. 2.
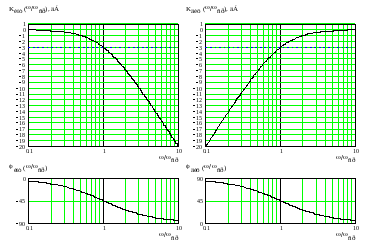
Рис. 2. Графики АЧХ и ФЧХ интегрирующей и дифференцирующей RC-цепей
Как следует из рис. 2, на частоте ω = 0,1ωср коэффициент передачи интегрирующей RC-цепи практически равен 0 дБ (т.е. ослабление сигнала отсутствует), на частоте ω = 10ωср коэффициент передачи уменьшается до значения -20 дБ (что соответствует 10-кратному ослаблению сигнала), а на частоте
ω = ωср ослабление составляет -3 дБ (пунктирная линия на графиках АЧХ). Таким образом, интегрирующая RC-цепь хорошо пропускает сигналы с частотами, лежащими ниже ωср, и ослабляет сигналы с частотами, большими, чем ωср. Следовательно, интегрирующая RC-цепь представляет собой простейший фильтр нижних частот. Такой фильтр является фильтром I порядка, т.к. содержит один реактивный элемент (конденсатор). Наклон АЧХ в области высоких частот составляет -20 дБ/дек.
Дифференцирующая RC-цепь, наоборот, хорошо пропускает сигналы с частотами выше ωср и ослабляет сигналы на частотах, меньших ωср, поэтому данная цепь является фильтром верхних частот I порядка. Наклон АЧХ в области низких частот составляет -20дБ/дек.
Переходная характеристика представляет собой переходной процесс, происходящий в электрической цепи при подаче на её вход прямоугольного сигнала. Для выходного напряжения интегрирующей цепи он определяется выражением
Uинт(t) = U0∙(1 – exp(-t/τ)),
где U0 – амплитуда входного прямоугольного сигнала.
Для дифференцирующей цепи соответственно
Uдиф(t) = U0∙exp(-t/τ).
Графики, иллюстрирующие переходные характеристики цепей, представлены на рис. 3. Амплитуда входного прямоугольного сигнала U0 принята равной 1В, а масштаб по оси абсцисс задан в относительных единицах, кратных постоянной времени цепи τ.

Рис. 3. Переходные характеристики интегрирующей
и дифференцирующей RC-цепей
Из графиков рис. 3 видно, что у интегрирующей RC-цепи в процессе заряда конденсатора выходное напряжение постепенно возрастает, со временем достигая установившегося значения, равного амплитуде входного сигнала. У дифференцирующей RC-цепи в первый момент времени выходное напряжение скачком изменяется до максимального значения (оно также равно амплитуде входного сигнала), а затем, в процессе заряда конденсатора, постепенно убывает до нуля.
Для оценки переходного процесса вводится параметр, называемый временем установления tуст. Он определяет интервал времени с момента подачи входного напряжения до момента, когда можно считать, что процесс установления выходного сигнала завершился. Для интегрирующей и дифференцирующей RC-цепей tуст выбирают в пределах (3…5)τ.
При t = 3τ выходное напряжение интегрирующей RC-цепи достигает 95 % от установившегося, при t = 5τ – соответственно 99,3 % от установившегося. Через время t = τ выходное напряжение достигает 63 % от установившегося значения (пунктирная линия на графиках переходных характеристик).
У дифференцирующей цепи при t = 3τ выходное напряжение уменьшается до значения 5 % от максимального, а при t = 5τ – до 0,7 % от максимального значения. Через время t = τ выходное напряжение уменьшается до 37 % от максимального значения.
Порядок проведения лабораторной работы
По заданной преподавателем частоте среза fср рассчитать циклическую частоту среза ωср = 2πfср, затем из формулы (8) определить постоянную времени .
Задать номинал емкости С, произвольно выбрав его из ряда Е12 (рекомендуется выбирать емкость в переделах 1…10 нФ), после чего по известной постоянной времени из формулы (3) рассчитать величину сопротивления и выбрать ближайший к расчётному номинал R из ряда Е24.
Нарисовать схему интегрирующей RC-цепи в Microcap.
Установить на вход схемы модель источника ЭДС, выбрав его тип из меню: Component Analog Primitives Waveform Sources Pulse Sourse SQUARE
Произвести расчет АЧХ и ФЧХ схемы (в логарифмическом масштабе), воспользовавшись меню: Analysis AC Analysis, при этом необходимо указать следующие параметры:
Frequency Range 10fср,0.1fср (указать численные значения!) Run Options Normal
Number of Points 100 State Variables Zero
Temperature 27 Frequency Step Auto
Max. Change % 5
Noise Input None Auto Scale Ranges
Noise Output None
