
- •Актуарная математика. Глава №2. Теория процентных ставок.
- •§2.1 Ставка процента.
- •§2.2 Номинальная процентная ставка.
- •§2.3 Факторы накопления.
- •§2.4 Интенсивность процента.
- •§2.5 Текущая стоимость (настоящая стоимость).
- •Решение: Для величину можно определить как , а для . Это даёт
- •§2.6 Формула Студли для интенсивности процента.
- •§2.7 Текущие стоимости потоков наличности.
- •Дискретные потоки наличности.
- •Непрерывно выплачиваемые потоки наличности.
- •Пример 2.7.1: Пусть время измеряется в годах и
- •§2.8 Оцениваемые(valuing) потоки наличности.
- •§2.9 Процентный доход.
- •§2.10 Капитальные прибыли и убытки, налоги.
- •Глава №3.
- •§3.1 Основные функции сложных процентов.
- •§3.2 Уравнение стоимости и доход от сделки.
- •§3.3 Ренты: текущие стоимости и накопления.
- •§3.4 Отсроченные ренты.
- •§3.5 Непрерывно выплачиваемые ренты.
- •§3.6 Изменяющиеся ренты.
- •§3.7 Общая схема заёма.
- •§3.8 Схема заёма для level ренты.
- •Глава №4. Номинальные ставки процента. Ренты, выплачиваемые p раз.
- •§4.1 Процент, выплачиваемый p раз.
- •Решение:
- •Пример 4.1.3: Пусть и - положительные целые. Выразить в терминах . Найти когда . Решение: .
- •§4.2 Ренты, выплачиваемые p раз: текущие стоимости и накопления.
- •Глава №5. Дисконтированный поток наличности.
- •§5.1 Чистые потоки наличности.
- •§5.2 Чистые текущие стоимости и доходы.
- •§5.3 Сравнение двух инвестиционных проектов.
- •§5.4 Различные процентные ставки для заёмщиков и аккредиторов.
- •§5.5 Потоки инфляции.
- •§5.6 Доход фонда.
- •§5.7 Измерение инвестиционного performance.
§3.8 Схема заёма для level ренты.
Рассмотрим особый случай, когда на базе процентной ставки сумма займа делается в момент 0 при условии возвращения в выплатах, каждая размером 1, которые должны быть сделаны в моменты . Одалживатель может сконструировать схему, показывая деление каждой выплаты на капитал и проценты.
Сразу после
й
выплаты остаётся
![]() неуплаченных выплат, и уравнение (3.7.5)
показывает, что неуплаченный заём –
просто
неуплаченных выплат, и уравнение (3.7.5)
показывает, что неуплаченный заём –
просто
![]() .
Таким образом
.
Таким образом
![]() . (1)
. (1)
Тогда
![]() .
(2)
.
(2)
Схема одалживателя может быть представлена
в форме таблицы (3.8.1). Более общё, если
сумма
одалживается при условии возврата в
выплат, каждая размером
![]() (???).
(???).
Таблица 1.
-
№ выплаты
процент
Capital repaid
заём, неуплаченный после выплаты
1
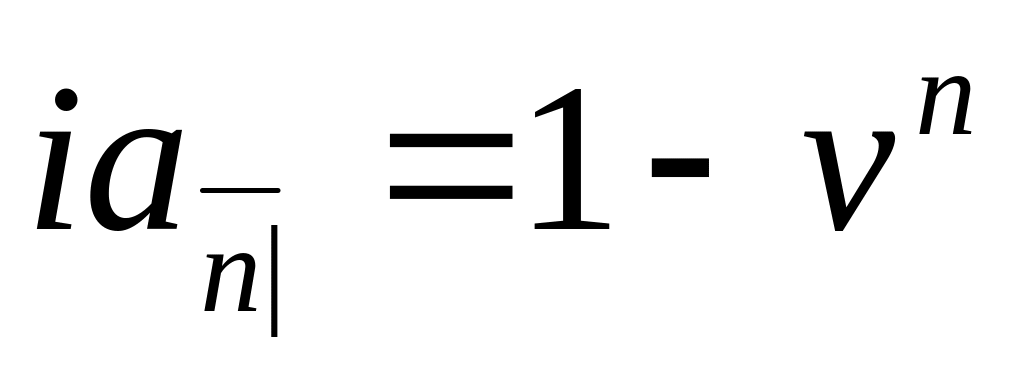
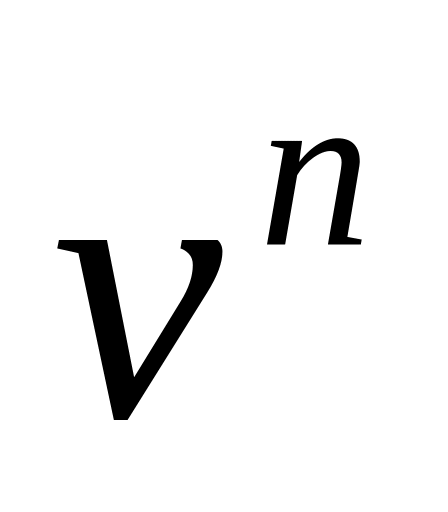
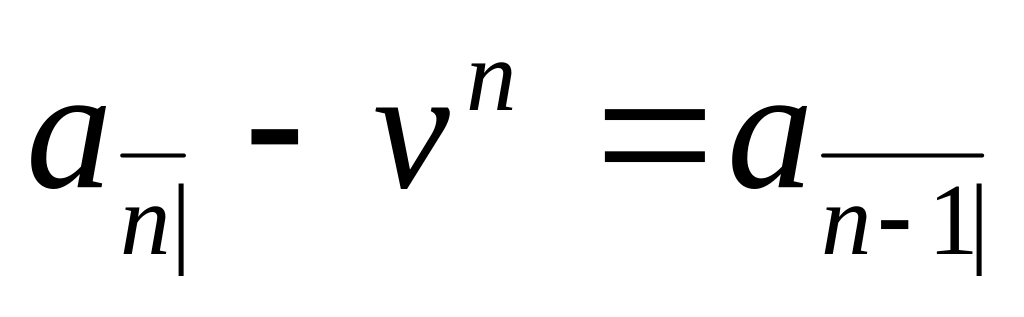
2
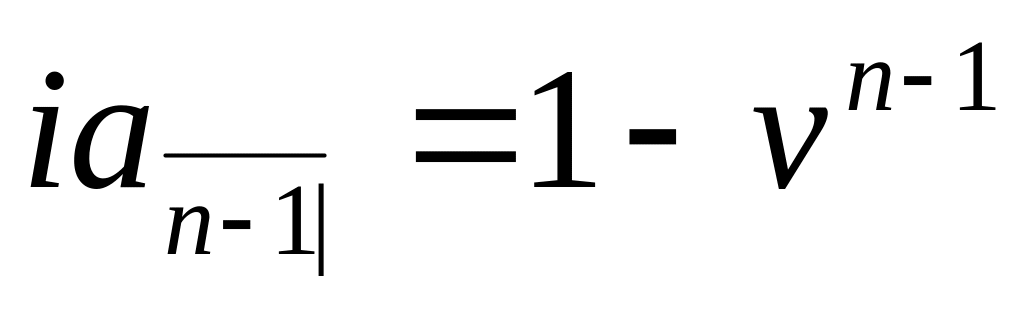
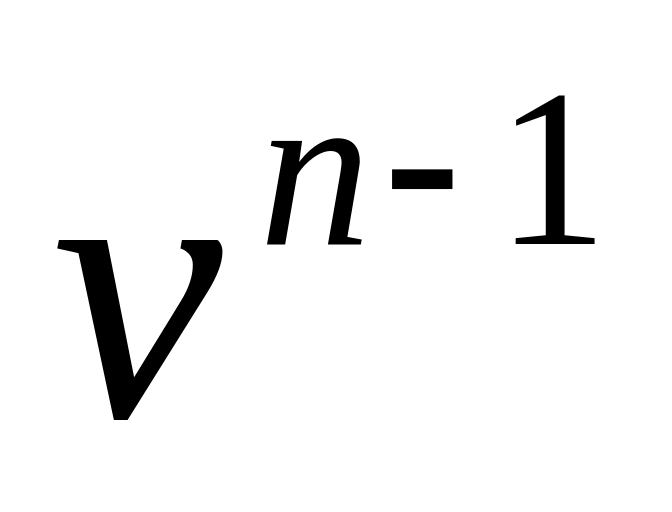
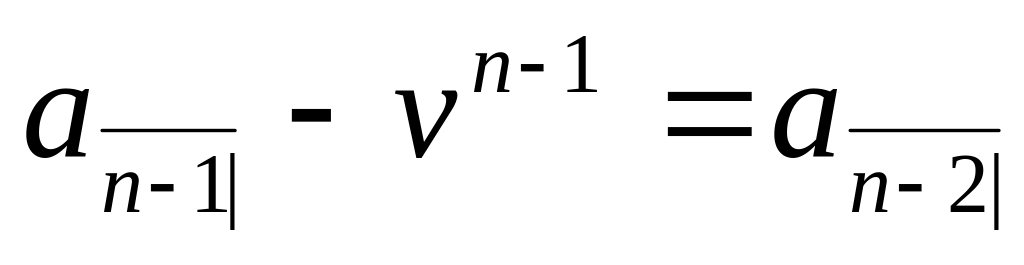
.
.
.
t
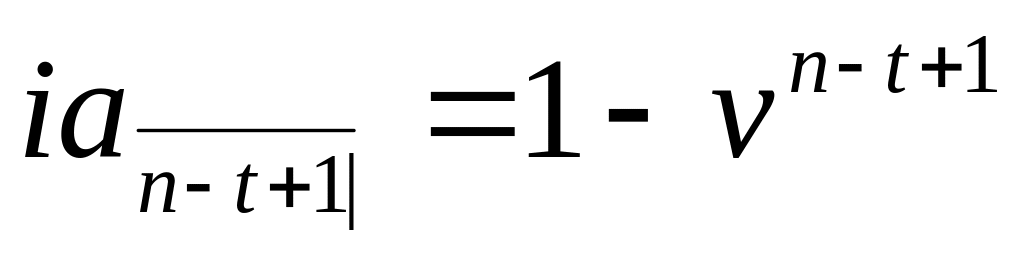
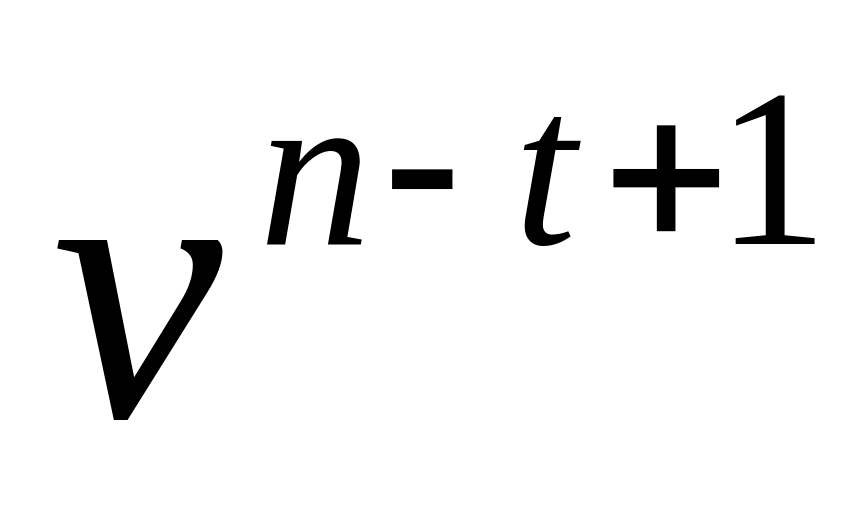
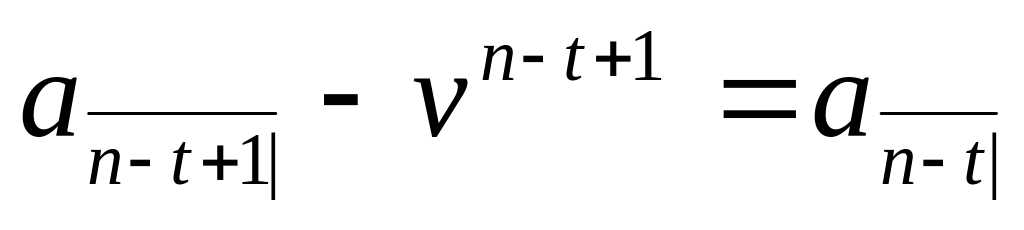
.
.
.
n-1
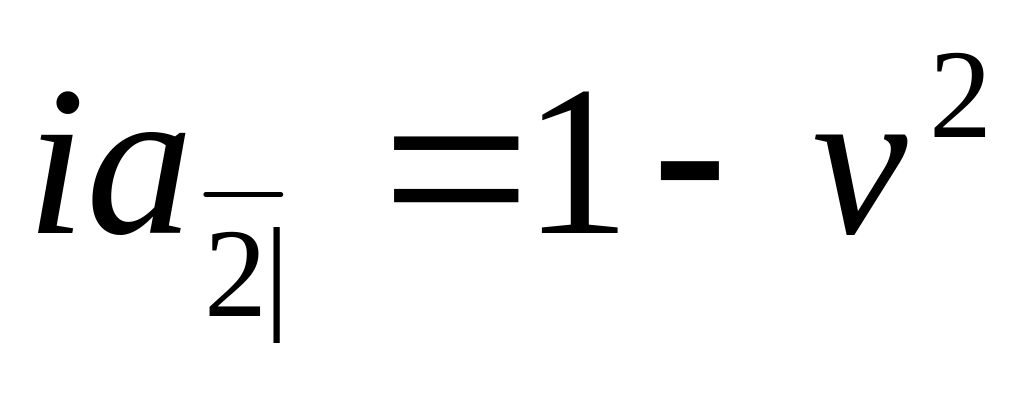
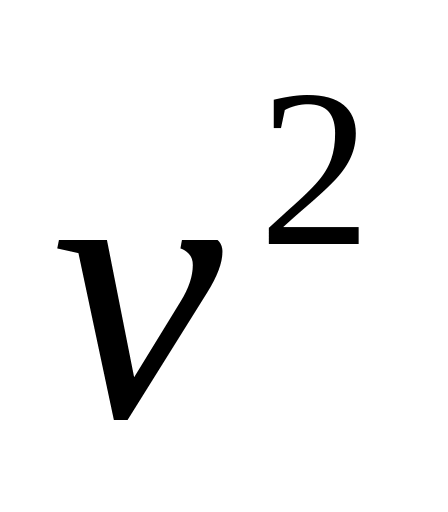
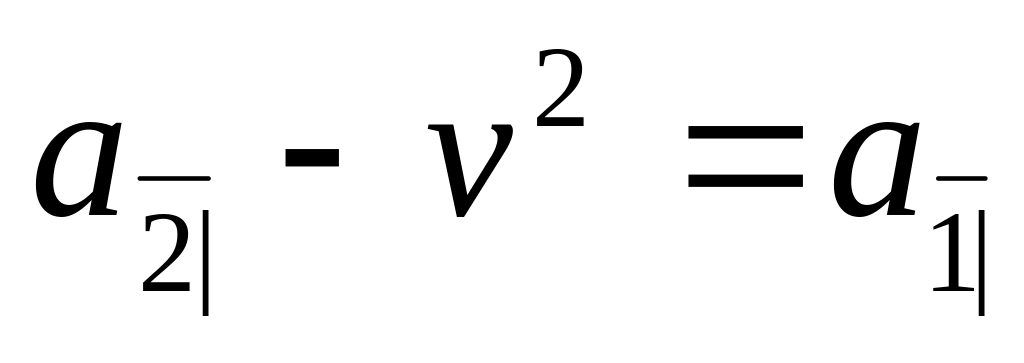
n
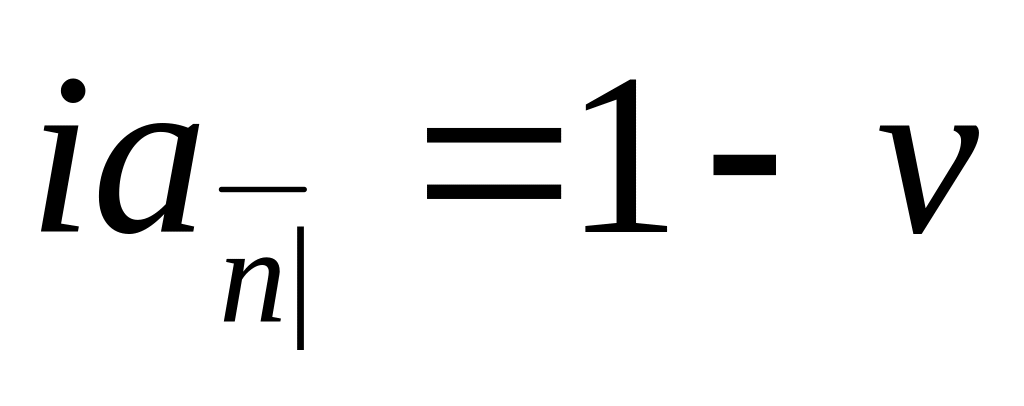
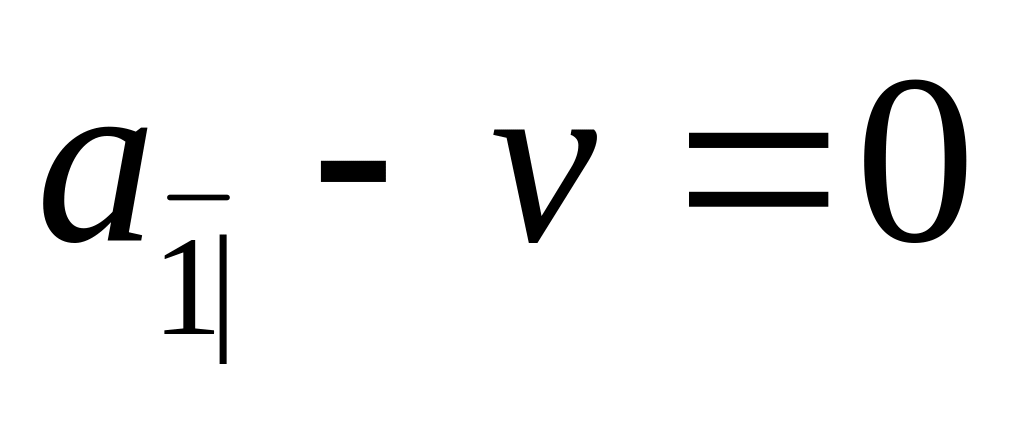
Если
![]() ,
то
,
то
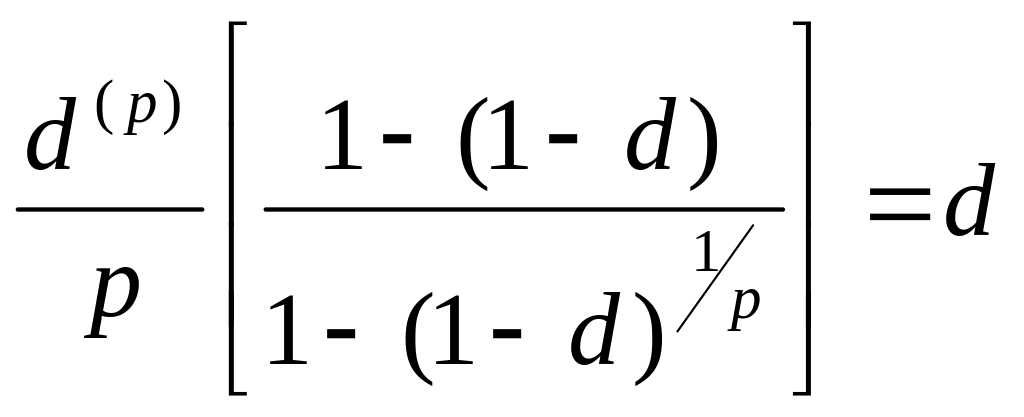
![]() (5)
(5)
![]() (6)
(6)
Заметим, что
![]() .
Полезны таблицы для
.
Полезны таблицы для
![]() .
Вставка.
.
Вставка.
Обычно на
и
![]() ссылаются как на номинальные ставки
процента и дисконта, конвертируемые
раз. Например, если мы говорим о ежегодной
конвертируемой поквартально ставке
процента 12%, то мы имеем
ссылаются как на номинальные ставки
процента и дисконта, конвертируемые
раз. Например, если мы говорим о ежегодной
конвертируемой поквартально ставке
процента 12%, то мы имеем
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Таким образом, эквивалентная ежегодная
эффективная ставка процента составляет
12,5509%. Когда процентные ставки выражаются
в номинальных терминах, эквивалентную
ежегодную ставку называют эффективной
ставкой. Таким образом, если номинальная
процентная ставка, конвертирующаяся
поквартально составляет 12%, то эффективная
ежегодная ставка составляет 12,5509%.
.
Таким образом, эквивалентная ежегодная
эффективная ставка процента составляет
12,5509%. Когда процентные ставки выражаются
в номинальных терминах, эквивалентную
ежегодную ставку называют эффективной
ставкой. Таким образом, если номинальная
процентная ставка, конвертирующаяся
поквартально составляет 12%, то эффективная
ежегодная ставка составляет 12,5509%.
На основе номинальной процентной ставки 12% ежегодно конвертируемой поквартально текущая стоимость 1 через лет составляет
![]()
Таким образом, если мы возьмём квартал в качестве единицы времени и используем 3% как эффективную процентную ставку, мы правильно оценим будущие выплаты.
Общее правило для номинальных ставок
очень просто. Выбираем за единицу времени
период соответствующий частоте, с
которой конвертируется номинальная
процентная ставка и используем
![]() как эффективную процентную ставку за
единицу времени. Например, если мы имеем
номинальную процентную ставку 18%,
конвертируемую ежемесячно, мы должны
взять 1 месяц за единицу времени и 1,5%
как эффективную процентную ставку за
единицу времени.
как эффективную процентную ставку за
единицу времени. Например, если мы имеем
номинальную процентную ставку 18%,
конвертируемую ежемесячно, мы должны
взять 1 месяц за единицу времени и 1,5%
как эффективную процентную ставку за
единицу времени.
Глава №4. Номинальные ставки процента. Ренты, выплачиваемые p раз.
§4.1 Процент, выплачиваемый p раз.
Предположим, что интенсивность процента за единицу времени постоянна и равна . Пусть и - ставка процента и дисконта соответственно.
В главе 3 мы показали, что
выплачивается в момент 0,
- в момент 1 и
выплачивается непрерывно в интервале
![]() по постоянной ставке, и все они имеют
одну и ту же стоимость. Каждый из этих
платежей может рассматриваться как
процент за период
,
выплачиваемый на заём 1, сделанный в
момент 0.
по постоянной ставке, и все они имеют
одну и ту же стоимость. Каждый из этих
платежей может рассматриваться как
процент за период
,
выплачиваемый на заём 1, сделанный в
момент 0.
Предположим, однако, что занимающий,
одолживший 1 в момент 0 для выплаты в
момент 1, желает платить процент по
своему займу в
платежей в интервале. Определим
- процент, выплачиваемый
раз в конце подинтервалов
![]() ;
- в начале подинтервалов
;
- в начале подинтервалов
![]() .
.
Мы можем выразить в терминах . Так как каждая процентная выплата равна , то
![]() . (1)
. (1)
Если
![]() ,
то
,
то
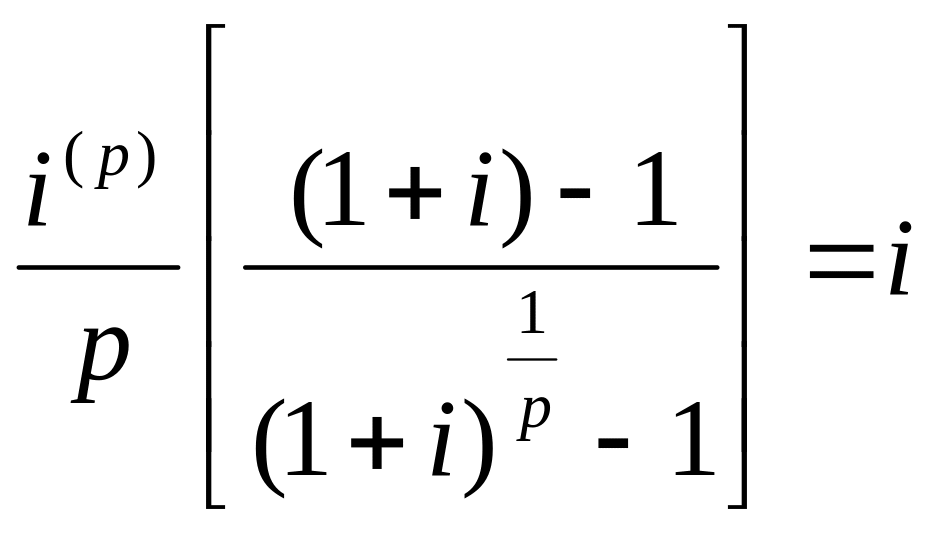 .
.
Следовательно
![]() и (2)
и (2)
![]() .
(3)
.
(3)
Уравнения (4.1.2) и (4.1.3) наиболее важны. Любые из уравнений может быть рассмотрено как определение . Аналогично
![]() .
(4)
.
(4)
Для интенсивности за единицу времени следующие 5 рядов выплат на временном интервале [0;1] имеют одну и ту же стоимость.
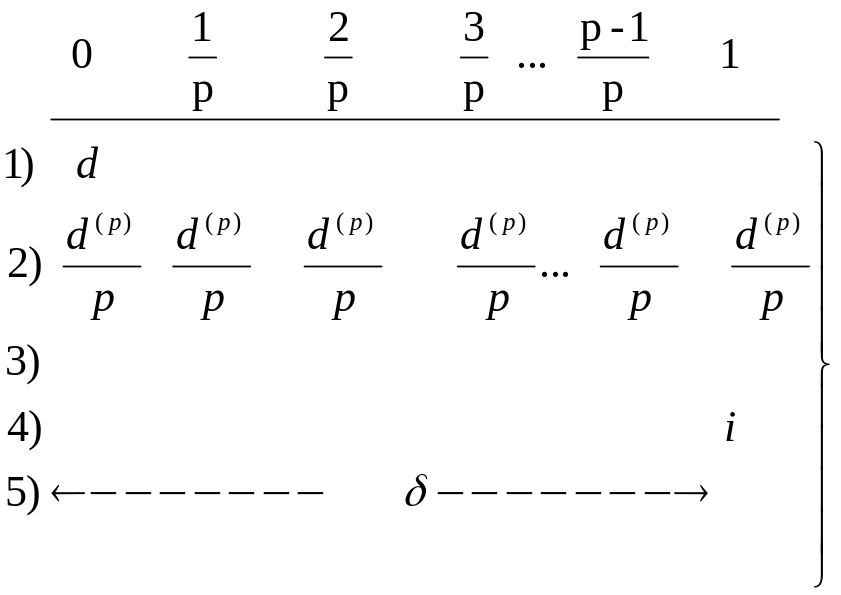
Заметим, что и задаются непосредственно в терминах интенсивности процента :
![]() (7)
(7)
Так как
![]() ,
то из (4.1.7)
следует
,
то из (4.1.7)
следует
![]() .
(8)
.
(8)
Легко установить, что
![]() ,
а
,
а
![]() .
Следовательно,
убывает при возрастании
,
а
возрастает при возрастании
.
.
Следовательно,
убывает при возрастании
,
а
возрастает при возрастании
.
Пример 4.1.4: Покажем, что если мало, то
![]() .
.
