§3.3 Ренты: текущие стоимости и накопления.

Рассмотрим ряд из платежей, каждый размером 1, которые должны быть сделаны через интервалы 1, платёж совершается в момент .

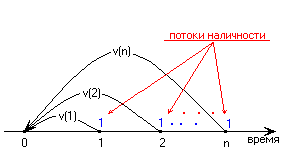
Стоимость этого ряда выплат в момент времени 0 называется настоящей (текущей) стоимостью и обозначается . Ясно, что если , то , иначе

(1)

Если , то . В рассмотренном случае первая выплата делается через 1 единицу времени от исходного момента 0, выплаты такого рода будем называть выплатами просрочкой.

Если же выплаты производятся в начале временных интервалов, то есть 1-я в момент и так далее, последняя в момент , то настоящая стоимость такого ряда выплат обозначается . Если , то , иначе

. (2)

Таким образом - стоимость в начале данного периода длины ряда из выплат, каждая по 1, которые делаются авансом на единичных интервалах на протяжении всего периода.

Из определения следует:

. (3)

Если выплаты производятся просрочкой, то стоимость ряда выплат на момент последней выплаты (в момент времени ) обозначается , если выплаты производились авансом, то их стоимость в момент обозначается .

Если , то , иначе

(4)

и

. (5)

Иногда и называются накоплением или накопленной суммой. Если , то и полагаются равными 0.

Из определения:

. (6)

Уравнения (3.3.1), (3.3.2), (3.3.4), (3.3.5) могут быть записаны в виде:

(7)

соответственно. (Первое уравнение представляет собой уравнение стоимости в момент на заём единичной суммы на период от 0 до , когда процент выплачивается в начале интервалов.) Для фиксированной величины - убывающие по функции, а - возрастающие по .

Для фиксированной ставки процента - возрастающие по функции. Когда , то рента называется пожизненной(вечной). Таким образом, если

(8)

(9)

Пример 3.3.1: Заём £2400 должен быть возвращён 20 равными ежегодными частями. Ставка процента на сделку 10% ежегодно. Найти сумму каждого ежегодного платежа, предполагая, что платежи делаются:

а) просрочкой;

б) авансом.

Решение:

а) Пусть ежегодный платёж составляет £ X. Тогда:

б) Пусть ежегодный платёж составляет £ Y. Тогда:

§3.4 Отсроченные ренты.

Предположим, что . Стоимость в момент ряда из выплат, каждая по 1, выплачиваемых в моменты обозначается . Иллюстрация этого случая:

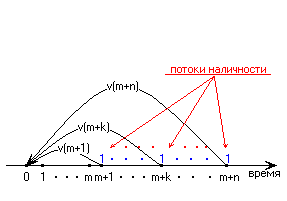
Такие серии выплат могут рассматриваться как срочная рента, отложенная на временных единиц.

Когда

. (1)

(2)

(3)

. (4)

Формула (3.4.1) может быть использована для любых , не только целых. В этом случае уравнение (3.4.3) будет тем же, но (3.4.2) и (3.4.4) – нет.

(5)

§3.5 Непрерывно выплачиваемые ренты.

Пусть . Стоимость в момент 0 ренты, которая может быть выплачена непрерывно между 0 и , где ставка (норма) выплат на единицу времени постоянна, обозначается .

, где (1)

Если , то .

Если , то для текущей стоимости непрерывно выплачиваемой ренты по 1 в единичный интервал времени на протяжении временных единиц и отложенной на временных единиц используется обозначение . Таким образом:

Следовательно

(2)

(3)

Уравнение (3.5.1) может быть записано в виде

.

Если целое, то