§2.5 Текущая стоимость (настоящая стоимость).

Пусть . Из (2.3.3) следует, что инвестиция размером в момент времени принесёт доход размером в момент времени . Говорят, что дисконтированной стоимостью в момент суммы в момент является величина

. (1)

То есть, это сумма денег, которая принесёт в момент , если её инвестировать в момент . В частности, дисконтированная стоимость в момент 0(текущий момент) суммы через время называется дисконтированной текущей стоимостью. Она равна

. (2)

Определим функцию

. (3)

Когда , тогда - дисконтированная текущая стоимость 1 через время . Когда , тогда преобразование

показывает, что - это накопление от момента до момента 0. Из (2.5.2) и (2.5.3) следует, что дисконтированная текущая стоимость суммы через время составляет

. (4)

Если , то

, (5)

где .

Пример 2.5.1: Единица измерения времени – год, и .

Найти простое выражение для , а также дисконтированную текущую стоимость $100 через 3,5 года.

Решение: Из (2.5.3):

.

Следовательно, дисконтированная текущая стоимость $100 из (2.5.4) составит

.

Пример 2.5.2: Предположим, что

.

Найти выражение для .

Решение: Для величину можно определить как , а для . Это даёт

.

§2.6 Формула Студли для интенсивности процента.

(1)

Параметры могут быть выбраны методами, описанными в §6.6. Если (2.6.1) справедлива, то:

(2)

Если определить , , то получим:

. (3)

Если формула Студли справедлива, то текущая стоимость любого потока наличности может быть выражена как взвешенное среднее двух фиксированных процентных ставок.

§2.7 Текущие стоимости потоков наличности.

Во многих задачах со сложными процентами требуется найти дисконти­ро­ван­ную стоимость выплат наличности или потоков наличности в буду­щем. Важно различать дискретные и непрерывные выплаты.

Дискретные потоки наличности.

Из (2.5.4) текущая стоимость сумм через время есть:

. (1)

Если ряд выплат есть бесконечный ряд, то текущая стоимость

(2)

(при условии, что ряд сходящийся). Процесс поиска дисконтированных текущих стоимостей можно проиллюстрировать на рисунке.

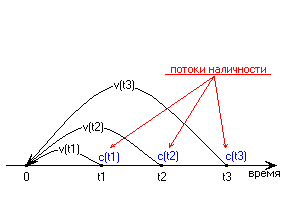
Дисконтирующие факторы используются, чтобы перенести выплаты наличности “назад в текущее время”.

Непрерывно выплачиваемые потоки наличности.

Этот случай важен, когда, например, пенсии выплачиваются еженедельно. Предположим, что и что между 0 и инвестор будет получать деньги непрерывно, а ставка выплаты в момент определяется функцией за единицу времени. Спрашивается, какова текущая стоимость этого потока наличности?

Для того, чтобы ответить на этот вопрос важно понять, что означает ставка выплаты потока наличности в момент . Если - общая выплата, сделанная между и , то, по определению,

. (3)

Тогда, если , то общая выплата, сделанная между и , составит:

. (4)

Таким образом, ставка выплаты – это производная общей суммы выплат к этому времени.

Между моментами времени и общая выплата составит . Если достаточно малое, то это . Следовательно, можно рассматривать текущую стоимость денег, полученных между и как . Текущая стоимость полного потока наличности получается интегрированием

. (5)

Если - бесконечность, то по аналогичным обстоятельствам текущая стоимость вычисляется по формуле:

. (6)

(2.7.5) является частным случаем (2.7.6), где для . Комбинируя результаты дискретного и непрерывного случаев, получаем:

(7)

для текущей стоимости общего потока наличности. Мы предполагали, что все выплаты положительны. Если имеется ряд входящих платежей (положительных) и ряд выходящих (отрицательных), то их чистая текущая стоимость определяется как разница между стоимостью положительного потока наличности и стоимостью отрицательного потока наличности.