§2.3 Факторы накопления.

Пусть время измеряется в разумных единицах (например, годах). Для определим - накопление в момент на инвестицию размером 1, сделанную в момент времени на срок . Таким образом, - это сумма, которая будет выплачена в момент в обмен на инвестицию размером 1 в момент времени . Из определения следует, что и

(1)

и, следовательно,

, . (2)

Из определения . Число называется аккумулирующим фактором, т.к. накопление в момент на инвестицию размером в момент есть

. (3)

Пусть . Рассмотрим инвестицию в момент . Если в момент инвестируется 1 на срок , то накопление (выручка, доход) в момент составит . Если же 1 инвестируется в момент на срок , а затем в момент доход реинвестируется на срок , то итог составит .

(Согласно принципу транзитивности???) Если выполняется принцип транзитивности, то

, . (4)

По индукции имеем

, и . (5)

Мы будем полагать, что принцип транзитивности выполняется, если не указано обратное. Однако на практике он не может быть реализован явно, из-за расходов, налогов и других факторов.

§2.4 Интенсивность процента.

Уравнение (2.3.2) указывает, как определяется в терминах аккумулирующего фактора . Предположим, что число такое, что

. (1)

Назовём интенсивностью процента за единицу времени в момент . Иногда называют номинальной процентной ставкой, конвертируемой мгновенно. Используя (2.3.2) и (2.4.1), определим в терминах аккумулирующего фактора:

. (2)

Теорема 2.4.1: Если и - непрерывные функции для , и принцип транзитивности выполняется, тогда для выполняется:

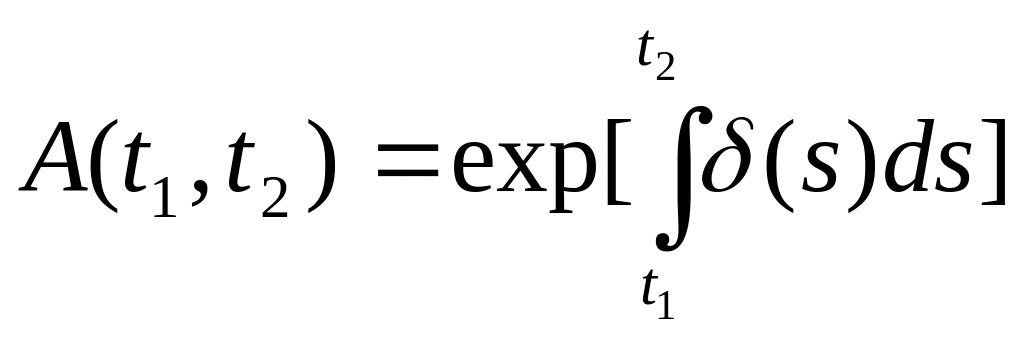. (3)

А также из (2.4.3) и (2.3.2) можно найти :

. (4)

Пример 2.4.1: Предположим, что:

а) ;

б) .

Найти формулы накопления от момента до момента для каждого случая.

Решение:

а) из (2.4.3) следует ;

б) .

Заметим, что когда , то

(5)

и . Из (2.4.4) следует, что эффективная процентная ставка за единицу времени

(6)

и, следовательно

, (7)

. (8)

Таким образом, получено обобщение формулы (2.1.2) .

Пример 2.4.2: Пусть . Время измеряется в годах.

Найти номинальную процентную ставку за год для депозита на срок

а) 7 дней;

б) 1 месяц;

в) 6 месяцев.

Решение:

Используя (2.4.4) с , получим

.

Подставляя: а) , б) , в) , получим номинальные процентные ставки: а) 12,01%, б) 12,06%, в) 12,37%.

Определим функцию

, (9)

где - фиксировано и . Таким образом, - накопление в момент на инвестицию размером 1 в момент . Из (2.4.3)

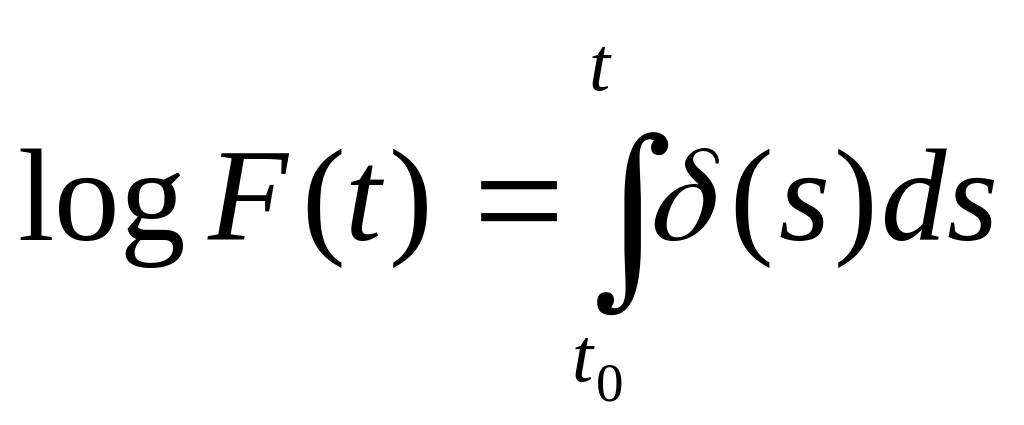(10)

и, следовательно, для

. (11)

Пример 2.4.3: Банковский процент по депозиту основывается на переменной интенсивности процента. 01.07.83г. клиент положил $50.000 на свой счёт в банке. На 01.07.85г. его депозит вырос до $59.102. Предполагая, что интенсивность процента - линейная функция по времени от 01.07.83г. до 01.07.85г., найти интенсивность процента на 01.07.84г.

Решение: Имеем и . Так как - линейная функция, то из (2.4.10) следует, что - квадратичная по для . Можно проверить, что для любой квадратичной функции и выполняется:

.

Тогда, используя (2.4.11), получим:

.

Мы предположили, что - непрерывная функция, но во многих практических задачах желательно рассмотреть более общую постановку. Часто - кусочно-постоянная функция. Например:

.

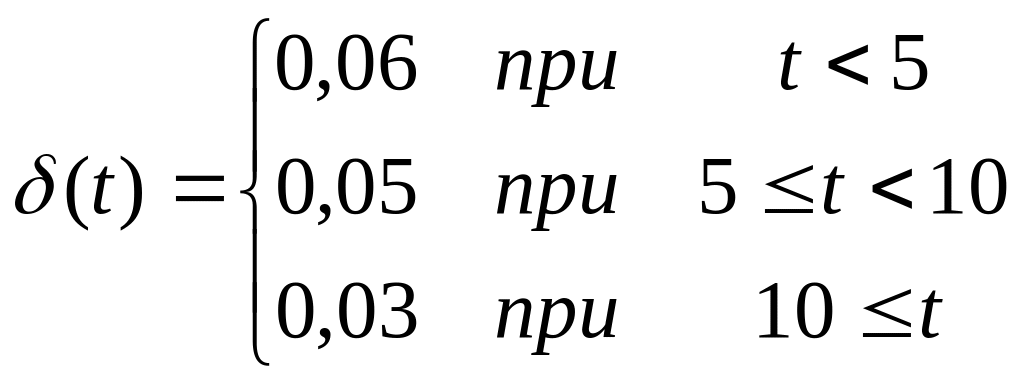Предыдущие результаты остаются справедливыми, а рассматриваем как предел последовательности непрерывных функций.