Глава №5. Дисконтированный поток наличности.

§5.1 Чистые потоки наличности.

Напомним (см. §3.2), что чистый поток наличности в момент (измеряется в разумных единицах времени) есть:

. (1)

Если любая выплата рассматривается как непрерывная, то чистая ставка потока наличности за единицу времени в момент определяется (см. гл. 3) по формуле:

,

где и - ставки дохода и расхода в момент соответственно.

Пример 5.1.1: Бизнесмен рассматривает определённый проект, связанный с магазином. Он оценивает, что предприятие будет расходовать вначале $2000, а через год ещё $10000. Оцениваемый доход $3000 ежегодно, выплачиваемый непрерывно в течение 10 лет, начиная с 3-го года, и окончательный доход $6000, когда проект закончится через 13 лет. Измеряемое время в годах, описать чистые потоки наличности, связанные со сделкой, и проиллюстрировать на диаграмме.

Решение: Мы имеем чистые потоки наличности:

, где .

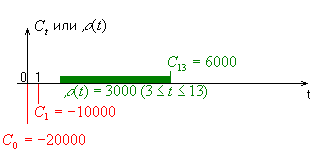
§5.2 Чистые текущие стоимости и доходы.

Имея достоверные или оценённые чистые потоки наличности на инвестиции или проект, инвестор желает измерить свою выгодность по отношению к другим возможным инвестициям или проектам. В особенности, он может пожелать определить благоразумно, или нет одолжение денег финансовой компании.

Предположим, что инвестор может одолжить, или занять деньги под фиксированную процентную ставку за единицу времени. Инвестор мог бы аккумулировать чистые потоки наличности, связанные с проектом, на отдельный счёт, на котором процент выплачивается или кредитуется по фиксированной ставке. Когда проект заканчивается (например, в момент ), баланс на этом счету будет

. (1)

Текущая стоимость по процентной ставке чистых потоков наличности называется чистой текущей стоимостью по процентной ставке на инвестиции и деловую сделку (проект) и обычно обозначается .

. (2)

Если , то

, (3)

где .

Так как

(4)

- это уравнение стоимости проекта в текущее время, доход на сделку есть решение этого уравнения при условии единственности.

Может быть показано, что - гладкая функция по и что при .

У экономистов ежегодным доходом часто называется внутренняя ставка на капитал ( ) или yield to redemtion.

Пример 5.1.1: Найти настоящую стоимость функции и доход на сделку в предыдущем примере. Построить график для при .

Решение: Из уравнения (5.2.2)

.

График:

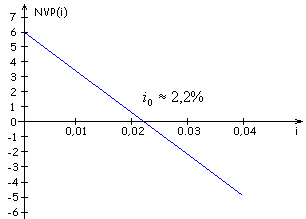
Практическая интерпретация и дохода – следующая: предположим, что инвестор может одолжить, или занять деньги по фиксированной процентной ставке . Так как (из уравнения (5.2.2)) - это текущая стоимость по процентной ставке чистого потока наличности, связанного с проектом, то мызаключаем, что проект будет выгодным только тогда, когда

. (5)

Также, если проект заканчивется в момент , выгода (или потеря) в этот момент времени есть (из уравнения (5.2.1)):

. (6)

??? Предположим, что при доходе существует и меняет знак с “+” на “-” при . При этих условиях ясно, что проект выгоден толбко тогда, когда

. (7)