
- •Актуарная математика. Глава №2. Теория процентных ставок.
- •§2.1 Ставка процента.
- •§2.2 Номинальная процентная ставка.
- •§2.3 Факторы накопления.
- •§2.4 Интенсивность процента.
- •§2.5 Текущая стоимость (настоящая стоимость).
- •Решение: Для величину можно определить как , а для . Это даёт
- •§2.6 Формула Студли для интенсивности процента.
- •§2.7 Текущие стоимости потоков наличности.
- •Дискретные потоки наличности.
- •Непрерывно выплачиваемые потоки наличности.
- •Пример 2.7.1: Пусть время измеряется в годах и
- •§2.8 Оцениваемые(valuing) потоки наличности.
- •§2.9 Процентный доход.
- •§2.10 Капитальные прибыли и убытки, налоги.
- •Глава №3.
- •§3.1 Основные функции сложных процентов.
- •§3.2 Уравнение стоимости и доход от сделки.
- •§3.3 Ренты: текущие стоимости и накопления.
- •§3.4 Отсроченные ренты.
- •§3.5 Непрерывно выплачиваемые ренты.
- •§3.6 Изменяющиеся ренты.
- •§3.7 Общая схема заёма.
- •§3.8 Схема заёма для level ренты.
- •Глава №4. Номинальные ставки процента. Ренты, выплачиваемые p раз.
- •§4.1 Процент, выплачиваемый p раз.
- •Решение:
- •Пример 4.1.3: Пусть и - положительные целые. Выразить в терминах . Найти когда . Решение: .
- •§4.2 Ренты, выплачиваемые p раз: текущие стоимости и накопления.
- •Глава №5. Дисконтированный поток наличности.
- •§5.1 Чистые потоки наличности.
- •§5.2 Чистые текущие стоимости и доходы.
- •§5.3 Сравнение двух инвестиционных проектов.
- •§5.4 Различные процентные ставки для заёмщиков и аккредиторов.
- •§5.5 Потоки инфляции.
- •§5.6 Доход фонда.
- •§5.7 Измерение инвестиционного performance.
Решение:
Аналогично

Пример 4.1.3: Пусть и - положительные целые. Выразить в терминах . Найти когда . Решение: .
Следовательно,
 и
и
 .
.

§4.2 Ренты, выплачиваемые p раз: текущие стоимости и накопления.
Если
и
- положительные целые,
![]() - стоимость в момент 0 ренты, выплачиваемой
раз по ставке 1 в единицу времени на
временном интервале [0;
].
Для этой ренты платежи делаются в моменты
времени
- стоимость в момент 0 ренты, выплачиваемой
раз по ставке 1 в единицу времени на
временном интервале [0;
].
Для этой ренты платежи делаются в моменты
времени
![]() ,
и сумма каждого платежа составляет
,
и сумма каждого платежа составляет
![]() .
.
По определению, ряд из
выплат, каждая по
,
в пределах
подинтервалов из любого единичного
интервала имеют ту же стоимость, что и
единственная выплата суммы
в конце единичного интервала. По
пропорции,
выплат, каждая суммой
в пределах
подинтервалов имеет ту же стоимость,
что и единственная выплата суммы
![]() в конце интервала.
в конце интервала.
Рассмотрим ренту, для которой текущая стоимость составляет .
Замечания предыдущего параграфа
показывают, что
выплат после момента
![]() и не позже момента
имеют ту же стоимость, что и выплата
единственной суммы
в момент
.
Это верно для
и не позже момента
имеют ту же стоимость, что и выплата
единственной суммы
в момент
.
Это верно для
![]() потому как рента имеет ту же стоимость,
как и ряд из
выплат, каждая размером
в моменты 1, 2, … ,
.
Это означает, что
потому как рента имеет ту же стоимость,
как и ряд из
выплат, каждая размером
в моменты 1, 2, … ,
.
Это означает, что
![]() .
(1)
.
(1)
Альтернативно, из первых принципов мы должны записать
 ,
(2)
,
(2)
что подтверждает (4.2.1).
Аналогично мы определим текущую
стоимость
![]() annuity-due, выплачиваемую
раз по ставке 1 в единицу времени на
временном интервале [0;
].
Платежи по ренте, каждый по
,
делаются в моменты
annuity-due, выплачиваемую
раз по ставке 1 в единицу времени на
временном интервале [0;
].
Платежи по ренте, каждый по
,
делаются в моменты
![]() .
Аналогично предыдущим рассуждениям:
.
Аналогично предыдущим рассуждениям:
![]() .
(3)
.
(3)
Из первых принципов имеем
![]() . (4)
. (4)
Заметим, что
![]() .
.
Комбинируя (4.2.1) и (4.2.3), получаем:
![]() .
(5)
.
(5)
Так как , то из (4.2.2) и (4.2.4) следует:
![]() .
.
Подобным образом определяем
![]() и
и
![]() - накопления, соответствующие
и
- накопления, соответствующие
и
![]() .
.
![]() (6)
(6)
![]() (7)
(7)
Выше приведённые пропорции могут быть применены и к другим рядам. Пусть, например, рента выплачивается ежегодно в течение лет, платеж за год составляет . Текущая стоимость этой ренты
![]() .
(8)
.
(8)
Рассмотрим другую ренту, также
выплачиваемую
лет с платежом
в год
,
но платежи делаются
раз в год. Если через
![]() обозначить текущую стоимость этой
ренты, заменяя
выплат для года
(каждая по
обозначить текущую стоимость этой
ренты, заменяя
выплат для года
(каждая по
![]() )
единственной эквивалентной выплатой
в конце года размером
)
единственной эквивалентной выплатой
в конце года размером
![]() ,
получим
,
получим
![]() ,
,
где
![]() - определяется (4.2.8).
- определяется (4.2.8).
Рента, выплачиваемая
раз в интервале, для которой платежи
продолжаются бесконечно, называется
вечно выплачиваемой
раз. Когда ставка постоянна и равна 1 за
единицу времени, то эта величина
обозначается
![]() .
Если платежи делаются авансом, то мы
имеем perpetuity-due
.
Если платежи делаются авансом, то мы
имеем perpetuity-due
![]() .
.
![]() (9)
(9)
Если в (4.2.2) и (4.2.4) получаем ( ):
![]() (10)
(10)
![]() . (11)
. (11)
Текущая стоимость, отложенная на временных единиц
![]() (12)
(12)
Заметим, что если
![]() ,
то
,
то
![]() соответственно равны
соответственно равны
![]() .
.
§4.3 Ренты, выплачиваемые на интервалах времени r, где r>1.
Предположим, что
![]() и
- целые числа большие 1, и рассмотрим ряд
выплат, каждая по
,
в моменты
и
- целые числа большие 1, и рассмотрим ряд
выплат, каждая по
,
в моменты
![]() .
Определим, какова стоимость этого ряда
выплат в момент 0 при процентной ставке
в единицу времени.
.
Определим, какова стоимость этого ряда
выплат в момент 0 при процентной ставке
в единицу времени.
Ситуация иллюстрируется рисунком:
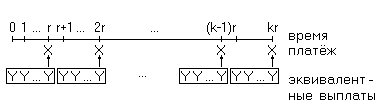
Заменим платёж
в момент
рядом из
платежей, каждый размером
![]() ,
в моменты
,
в моменты
![]() ,
где
выбирается так, чтобы сделать стоимость
этих
выплат равной стоимости единственного
платежа
.
,
где
выбирается так, чтобы сделать стоимость
этих
выплат равной стоимости единственного
платежа
.
Это означает, что
![]()
или
![]() . (1)
. (1)
Аналогично и далее. Тогда исходный ряд
выплат в
е
моменты времени по
каждая имеет ту же величину, что и ряд
![]() выплат по
в единичный временной интервал.
Следовательно, стоимость ренты составляет:
выплат по
в единичный временной интервал.
Следовательно, стоимость ренты составляет:
![]() .
(2)
.
(2)
Пример 4.3.1: Инвестор желает купить ренту в £120 в год, выплачиваемую поквартально в течение 5 лет. Найти цену покупки, если ставка процента 12% в год
а) эффективная;
б) конвертируемая раз в полгода;
в) конвертируемая поквартально;
г) конвертируемая ежемесячно.
Решение:
а) Стоимость
![]() ;
;
б) Так как ставка процента – номинальная, конвертируется раз в полгода, то мы имеем полгода в качестве единицы времени и 6% - ставка процента. Рента, выплачиваемая дважды за полгода для 10 полугодов по ставке £60 за полгода. Следовательно
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Пример 4.3.2: На основе эффективной
процентной ставки
,
строительное общество
![]() делает заём, который выплачивается
равными частями в конце года. Для любого
размера займа и срока выплаты строительное
общество
делает заём, который выплачивается
равными частями в конце года. Для любого
размера займа и срока выплаты строительное
общество
![]() просит такую же годовую выплату, что и
,
но требует, чтобы выплаты делались
просит такую же годовую выплату, что и
,
но требует, чтобы выплаты делались
![]() кратно
по факту (
кратно
по факту (![]() ).
Показать, что какой бы срок выплат не
был, эффективная процентная ставка за
год, получаемая
больше чем
).
Показать, что какой бы срок выплат не
был, эффективная процентная ставка за
год, получаемая
больше чем
![]() .
.
В частном случае, когда
![]() и
и
![]() ,
найти эффективную процентную ставку
за год на заём общества
,
когда срок
,
найти эффективную процентную ставку
за год на заём общества
,
когда срок
а) 10 лет;
б) 25 лет.
Решение: Пусть срок займа
лет и возвращаемая сумма
.
Ежегодная выплата для каждого общества
![]() ,
следовательно, эффективная процентная
ставка за год на заём общества
есть
,
где
,
следовательно, эффективная процентная
ставка за год на заём общества
есть
,
где
![]()
или
![]() ,
что определяет
.
,
что определяет
.
Левая часть этого уравнения – монотонно
убывающая функция
.
Поэтому для того, чтобы показать, что
его корень больше
,
достаточно показать, что когда
![]() ,
то левая часть уравнения больше правой.
Заметим, что
,
то левая часть уравнения больше правой.
Заметим, что
![]() .
.
Следовательно
 ,
,
так как
![]() .
.
![]() ,
что и требовалось доказать. Таким
образом,
,
что и требовалось доказать. Таким
образом,
![]() .
.
В частности это показывает, что если и , то эффективная процентная ставка за год на заём общества всегда больше, чем 8,3%.
