
- •2. Функции хеширования
- •2.1. Ключевые функции хеширования
- •2.2. Бесключевые функции хеширования
- •3. Электронная цифровая подпись
- •3 А. Схемы эцп с использованием дискретных логарифмов в простом конечном поле
- •Некоторые стандарты цифровой подписи
- •3 А.1. Федеральный стандарт сша.
- •3 А.2. Стандарт России – гост р34.10-94.
- •Введение
- •1 Область применения
- •2 Нормативные ссылки
- •3 Определения и обозначения
- •3.1 Определения
- •3.2 Обозначения
- •4. Общие положения
- •5. Математические соглашения
- •5.1. Математические определения
- •5.2. Параметры цифровой подписи
- •5.3. Двоичные векторы
- •6. Основные процессы
- •6.1. Формирование цифровой подписи
- •6.2. Проверка цифровой подписи
- •Приложение а (справочное) Дополнительные термины в области эцп
- •Приложение б (справочное) Контрольный пример
- •7B956de33814e95b7fe64fed924594dceab
- •Приложение в (справочное) Библиография*1
- •4. Режимы использования блочных шрифтов
5. Математические соглашения
Для определения схемы цифровой подписи необходимо описать базовые математические объекты, используемые в процессах ее формирования и проверки. В данном разделе установлены основные математические определения и требования, накладываемые на параметры схемы цифровой подписи.
5.1. Математические определения
Пусть задано
простое число
.
Тогда эллиптической
кривой
 ,
определенной над конечным простым
полем
,
называется множество пар чисел
,
определенной над конечным простым
полем
,
называется множество пар чисел
 ,
,
∈
,
удовлетворяющих тождеству
,
,
∈
,
удовлетворяющих тождеству

где
 и 4
и 4 не сравнимо с нулем по модулю
не сравнимо с нулем по модулю
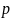 .
.
Инвариантом
эллиптической кривой называется величина
 , удовлетворяющая
тождеству
, удовлетворяющая
тождеству

Коэффициенты , эллиптической кривой Е , по известному инварианту , определяются следующим образом

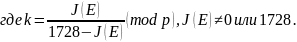
Пары
,
удовлетворяющие тождеству (1), называются
точками
эллиптической кривой
 ;
и
- соответственно
-
и
-координатами
точки.
;
и
- соответственно
-
и
-координатами
точки.
Точки эллиптической
кривой будем обозначать
 или просто
.
Две точки эллиптической кривой равны,
если равны их соответствующие х-
и у-координаты.
или просто
.
Две точки эллиптической кривой равны,
если равны их соответствующие х-
и у-координаты.
На множестве всех
точек эллиптической кривой
введем
операцию сложения, которую будем
обозначать знаком
 .
Для двух произвольных точек
.
Для двух произвольных точек
 и
и
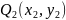 эллиптической
кривой
рассмотрим
несколько вариантов.
эллиптической
кривой
рассмотрим
несколько вариантов.
Пусть координаты
точек
 и
и
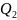 удовлетворяют условию
удовлетворяют условию
 .
В этом случае их суммой будем называть
точку
.
В этом случае их суммой будем называть
точку
 координаты
которой определяются сравнениями
координаты
которой определяются сравнениями

где

Если выполнены
равенства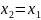 и
и 0, то определим координаты точки
0, то определим координаты точки
 следующим образом
следующим образом
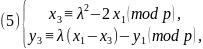
где

В случае, когда
выполнено условие
и
 сумму точек
и
;
будем называть нулевой
точкой О, не
определяя ее
-
и
-координаты.
В этом случае точка
называется отрицанием
точки
.
Для нулевой точки
сумму точек
и
;
будем называть нулевой
точкой О, не
определяя ее
-
и
-координаты.
В этом случае точка
называется отрицанием
точки
.
Для нулевой точки
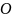 выполнены
равенства
выполнены
равенства
 ,
,
где − произвольная точка эллиптической кривой .
Относительно введенной операции сложения множество всех точек эллиптической кривой Е, вместе с нулевой точкой, образуют конечную абелеву (коммутативную) группу порядка m , для которого выполнено неравенство

Точка называется точкой кратности , или просто кратной точкой эллиптической кривой , если для некоторой точки выполнено равенство
 .
.
5.2. Параметры цифровой подписи
Параметрами схемы цифровой подписи являются:
− простое число
−
модуль эллиптической кривой, удовлетворяющее
неравенству
 . Верхняя граница данного числа должна
определяться при конкретной реализации
схемы цифровой подписи;
. Верхняя граница данного числа должна
определяться при конкретной реализации
схемы цифровой подписи;
− эллиптическая кривая , задаваемая своим инвариантом или коэффициентами
− целое число − порядок группы точек эллиптической кривой ;
− простое число − порядок циклической подгруппы группы точек эллиптической кривой , для которого выполнены следующие условия:
(9)

− точка
 эллиптической
кривой
, с координатами
эллиптической
кривой
, с координатами
 .
.
 )
, удовлетворяющая равенству
)
, удовлетворяющая равенству
 ;
;
− хэш-функция
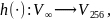 отображающая
сообщения, представленные в виде двоичных
векторов произвольной конечной длины,
в двоичные вектора длины
бит. Хэш-функция определена в ГОСТ Р
34.11.
отображающая
сообщения, представленные в виде двоичных
векторов произвольной конечной длины,
в двоичные вектора длины
бит. Хэш-функция определена в ГОСТ Р
34.11.
Каждый пользователь схемы цифровой подписи должен обладать личными ключами:
− ключом подписи
−
целым числом
, удовлетворяющим
неравенству
 ;
;
− ключом проверки
−
точкой эллиптической кривой
с координатами
 , удовлетворяющей равенству
, удовлетворяющей равенству

На приведенные выше параметры схемы цифровой подписи накладываются следующие требования:
− должно
быть выполнено условие
 для всех целых
для всех целых
 ,
где
,
где
 удовлетворяет
неравенству
удовлетворяет
неравенству
 ;
;
− должно быть
выполнено неравенство
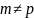 ;
;
− инвариант кривой
должен удовлетворять условию
 или
или
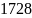 .
.
