5. Другие системы счисления

Троичная уравновешенная система счисления

В истории компьютерной техники применялись и другие системы счисления. Например, в 1958 г. была создана электронная вычислительная машина (ЭВМ) «Сетунь» (главный конструктор – Н.П. Брусенцов), которая использовала троичную систему счисления. Всего в 1960-х годах было выпущено более 50 промышленных образцов ЭВМ «Сетунь».

В троичной уравновешенной системе основание равно 3, используются три цифры: 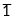(«минус 1»), 0 и 1. Один троичный разряд называется тритом (в отличие от двоичного бита). Система называется уравновешенной, потому что с помощью любого числа разрядов можно закодировать равное число положительных им отрицательных чисел, и число ноль. Вот, например, все двухразрядные числа

–4		= (–1)31 + (–1)30
–3	0	= (–1)31 + 030
–2	1	= рис. 2.33  (–1)31 + 130
–1	0	= 031 + (–1)30
0	0 0	= 031 + 030
1	0 1	= 031 + 130
2	1	= 131 + (–1)30
3	1 0	= 131 + 030
4	1 1	= 131 + 130

В последнем столбце этой таблицы числа записаны в развернутой форме, которую можно использовать для перевода из троичной уравновешенной системы в десятичную.

Заметьте, что положительные и отрицательные числа кодируются с помощью одних и тех же правил. Это большое преимущество в сравнении с двоичным кодированием, при котором для хранения отрицательных чисел пришлось изобретать специальный код.

Троичная уравновешенная система счисления дает ключ к решению задачи Баше, которая была известна еще в XIII веке Леонардо Пизанскому (Фибоначчи):

Найти такой набор из 4 гирь, чтобы с их помощью на чашечках равноплечных весов можно было взвесить груз массой от 1 до 40 кг включительно. Гири можно располагать на любой чашке весов.

Каждая гиря может быть в трех состояниях:

1. лежать на той же чашечке весов, что и груз: в этом случае ее вес вычитается из суммы ( );

2. не участвовать во взвешивании (0);

3. лежать на другой чашке: ее вес добавляется к сумме (1).

Поэтому веса гирь нужно выбрать равными степеням числа 3, то есть 1, 3, 9 и 27 кг.

Двоично-десятичная система счисления

Существует еще один простой способ записи десятичных чисел с помощью цифр 0 и 1. Этот способ называется двоично-десятичной системой (ДДС), это нечто среднее между двоичной и десятичной системами. На английском языке такое кодирование называется binary coded decimal (BCD) – десятичные числа, закодированные двоичными цифрами.

В ДДС каждая цифра десятичного числа записывается двоичными знаками. Но среди цифр 0–9 есть такие, которые занимают 1, 2, 3 и 4 двоичных разряда. Чтобы запись числа была однозначной, и не надо было искать границу между цифрами, на любую цифру отводят 4 бита. Таким образом, 0 записывается как 0000, а 9 – как 1001. Например:

9024,19 = 1001 0000 0010 0100, 0001 1001 _ДДС

9 0 2 4 1 9

При обратном переводе из ДДС в десятичную систему надо учесть, что каждая цифра занимает 4 бита, и добавить недостающие нули:

101010011,01111_ДДС = 0001 0101 0011, 0111 1000 _ДДС = 153,78

Важно помнить, что запись числа в ДДС не совпадает с его записью в двоичной системе:

10101,1_ДДС = 15,8

10101,1₂ = 16 + 4 + 1 + 0,5 = 21,5

Использование ДДС дает следующие преимущества:

• двоично-десятичный код очень легко переводить в десятичный, например, для вывода результата на экран;

• просто выполняется умножение и деление на 10, а также округление;

• конченые десятичные дроби записываются точно, без ошибки, поэтому вычисления в ДДС (вместо двоичной системы) дадут тот же результат, что и ручные расчеты человека «на бумажке»; поэтому ДДС используется в калькуляторах.

Есть, однако, и недостатки:

• хранение чисел в ДДС требует больше памяти, чем стандартный двоичный код;

• усложняются арифметические операции.

Задачи

1. Как представлено число 83₁₀ в двоичной системе счисления?

1) 1001011₂ 2) 1100101₂ 3) 1010011₂ 4) 101001₂

2. Сколько единиц в двоичной записи числа 195?

1) 5 2) 2 3) 3 4) 4

3. Сколько единиц в двоичной записи числа 173?

1) 7 2) 5 3) 6 4) 4

4. Как представлено число 25 в двоичной системе счисления?

1) 1001₂ 2) 11001₂ 3) 10011₂ 4) 11010₂

5. Как представлено число 82 в двоичной системе счисления?

1) 1010010₂ 2) 1010011₂ 3) 100101₂ 4) 1000100₂

6. Как представлено число 263 в восьмеричной системе счисления?

1) 301₈ 2) 650₈ 3) 407₈ 4) 777₈

7. Как записывается число 567₈ в двоичной системе счисления?

1) 1011101₂ 2) 100110111₂ 3) 101110111₂ 4) 11110111₂

8. Как записывается число A87₁₆ в восьмеричной системе счисления?

1) 435₈ 2) 1577₈ 3) 5207₈ 4) 6400₈

9. Как записывается число 754₈ в шестнадцатеричной системе счисления?

1) 738₁₆ 2) 1A4₁₆ 3) 1EC₁₆ 4) A56₁₆

10. Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-128)?

1) 1 2) 2 3) 3 4) 4

11. Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-35)?

1) 3 2) 4 3) 5 4) 6

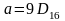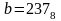12. Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

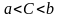1) 10011010₂ 2) 10011110₂ 3) 10011111₂ 4) 11011110₂

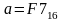13. Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11111001₂ 2) 11011000₂ 3) 11110111₂ 4) 11111000₂

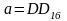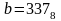14. Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11011010₂ 2) 11111110₂ 3) 11011110₂ 4) 11011111₂

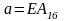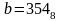15. Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11101010₂ 2) 11101110₂ 3) 11101011₂ 4) 11101100₂

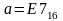16. Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11101010₂ 2) 11101000₂ 3) 11101011₂ 4) 11101100₂

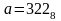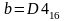17. Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11010011₂ 2) 11001110₂ 3) 11001010₂ 4) 11001100₂

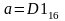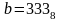18. Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11100011₂ 2) 11011010₂ 3) 10101101₂ 4) 11011101₂

19. Сколько единиц в двоичной записи числа 64?

1) 1 2) 2 3) 4 4) 6

20. Сколько единиц в двоичной записи числа 127?

1) 1 2) 2 3) 6 4) 7

1 При 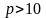используются также и латинские буквы, но об этом далее.