Тема 2. Виды относительных величин и формулы для их расчета:

1. Процент планового задания характеризует планируемое изменение показателя по сравнению с фактически достигнутым в период, предшествующий плановому:

% пл. зад. ,

где - плановый уровень;

- базовый уровень или уровень периода, предшествующего плановому.

2. Процент выполнения плана характеризует степень выполнения плана (прогноза):

% в.п. ,

где - фактический уровень, достигнутый в анализируемом периоде.

3. Коэффициент динамики (роста) характеризует изменение явления во времени:

а) базисный ; б) цепной ,

где = - фактический уровень, достигнутый в анализируемом периоде;

- уровень, предшествующий текущему (анализируемому) периоду.

4. Удельный вес - относительная величина структуры совокупности (это часть от целого):

,

где - объем части изучаемой совокупности;

- общий объем совокупности.

5. Коэффициент координации характеризует соотношение между отдельными частями изучаемой совокупности, одна из которых принимается за базу сравнения:

,

где - часть сравниваемой совокупности;

- часть совокупности, принятой за базу сравнения.

6. Относительная величина сравнения характеризует соотношение одноименных показателей, относящихся к различным объектам или территориям, но за один и тот же период:

,

где - объем сравниваемой совокупности;

- объем совокупности, принятый за базу сравнения.

7. Относительная величина интенсивности характеризует распространенность данного явления в определенной среде. В основном это соотношение двух разноименных абсолютных величин. Применяется для характеристики уровня развития явления (сколько единиц числителя приходится на 1, 100, 1000 и т.д. единиц знаменателя). К показателям интенсивности относят коэффициент рождаемости, смертности, самоубийств, преступности.

Тема 3. Средние величины

Средняя величина - это обобщающая характеристика изучаемой статистической совокупности по какому-либо признаку. Наиболее распространенными средними величинами являются: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя хронологическая, средняя геометрическая (см. тему 5: "Ряды динамики", расчет среднего темпа роста).

Выбор формулы расчета средней величины зависит только от вида исходных данных. Средняя арифметическая применяется, если известны значения осредняемого признака Х и число единиц совокупности с этим значением X. Если каждая варианта - Х встречается 1 раз, то применяется средняя арифметическая простая:

где - число единиц совокупности.

Средняя арифметическая простая, как правило, применяется, если исходные данные не упорядочены. Если каждая варианта - Х встречается несколько раз, то применяется средняя арифметическая взвешенная:

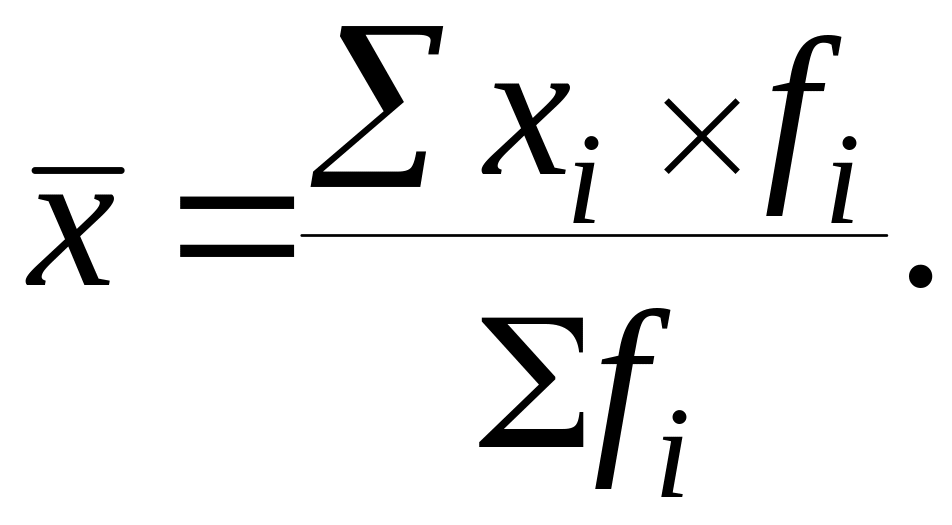
где - частота признака.

Средняя арифметическая взвешенная применяется, если задан упорядоченный ряд распределения.

Пример 1: Построить дискретный ряд распределения студентов по возрасту и вычислить среднюю арифметическую взвешенную. Дать характеристику группировке.

Возраст	Кол-во чел.	Возраст	Кол-во чел.	Возраст	Кол-во чел.
22	5	29	3	37	2
23	3	30	6	38	2
24	4	31	3	39	1
25	1	32	3	40	1
26	4	33	1	46	1
27	2	34	4	50	1
28	1	36	2

Решение: лет.

Характеристика группировки: вариационная, дискретная, однофакторная, первичная, структурная.

Построить интервальный ряд распределения и произвести расчет средней по интервальному ряду.

Алгоритм расчета: 1) Закрыть открытые интервалы, приняв их равными ближайшему закрытому. 2) За значение Х взять середину каждого интервала (значение первого + значение последнего и поделить на 2); 3) Провести расчет средней арифметической взвешенной.

Возраст	Середина интервала
До 25 лет	23	13	299
26 - 30 лет	28	16	448
31 - 35 лет	33	11	363
36 и более	38	10	380

Решение: лет.

В статистике приходится вычислять средние по вариантам, которые являются групповыми (частными) средними. В таких случаях общая средняя определяется как средняя арифметическая взвешенная из групповых средних, в которых весами являются объемы единиц в группах.

Пример 2: Задолженность по кредитам предприятий за отчетный период характеризуется следующими данными:

№ предприятия	Задолженность по кредитам, тыс.руб.,	Удельный вес просроченной задолженности, %,	Объем просроченной задолженности, тыс.руб.,
1	2500	20	500
2	3000	30	900
3	1000	16	160
ИТОГО	6500	-	1560

Определите средний процент просроченной задолженности по кредитам предприятий.

Решение: Экономическое содержание показателя равно:

Удельный вес задолженности =	Объем просроченной задолженности	100, %
	Объем общей задолженности

Для расчета среднего процента просроченной задолженности надо сравнить суммарные показатели просроченной задолженности и общей задолженности предприятий. Применяем формулу средней арифметической взвешенной:

Средняя гармоническая

Средняя гармоническая применяется, когда неизвестна частота ( ), но известны произведения варианты (X) на частоту ( ), то есть . Средняя гармоническая вычисляется из обратных значений осредняемого признака и по форме может быть простой и взвешенной.

Средняя гармоническая простая:

где - число единиц совокупности.

Средняя гармоническая взвешенная:

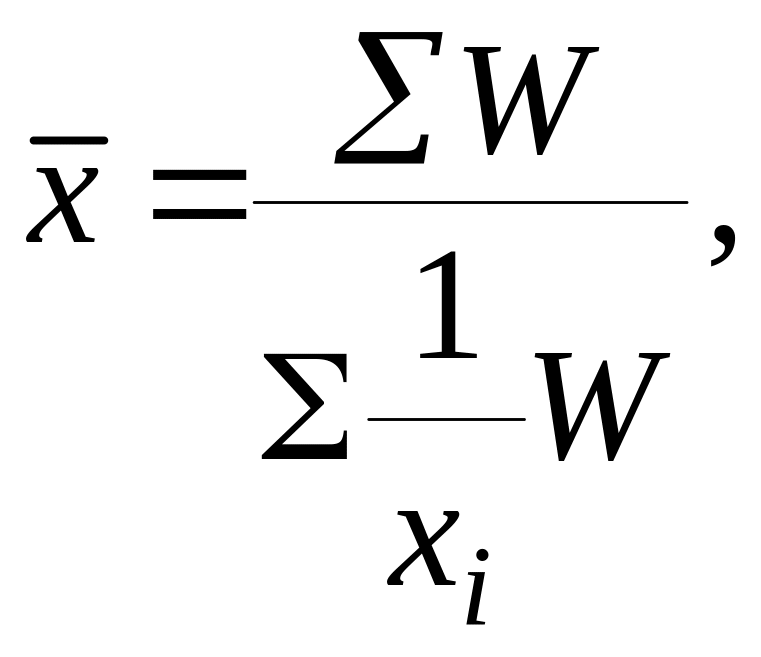где .

Пример 1: Доходы банков в отчетном году характеризуются следующими показателями:

№ банка	Средняя процентная ставка X	Доход банка, тыс.руб. Д=	Сумма кредита, тыс.руб. Д / X
1	40	600	1500
2	35	350	1000
ИТОГО	-	950	2500

Определите среднюю процентную ставку банков.

Решение: Основой выбора средней является реальное содержание определяемого показателя:

Ставка =	Доход банка	 100, %
	Сумма кредита

В задаче отсутствуют прямые данные о кредитах, но их суммы можно определить расчетным путем, разделив доход банка (Д) на процентную ставку ( ) (см. последнюю графу).

Среднюю процентную ставку определяем по формуле средней гармонической взвешенной. Веса представляют собой произведения процентной ставки ( ) на сумму кредита ( ): Д= .

Средняя хронологическая

Средняя хронологическая применяется когда значения признака Х заданы на несколько дат внутри периода. Формула средней хронологической:

,

где, - число дат, на которые известны значения Х.

Пример 1: Остатки денежных средств на расчетном счете предприятия (в т.руб.) характеризуются следующими данными:

Дата	01.01	01.02	01.03	01.04	01.05	01.06	01.07
Остаток	175	190	215	255	320	370	460

Определить: среднедневное наличие денег на расчетном счете за 1-ый квартал, 2-ой квартал и за 1-е полугодие.

За первый квартал: т. руб.

За второй квартал: т. руб.

За полугодие:

т. руб.

Выводы:

1) в первом квартале ежедневно находилось денег на расчетном счете в сумме 206,7тыс. руб.

2) во втором квартале ежедневно находилось денег на расчетном счете в сумме 349,2тыс. руб.

3) в первом полугодии ежедневно находилось денег на расчетном счете в сумме 277,9тыс. руб.

Для изучения внутреннего строения совокупности применяют структурные средние - моду и медиану. По имеющимся данным интервального вариационного ряда нужно исчислить моду, медиану, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.

Мода ( ) - наиболее часто встречающееся значение признака в совокупности. В дискретном ряду мода определяется по наибольшей частоте. Для интервального ряда с равными интервалами мода определяется по формуле:

,

где - нижнее значение модального интервала (имеющего наибольшую частоту);

- ширина (шаг) интервала;

- частота модального интервала;

и - соответственно: частота интервала, предшедствующего (последующего) модальному.

Медиана ( ) - середина ранжированного ряда, т.е. величина признака, делящая ряд на две равные части. Для дискретного с нечетным числом уровней медианой будет варианта, находящаяся в середине ряда:

,

где – номер медианы.

Для дискретного ряда с четным числом медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда:

.

Для интервального вариационного ряда медиана определяется по формуле:

,

где - нижняя граница медианного интервала;

- его величина; - его частота;

-сумма накопленных частот в интервалах, предшествующих медианному;

- сумма частот ряда.

Не каждая средняя величина является объективной характеристикой изучаемой совокупности. Для расчета типичности средней, колеблемости признака применяются показатели вариации.