14. Адіабатний процес та його рівняння. Робота в адіабатному процесі.
14.1. Адіабатичний процес. Рівняння Пуасона
Адіабатичним
(або адіабатним) називається процес, що
протікає без теплообміну з навколишнім
середовищем. Умова такого процесу:
(або Q=0). Застосовуючи до адіабатичного
процесу 1-й принцип термодинаміки (2.29),
маємо
,
(2.39)
тобто при адіабатичному розширенні газ виконує роботу за рахунок запасу його внутрішньої енергії. При цьому ідеальний газ охолоджується. Дійсно, взявши до уваги вираз для внутрішньої енергії (2.37), маємо
. (2.40)
Звідси
бачимо, що при розширенні газу (A>0)
приріст температури
,
в чому і треба було переконатися. Описане
явище – спосіб отримання низьких
температур.
Вираз (2.40) дозволяє розрахувати роботу ідеального газу при адіабатичному процесі. Якщо використати рівняння Менделєєва-Клапейрона, то цю роботу можна виразити через параметри p та V.
Щоб здійснити адіабатичний процес, треба надійно теплоізолювати систему або здійснювати його дуже швидко, щоб теплообмін практично не встигав відбутися. Другий з цих варіантів зустрічається у природі. Наприклад, величезні маси атмосферного повітря, нагріваючись біля поверхні Землі, піднімаються вгору, потрапляють в області нижчих тисків і розширюються. Цей процес адіабатичний, бо через погану теплопровідність повітря теплообміном при цьому можна знехтувати. Виконуючи роботу розширення проти зовнішнього тиску, повітря охолоджується, а водяна пара перетворюється в насичену й конденсується (хмари).
Згущення і розрідження, що утворюються у звуковій хвилі в газах, – це також по суті процеси адіабатичного стиснення і розширення газу. Оскільки швидкість поширення звуку немала (340м/с при кімнатних температурах), процеси тут відбуваються так швидко, що за цей короткий час теплообміном можна знехтувати.
Приступимо тепер до виведення рівняння адіабати. За основу беремо вираз 1-го принципу термодинаміки для цього процесу (в диференціальній формі (2.30)):
.
(2.41)
Розпишемо ліву частину цього рівняння. Елементарну роботу розрахуємо на основі формули (2.25), причому тиск підставимо, взявши його з рівняння Менделєєва-Клапейрона (2.3):
.
Елементарний приріст внутрішньої енергії dU запишемо, продиференціювавши вираз (2.37):
.
Тепер замість (2.41) маємо
.
Поділимо
далі останнє рівняння на добуток
і одержимо
.
(2.42)
Коефіцієнт
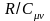запишемо, виразивши газову сталу через
різницю
з рівняння Майєра (2.38):
,
де введено позначення
.
(2.43)
Тепер співвідношення (2.42) приймає вигляд
.
Оскільки
,
то наше рівняння запишеться у формі
або
.
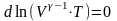Звідси випливає, що
Або
.
(2.44)
С
Рис. 2.9
піввідношення (2.44) є рівнянням адіабати або рівнянням Пуасона. Параметр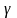
,
введений вище, називається показником
адіабати або коефіцієнтом Пуасона. Для
повітря, наприклад,
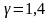(в сухому повітрі 99% двохатомних молекул!).
В загальному випадку
,
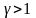оскільки
.
Визначаючи абсолютну температуру з рівняння Менделєєва-Клапейрона і підставляючи одержаний вираз у співвідношення (2.44), одержимо іншу форму запису рівняння Пуасона:
.
(2.45)
Згадаємо,
що рівняння ізотерми
.
Порівняння двох останніх виразів
приводить до висновку, що адіабата
графічно “крутіша” від ізотерми (див.
рис.2.9).
Якщо з рівняння Менделєєва-Клапейрона або з рівняння (2.45) визначити об’єм V і підставити одержаний вираз у (2.44), то матимемо третю форму запису рівняння Пуасона
.
(2.46)
Зауваження: 1) рівняння Пуасона (2.44–46) правильні за умови, що кількість газу (чи його маса) незмінні під час процесу; 2) величини “const” у всіх виписаних рівняннях різні.
………………………………………………………………………………………………………………..