31. Дифракція Фраунгофера на щиліни та решітці

Дифракцією Фраунгофера називається дифракція плоских хвиль (паралельних променів). Дифракція Фраунгофера має більше практичне значення, ніж дифракція Френеля (дифракція сферичних хвиль).

Р

Рис.6.15

озглянемо довгу прямокутну щілину BС шириною a, на яку нормально падає паралельний пучок монохроматичного світла (рис.6.15). Згідно з принципом Гюйгенса-Френеля, точки щілини є когерентними вторинними джерелами, що породжують коливання в одній фазі (площина щілини співпадає з фронтом хвилі).

За допомогою лінзи Л на екрані Е спостерігається дифракційна картина, яка є системою максимумів і мінімумів. Знайдемо умови спостереження максимумів і мінімумів. Для цього розіб’ємо фронт хвилі ВС на зони Френеля таким чином, щоб оптична різниця ходу від країв сусідніх зон у певному напрямку поширення дифрагованої хвилі під кутом дифракції  складала половину довжини хвилі . З рис.6.15 видно, що ширина зони Френеля дорівнює . Якщо число зон парне, то

(6.31)

і під кутом  спостерігається дифракційний мінімум. Коливання від відповідних точок сусідніх зон у точці спостереження відбуваються у протифазі, тому випромінювання від сусідніх зон в цілому взаємно компенсуються.

Якщо число зон непарне, то

(6.32)

то спостерігається дифракційний максимум, який відповідає дії однієї нескомпенсованої зони Френеля. Величина m називається порядком дифракційного максимуму (мінімуму).

Амплітуда хвилі в точці спостереження одержується на основі принципу Гюйгенса-Френеля:

(6.33)

де – амплітуда в центрі дифракційної картини при .

Р

Рис. 6.16

озподіл інтенсивностей :

(6.34)

Цей розподіл показаний на рис. 6.16.

Перейдемо до дифракції на одновимірній дифракційній решітці, що є системою N однакових паралельних щілин шириною а, розміщених на однакових відстанях b. Величина називається періодом решітки. Сучасна дифракційна решітка має 1200 і більше щілин (штрихів) на 1мм.

Дифракційна картина після решітки складніша порівняно з картиною від однієї щілини. Це зумовлене тим, що відбувається інтерференція хвиль, які йдуть від різних щілин решітки, тому має місце підсилення максимумів і їх звуження.

Якщо світло падає нормально на решітку, то виконуються такі умови:

для головних максимумів: ; (6.35)

для головних мінімумів: ; (6.36)

для додаткових мінімумів: (6.37)

(k–довільні цілі додатні числа, крім 0, N, 2N, 3N, …).

Розподіл інтенсивності на екрані спостереження:

(6.38)

де 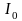–інтенсивність в напрямку для однієї щілини. В головних максимумах інтенсивність світла в разів більша від інтенсивності відповідних максимумів дифракційної картини від однієї щілини. При великому значенні N вторинні максимуми майже непомітні на екрані, їх інтенсивність не більша 5% від інтенсивності головного максимуму.

На рис.6.17 показана дифракційна картина після дифракційної решітки в білому світлі (вторинні максимуми не зображені). З умови головних максимумів випливає, що для всіх порядків, крім m = 0, біле світло розкладається в спектр. Тому дифракційна решітка використовується як диспергуючий елемент в спектрометрах.

В

Рис.6.17

ажливою характеристикою оптичних приладів є їхня роздільна здатність. Згідно з критерієм Релея, зображення двох близьких точок можна вважати розділеними, якщо центральний дифракційний максимум від однієї точки співпадає з першим дифракційним мінімумом для другої точки.

Для круглого отвору роздільна здатність

(6.39)

де D – діаметр отвору,  – довжина хвилі світла.

Мірою роздільної здатності дифракційної решітки (спектрального приладу) прийнято вважати відношення довжини хвилі , біля якої виконується вимірювання, до мінімального розділеного інтервалу , тобто Користуючись критерієм Релея, можна показати, що

(6.40)

де m – порядок спектру, N – кількість щілин дифракційної решітки.