22. Дія магнітного поля на струм; сила Ампера. Магнітна взаємодія струмів

Я

Рис. 4.12

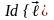к відмічалося вище, магнітне поле діє на вміщений у нього провідник зі струмом. Французький фізик Ампер встановив, що на елемент провідника зі струмом , вміщений в магнітне поле індукцією 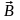, діє сила (сила Ампера)

(4.22)

або в скалярній формі

, (4.23)

де α – кут між напрямками струму та магнітної індукції. Напрямок сили Ампера можна визначити за правилом лівої руки (рис. 4.12).

Сила, що діє на провідник зі струмом скінченої довжини, знаходиться з (4.22) або (4.23) інтегруванням по всій довжині провідника:

(4.24)

Зокрема, для прямолінійного провідника довжиною в однорідному магнітному полі

. (4.25)

Розглянемо тепер взаємодію двох довгих прямолінійних провідників, паралельних один одному і по яких протікають струми однакового напрямку. Ділянки таких провідників зображені на рис. 4.13.

Сила, з якою магнітне поле першого струму діє на ділянку другого провідника довжиною , згідно з (4.25)

.

Згідно з (4.13)

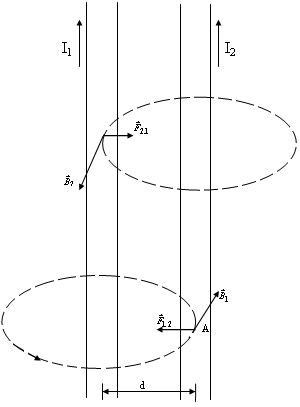
Рис. 4.13

(d – відстань між провідниками).

Як видно з рис. 4.13, кут α між напрямком струму в другому провіднику і вектором магнітної індукції поля першого провідника – прямий; отже, .

Тоді одержимо

. (4.26)

Це і є вираз для сили взаємодії провідників зі струмом (адже так само можна отримати і вираз для сили ). Напрямки сил знайдені за правилом лівої руки і вказані на рис. 4.13. Отже, струми однакового напрямку притягуються. Аналогічно, можна показати, що антипаралельні струми будуть відштовхуватись.

Із формули (4.26), вважаючи в ній всі величини одиничними (за винятком ), отримаємо визначення одиниці сили струму: ампер – це сила такого постійного струму, який при проходженні по двох прямолінійних паралельних нескінченно довгих провідниках, розміщених на відстані 1м у вакуумі, викликає між ними магнітну взаємодію силою на кожен метр довжини. Це визначення використовувалось в СІ до 90-их років минулого століття.

Сила Лоренца. Рух електричних зарядів у магнітному полі

Досліди показують, що на електричний заряд, який рухається в магнітному полі, діє з боку поля сила (сила Лоренца), що напрямлена перпендикулярно до швидкості і пропорційна величині заряду і векторному добутку його швидкості та магнітної індукції:

(4.27)

де α – кут між і .

Д

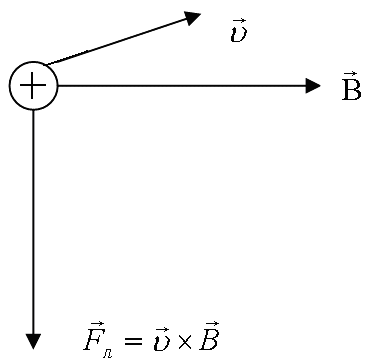Рис. 4.14

ля додатнього заряду напрямок сили Лоренца визначається за правилом лівої руки (рис.4.14), а для від’ємного заряду цей напрямок протилежний (рис.4.15).

Окремо відмітимо, що на нерухомий заряд магнітне поле не діє; в цьому його принципова відмінність від електростатичного поля. Якщо ж на заряд q діють одночасно і електричне, і магнітне поле, то результуюча сила (що також називається силою Лоренца)

, (4.29)

де – напруженість електростатичного поля. Очевидно, що (4.27) є окремим випадком (4.29) у разі, коли електростатичне поле відсутнє.

Я

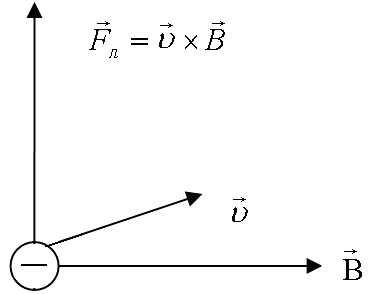Рис. 4.15

кщо заряджена частинка рухається вздовж ліній магнітної індукції (або у протилежному напрямку), то або 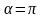. Згідно з (4.28) у цьому випадку 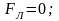магнітне поле на частинку не діє, і вона рухається рівномірно і прямолінійно. Якщо ж швидкість частинки , то 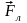– максимальна. Оскільки перпендикулярна до швидкості, то вона надає частинці нормального прискорення; отже, частинка буде рухатися по колу в площині, перпендикулярній до напрямку магнітного поля. Згідно з 2-м законом Ньютона

Я

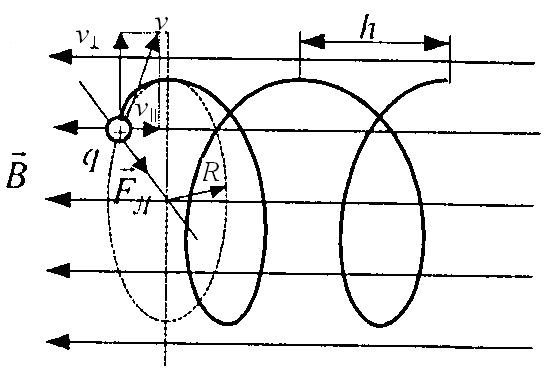Рис. 4.16

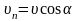кщо ж швидкість частинки складає довільний кут α з напрямком магнітної індукції , то її рух можна розглядати (рис. 4.16) як суперпозицію рівномірного прямолінійного руху вздовж поля зі швидкістю і рівномірного руху по колу радіуса 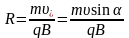в площині, перпендикулярній до поля. Результатом суперпозиції буде рух по спіралі (рис. 4.16). Крок спіралі

. (4.32)

Напрямок, в якому закручується спіраль, залежить від знаку заряду частинки.

З попереднього розгляду видно, що сила Лоренца при русі заряду в магнітному полі роботи не виконує; вона перпендикулярна до швидкості, отже змінює лише напрямок швидкості, не змінюючи її модуля.

23.Магнітний потік — потік вектора магнітної індукції.

Магнітний потік позначається зазвичай грецькою літерою Φ, вимірюється у системі СІ у веберах, у системі СГСМ одиницею вимірювання магнітного потоку є максвел: магнітний потік поля величиною 1 гаус через сантиметр квадратний площі.

Магнітний потік через нескінченно маленьку площадку dS визначається як

,

де B — значення індукції магнітного поля, θ — кут між напрямком поля й нормаллю до поверхні. У векторній формі

.

Магнітний потік псевдоскалярна величина.

Зазвичай магнітний потік обраховується через поверхню, обмежену певним контуром, наприклад, контуром, який утворюють провідники зі струмом. Оскільки в різних точках поверхні магнітна індукція різна, то проводиться інтегрування

Третє рівняння Максвелла

Магнітний потік не залежить від вибору поверхні, яку обмежує контур, а тому потік через замкнену поверхню дорівнює нулю.

.

Це твердження є інтегральною формою третього рівняння Максвелла

Електрорушійна сила

Закон електромагнітної індукції свідчить про те, що при зміні магнітного потоку через контур, обмежений електричним колом, у колі виникає е.р.с.

.

Електромагні́тна інду́кція — виникнення електрорушійної сили у провіднику, що перебуває у змінному магнітному полі.

Явище електромагнітної індукції відкрив у 1831 році Майкл Фарадей. До того було відомо, що електричний струм у провіднику створює магнітне поле. Однак оберненого явища не спостерігалося. Постійне магнітне поле не створює електричного струму. Фарадей встановив, що струм виникає при зміні магнітного поля. Якщо підносити й віддаляти до рамки з провідного матеріалу постійний магніт, то стрілка підключеного до рамки вольтметра відхилятиметься, детектуючи електричний струм. Ще краще це явище проявляється, якщо вставляти (виймати) магнітне осердя в котушку з намотаним провідником.

Фарадей встановив кількісний закон електромагнітної індукції, описавши його рівнянням:

де

 — електрорушійна сила (ЕРС), яка виникає в котушці, що перебуває у змінному магнтіному полі, у вольтах

N — кількість витків у котушці

Φ — магнітний потік у веберах

Якщо в провіднику виникає електрорушійна сила, то відповідно, індукований в ньому струм буде визначатися за законом Ома формулою

,

де R — опір провідника. Такий струм називається індукційним струмом.

Явище електромагнітної індукції використовується у генераторах електричного струму трансформаторах, динамо-машинах, лічильниках електроенергії тощо, тобто є основою виробництва й споживання електричної енергії.

Магні́тне по́ле — складова електромагнітного поля, за допомогою якої здійснюється взаємодія між рухомими електрично зарядженими частинками.

Магнітне поле - складова електромагнітного поля, яка створюється змінним у часі електричним полем, рухомими електричними зарядами або спінами заряджених частинок. Магнітне поле спричиняє силову дію на рухомі електричні заряди. Нерухомі електричні заряди з магнітним полем не взаємодіють, але елементарні частинки з ненульовим спіном, які мають власний магнітний момент, є джерелом магнітного поля і магнітне поле спричиняє на них силову дію, навіть якщо вони перебувають у стані спокою.

Магнітне поле утворюється, наприклад, у просторі довкола провідника, по якому тече струм або довкола постійного магніту.

Магнітне поле є векторним полем, тобто з кожною точкою простору пов'язаний вектор магнітної індукції який характеризує величину і напрям магнітого поля у цій точці і може мінятися з плином часу. Поряд з вектором магнітної індукції , магнітне поле також описується вектором напруженості .

У вакуумі ці вектори пропорційні між собою: , де k - константа, що залежить від вибору системи одиниць. В системі СІ, - так званій магнітній проникності вакууму. Деякі системи одиниць, наприклад СГСГ, побудовані так, щоб вектори індукції та напруженості магнітного поля тотожно дорівнювали один одному: .

Однак у середовищі ці вектори є різними: вектор напруженості описує лише магнітне поле створене рухомими зарядами (струмами) ігноруючи поле створене середовищем, тоді як вектор індукції враховує ще й вплив середовища:

^[1]

де - вектор намагніченості середовища.

Утворення магнітного поля

На відміну від електричних зарядів, магнітних зарядів, що створювали б магнітне поле аналогічним чином, не спостерігається. Теоретично такі заряди, які отримали назву магнітних монополів, могли б існувати. В такому випадку електричне і магнітне поле були б повністю симетричними.

Таким чином, найменшою одиницею, яка може створювати магнітне поле, є магнітний диполь. Магнітний диполь відрізняється тим, що в нього завжди є два полюси, в яких починаються і кінчаються силові лінії поля. Мікроскопічні магнітні диполі зв'язані зі спінами елементарних частинок. Магнітний диполь мають як заряджені елементарні частинки, наприклад, електрони, так і нейтральні, наприклад, нейтрони. Елементарні частинки з відмінним від нуля спіном можна уявити собі як маленькі магнітики. Зазвичай, частинки з протилежними значеннями спінів спарюються, що призводить до компенсації створених ними магнітних полів, але в окремих випадках можливе вирівнювання спінів багатьох частинок в одному напрямку, що призводить до утворення постійних магнітів.

Магнітне поле - також створюється рухомими електричними зарядами, тобто електричним струмом.

Створенне електричним зарядом поле залежить від системи відліку. Відносно спостерігача, що рухається з однаковою із зарядом швидкістю, заряд нерухомий, і такий спостерігач фіксуватиме тільке створене ним електричне поле. Інший спостерігач, що рухається з іншою швидкістю, фіксуватиме як електричне, так і магнітне поле. Таким чином, електричне і магнітне поля взаємозв'язані, і є складовими частинами загального електромагнітного поля.

При протіканні електричного струму через провідник він залишається електрично нейтральним, однак носії заряду в ньому рухаються, тому навколо провідника виникає тільки магнітне поле. Величина цього поля визначається законом Біо-Савара, а напрям можна визначити за допомогою правила Ампера або правила правої руки. Таке поле є вихровим, тобто його силові лінії замкнуті.

Магнітне поле створюється також змінним електричним полем. За законом електромагнітної індукції змінне магнітне поле породжує змінне електричне поле, що також є вихровим. Взаємне створення електричного і магнітного поля змінними магнітним і електричним полем призводить до можливості розповсюдження в просторі електромагнітних хвиль.

Дія магнітного поля

Дія магнітного поля на рухомі заряди визначається силою Лоренца.

Сила, що діє на провідник зі струмом у магнітному полі називається силою Ампера. Сили взаємодії провідників зі струмом визначаються законом Ампера.

Нейтральні речовини без електричного струму можуть втягуватися в магнітне поле (парамагнетики) або виштовхуватися з нього (діамагнетики). Виштовхування діамагнетиків з магнітного поля можна використати для левітації.

Феромагнетики намагнічуються в магнітому полі й зберігають магнітний момент при знятті прикладеного поля.

Енергія магнітного поля

Енергія магнітного поля в просторі задається формулою

.

Відповідно, густина енергії магнітного поля дорівнює

.

Енергія магнітного поля провідника зі струмом дорівнює:

,

де - сила струму, а - індуктивність, що залежить від форми провідника.