20. Закон Ома для неоднорідної ділянки кола і для повного кола

Р

Рис.3.28

озглянемо два провідники заряджені електричними зарядами до потенціалів і . З’єднаємо ці провідники третім провідником по якому потече електричний струм силою І (рис. 3.28). Будемо підтримувати силу струму постійною. Для цього з допомогою спеціального пристрою силами неелектричної природи будемо переносити електричні заряди в зворотному напрямку таким чином, щоб різниця потенціалів між тілами залишалась постійною. Сили неелектричної природи, які переносять заряди в даному пристрої, називаються сторонніми. Пристрій, в якому сторонні сили переносять електричні заряди між двома тілами і підтримують постійною різницю потенціалів між ними називається джерелом струму, а тіла, між якими підтримується постійною різниця потенціалів, називаються полюсами джерела струму. Замкнутий контур , утворений джерелом струму і провідником, під’єднаним до його полюсів, утворюють електричне коло.

Знайдемо роботу, яку необхідно виконати, щоб перемістити деякий заряд по замкнутому контуру

. (3.180)

Ця робота складається з роботи електричних сил і роботи сторонніх сил. Оскільки електростатичні сили потенціальні, то робота цих сил по замкнутому контурі рівна нулю

. (3.181)

Підставивши (3.181) у вираз (3.180), дістанемо

. (3.182)

Введемо фізичну величину , яка називається електрорушійною силою

. (3.183)

Е

Рис.3.29

лектрорушійною силою називається фізична величина, рівна роботі сторонніх сил по переміщенню одиничного позитивного заряду по замкнутому електричному колу.

Розглянемо неоднорідну ділянку електричного кола, тобто таку ділянку, яка містить джерело електричного струму з електрорушійною силою і внутрішнім опором, тобто опором самого джерела струму . Нехай до ділянки кола прикладена різниця потенціалів ( рис. 3.29 ). Нехай опір провідників ділянки рівний і по провідниках ділянки тече постійний струм силою . Згідно із законом Ома для ділянки кола (3.162), сила струму рівна

, (3.184)

де – повний опір ділянки кола. Згідно з означенням електричної напруги у випадку постійного струму за формулою (3.161), одержимо

. (3.185)

Із формули (3.183) робота сторонніх сил рівна

. (3.186)

Робота електростатичних сил рівна

. (3.187)

Підставимо (3.186) і (3.187) у формулу (3.185)

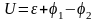. (3.188)

Підставимо (3.188) у вираз (3.184), одержимо

. (3.189)

Ф

Рис.3.30

ормула (3.189) – це закон Ома для неоднорідної ділянки кола: сила струму в неоднорідній ділянці кола прямо пропорційна сумі електрорушійної сили на ділянці, різниці потенціалів на кінцях ділянки і обернено пропорційна повному опору ділянки.

Розглянемо повне замкнене електричне коло, яке можна отримати з неоднорідної ділянки кола, з’єднавши точки 1 і 2 (рис.3.30).

В цьому випадку потенціали цих точок зрівняються і вираз (3.179) набере вигляду

. (3.190)

Отриманий вираз – це закон Ома для повного кола: сила струму в колі прямо пропорційна електрорушійній силі джерела струму і обернено пропорційна повному опору кола.

Розгалужені електричні кола. Закони Кірхгофа. З’єднання провідників

Для розрахунку складних розгалужених електричних кіл зручно користуватись законами Кірхгофа, які є наслідками закону збереження електричного заряду і законів Ома.

Вузлом електричного кола називається місце з’єднання трьох або більше провідників. Розглянемо деякий вузол А (рис.3.31). В стаціонарному випадку заряд і потенціал точки А повинен залишатись постійним. Виходячи із закону збереження електричного заряду можна записати

, (3.191)

д

Рис. 3.31

е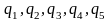 – заряди, які за деякий однаковий проміжок часу надходять до вузла А чи виходять із нього. Продиференціюємо вираз (3.191)

. (3.182)

Враховуючи формулу (3.156) вираз (3.192) можна представити у вигляді

. (3.193)

Будемо вважати сили струмів, які сходяться у вузлі, алгебраїчними величинами. Зокрема, струми, які ідуть до вузла, будемо вважати додатними, а струми, які ідуть від вузла, будемо вважати від’ємними. Тоді в загальному випадку, коли у вузлі сходиться провідників, формулу (3.193) можна представити у вигляді

. (3.194)

Ф

Рис.3.32

ормула (3.194) є математичним записом першого закону Кірхгофа: алгебраїчна сума сил струмів, які сходяться у вузлі, рівна нулю. При цьому струми, які йдуть до вузла вважаються додатніми, а струми, які йдуть від вузла – від’ємними.

Розглянемо довільний замкнутий контур, який умовно виділимо в складному розгалуженому електричному колі (рис. 3.32). Будемо вважати, що внутрішні опори джерел струму рівні нулю. На кожній ділянці контуру виберемо довільним чином напрямки струмів. Виберемо довільним чином напрямок обходу по контуру, який будемо вважати додатнім. Запишемо для кожної ділянки контуру закон Ома для неоднорідної ділянки кола

. (3.195)

Помножимо кожне з рівнянь системи (3.195) на опори 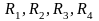відповідно

. (3.196)

Додамо алгебраїчно рівняння системи (3.196)

. (3.197)

Якщо виділений контур містить n ділянок, то формула (3.197) в загальному випадку може бути представлена у вигляді

. (3.198)

Це математичний запис другого закону Кірхгофа: при обході по замкнутому контурі алгебраїчна сума добутків сил струмів на опори рівна алгебраїчній сумі електрорушійних сил. При цьому струм вважається додатнім, якщо його напрямок співпадає з напрямком обходу за контуром; електрорушійна сила вважається додатною, якщо при обході здійснюється перехід через неї із знаку “мінус” на знак “плюс”.

С

Рис.3.33

еред різних видів з’єднання провідників найпростішими і найважливішими є послідовне і паралельне з’єднання.

Розглянемо послідовне з’єднання провідників. При цьому з’єднанні електричне коло не має розгалужень, усі провідники ввімкнені в коло по черзі, один за одним. На рис.3.33 показано з’єднання двох провідників з опорами і . При проходженні постійного струму електричний заряд не нагромаджується в жодному з провідників. За один і той же проміжок часу через поперечний переріз кожного з провідників проходить один і той же заряд, а значить сила струму в усіх провідниках однакова

. (3.199)

При проходженні заряду послідовно через усі провідники виконується робота, яка рівна сумі робіт виконаних на кожному провіднику. Тому загальна напруга рівна сумі напруг на всіх провідниках

. (3.200)

Поділимо вираз (3.200) на силу струму І. Врахувавши при цьому (3.199), одержимо

. (3.201)

Із закону Ома для ділянок кола (3.162) випливає, що

. (3.202)

З врахуванням формули (3.202) вираз (3.201) набере вигляду

. (3.203)

Формула (3.203) дозволяє визначити загальний опір при послідовному з’єднанні двох провідників. Якщо послідовно з’єднано n провідників, то формула (3.203) набере вигляду

. (3.204)

Р

Рис.3.34

озглянемо паралельне з’єднання двох провідників з опорами і (рис. 3.34). При такому з’єднанні початки всіх провідників з’єднуються в одному вузлі, а кінці провідників – в іншому вузлі. Оскільки потенціали початків провідників у вузлі А рівні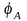 , а потенціали кінців провідників у вузлі В рівні 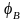, то різниці потенціалів і напруги на всіх провідниках однакові

. (3.205)

У випадку постійного струму в будь-якій точці електричного кола, в тому числі і у вузлі А, заряди не накопичуються. Тому сила струму, який надходить до вузла А повинна дорівнювати сумі сил струмів, які виходять з цього вузла.

. (3.206)

Поділимо вираз (3.206) на напругу і врахувавши (3.195), одержимо

. (3.207)

Із закону Ома для ділянки кола отримаємо

. (3.208)

З врахуванням виразу (3.208) формула (3.207) набере вигляду

. (3.209)

Формула (3.209) дозволяє визначити загальний опір при паралельному з’єднанні двох провідників. Якщо паралельно з’єднано n провідників то формула (3.209) набере вигляду

. (3.210)