§2. Дисперсия и среднее квадратическое отклонение

При описании некоторых явлений среднее арифметическое дает о них примерное представление, вполне удовлетворительное для практических целей. Таково, например, среднее число правонарушений в день, рас­смотренное в примере 1 (§1). Однако весьма часто встре­чаются такие ситуации, для описания которых недоста­точно знать только среднее арифметическое.

История первая. Двух студентов юридического фа­культета послали на практику, одного в город Дрюково, другого — в город Стуково. Практиканты узнали, что в это время года среднесуточная температура в этих горо­дах равна нулю. Тот из них, кто поехал в Стуково, бу­дучи человеком осторожным, взял с собой только теплые вещи. Другой, более легкомысленный, оделся по-летнему. Оказалось, что в течение всей практики в обоих городах температура была стабильной: в Дрюкове — +2 днем и –2 ночью, в Стукове — +15 днем и –15 ночью. В результате, несмотря на то, что среднесуточная темпе­ратура действительно была нулевой, оба студента забо­лели, так как один постоянно перегревался, а другой — постоянно мерз.

История вторая. Один из торговцев в Дрюкове был очень набожным человеком. Как-то раз, под впечатлени­ем воскресной проповеди о пользе благотворительности, он в первой половине недели сдавал каждому покупателю сдачу на 1000 руб. больше, чем нужно. Но потом дей­ствие проповеди ослабело, и нашего торговца одолела природная корысть. В следующие три дня он уже обма­нывал каждого покупателя, беря со всех на 1000 руб. больше. Поскольку число покупателей в первые и после­дние три дня недели было одинаковым, то получается, что в среднем размер неправильной сдачи равен нулю, т.е. в среднем покупатели получали сдачу правильно!

Из этих историй видно, что, помимо средней вели­чины, нужно знать еще и то, как заданные числа рассе­яны около их среднего значения. Для этой цели вводят­ся дисперсия и среднее квадратическое отклонение.

Дисперсией величин х₁, х₂, ... , х_n называется число

Пример 1. На обследование каждого из десяти авто­мобилей было затрачено следующее время (в мин):

Таблица 3

Здесь символом х_i обозначено время, затраченное на обследование автомобиля с номером i. Найти дисперсию величин x_i.

Решение. Составим таблицу из трех столбцов:

Таблица 4

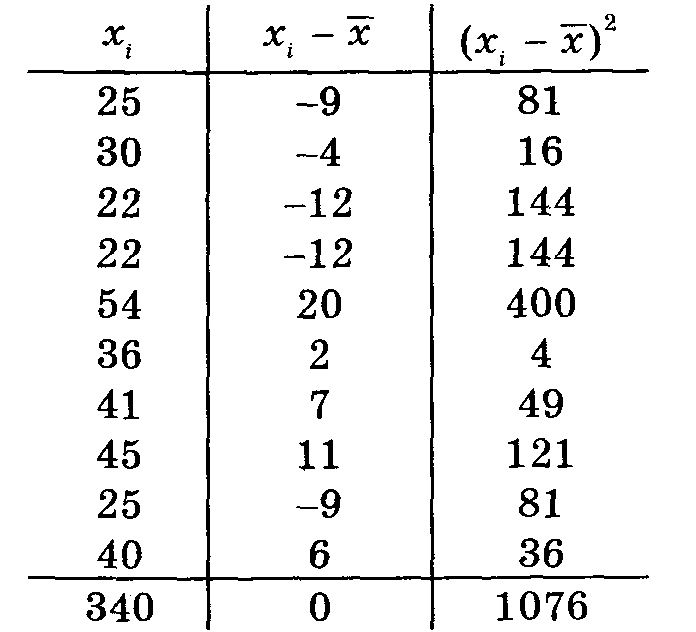
В последней строке первого столбца записано общее время обследования всех автомобилей, т.е. сумма всех чисел x_i — 340. Поделив ее на 10, найдем среднее арифметическое чисел х₁, х₂, ...,x₁₀: = 34 (мин).

Во втором столбце записаны разности , , ... , , представляющие собой отклонения величин х₁, х₂, ...,x₁₀ от их среднего. Сумма отклонений всег­да равна нулю, что показано в последней строке второго столбца. Это важнейшее свойство средней величины.

В третьем столбце табл. 4 записаны квадраты отклонений: ( )², ( )², ... , ( )².

Сумма квадратов, как видно из последней строки, равна 1076. По формуле (5) находим дисперсию D:

Если известны частоты , то для вычисления дисперсии вместо формулы (5) можно использовать формулу

где, как и выше, суть различные среди заданных чисел .

Средним квадратическим отклонением величин от их среднего значения называется величина

(7)

В примере 1 среднее квадратическое отклонение равно

(мин).

Из формулы (5) видно, что дисперсия представляет собой среднее арифметическое квадратов разностей , , ... , . Поэтому величину S можно рассмат­ривать как среднее отклонение величин от их среднего значения .

Из определения дисперсии и среднего квадратического отклонения следует, что последнее не превышает наибольшей из величин (абсолютная величина отклонения). Так, в первом примере 10,4 < 20, т.е. S существенно меньше максимального отклонения. Зато в историях, которые мы рассказали в начале параграфа, среднее квадратическое отклонение S является макси­мально возможным, так как все отклонения от среднего значения одинаковы по абсолютной величине. Вычислив по формулам (5) и (6) среднее квадратическое отклоне­ние температуры в Дрюкове и Стукове, мы найдем, что оно равно максимальной температуре (2 и 15 соответ­ственно); во второй истории среднее квадратическое от­клонение будет 1000 руб., что также совпадает с вели­чиной максимального отклонения.

Прежде чем двигаться дальше, необходимо ввести весьма важное понятие переменной величины. В приме­ре 1 центральную роль играет табл. 3, в которой каж­дому автомобилю ставится в соответствие время его об­следования. Математики в этом случае говорят, что время обследования есть переменная величина X, при­нимающая значения . В примере 2 из §1 переменной величиной является число правонарушений, в примере 3 — прибыль страховой компании.

Теперь допустим, что нужно обследовать все автомо­били города Дрюкова. Но число автомобилей так вели­ко, что описать все значения величины Х (X — время обследования) практически невозможно. Однако мы можем, не проводя самого обследования, предсказать его результаты приближенно, с помощью примера 1. Предварительно, используя табл. 3, составим другую таблицу, в которой укажем время обследования и со­ответствующую частоту :

Таблица 5

Обычно, прогноз содержит следующую информацию о величине X:

1) диапазон значений величины X,

2) среднее значение ,

3) среднее квадратическое отклонение S,

4) интервал наиболее вероятных значений величины X,

5) долю значений величины X, попадающих в заданный промежуток.

По данным примера 1:

время обследования автомобиля изменяется в пределах от (22 – х) до (54 – х) мин,

среднее время обследования одного автомобиля — = 34 мин,

среднее отклонение величины Х от ее среднего значения составляет S = 10,4 мин.

Интервалом наиболее вероятных значений величины Х обычно называют интервал, серединой которого явля­ется точка — среднее арифметическое, и в который попадает более половины значений величины X. Рас­смотрим, например, интервал ( – S; + S). Имеем: – S = 23,6 и + S = 44,4. Из табл. 5 видно, что в ин­тервале 23,6 – 44,4 содержится 5 значений величины X: 25, 30, 36, 40, 41. Их частоты соответственно равны 0,2; 0,1; 0,1; 0,1; 0,1. Суммарная частота будет 0,6. Это чис­ло составляет 60% от единицы, т.е. от суммы всех час­тот. Следовательно, в интервал 23,6 – 44,4 попадает 60% (т.е. большая часть) значений величины X. Таким обра­зом, этот интервал является интервалом наиболее веро­ятных значений величины X. Доля значений величины X, попавших в какой-либо другой интервал, оценивает­ся так же. Обычно оценивают долю больших и малых значений. В нашем примере доля автомобилей, на об­служивание которых затрачивается меньше 23,6 мин, составляет 20% от общего количества автомобилей (в табл. 5 имеется одно такое значение — 22, и его час­тота равна 0,2). Доля автомобилей, на обслуживание которых затрачивается больше 44,4 мин, составляет также 20% от общего количества автомобилей.

При обработке статистического материала используется специальная терминология. Совокупность всех рас­сматриваемых объектов называют генеральной совокуп­ностью, а часть объектов, каким-либо способом выб­ранных для обследования, называют выборкой. В нашем примере с автомобилями генеральную совокупность об­разуют все автомобили города Дрюкова, а выборку — те 10 автомобилей, которые рассматривались в примере 1.

Очень важно сделать выборку правильно. От этого зависит, насколько точными и достоверными будут по­лученные выводы, результаты прогноза. В математичес­кой статистике изучаются способы отбора, позволяющие сделать выборку так, чтобы полученная с ее помощью информация давала достаточно полное и адекватное представление об интересующем нас признаке изучае­мой генеральной совокупности. Тогда найденные с по­мощью выборки среднее арифметическое и D диспер­сия будут близки к гипотетическим величинам — сред­нему арифметическому и дисперсии, которые могли бы быть получены при обработке всей генеральной сово­купности.