И сследование планетарных и дифференциальных передач

Существует два метода исследования планетарных и дифференциальных передач:

аналитический – метод Виллиса,

графический – метод диаграмм Смирнова – Кутцбаха.

Аналитический метод исследования планетарных и дифференциальных передач

Аналитический метод основан на принципе обращения движения звеньев и состоит в том, что исследуется относительное движение звеньев механизма, которое они совершают по отношению к водилу.

Поскольку планетарные и дифференциальные механизмы содержат звенья с подвижными геометрическими осями вращения, то воспользоваться формулой для определения передаточных отношений между звеньями механизма через числа зубьев не представляется возможным. Метод обращения движения – искусственный приём, позволяющий рассматривать планетарный или дифференциальный механизм, как механизм с неподвижными геометрическими осями вращения.

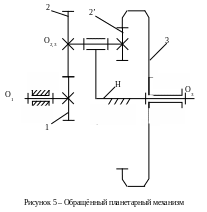
Всем звеньям механизма сообщаем дополнительную угловую скорость, равную по модулю угловой скорости водила _н, но противоположную по направлению. Тогда все звенья будут иметь иную угловую скорость, отличающуюся от действительной на - _н. Водило Н будет неподвижно. Но при этом все звенья будут совершать только вращательное движение. Этот прием равносилен тому, что мы водило превращаем в стойку (рисунок 5). Если часы с центральной секундной стрелкой вращать против хода секундной стрелки, так чтобы она была неподвижной, тогда угловые скорости: секундной стрелки _с-_с=0, минутной стрелки _м-_с, часовой стрелки _ч-_с, корпуса часов 0-_с=-_с.

В планетарном механизме (рисунок 3б) закрепляем водило Н и раскрепляем солнечное колесо 3. В обращённом редукторе (рисунок 5) все звенья совершают вращательное движение. Анализ обращённого планетарного механизма ничем не будет отличаться от анализа простого ступенчатого редуктора. Составим таблицу угловых скоростей звеньев в планетарном и обращённом механизмах (таблица 1).

Таблица 1

Звенья	Планетарный механизм		Обращённый механизм
	вид движения	угловая скорость	вид движения	угловая скорость
1	вращение	1	вращение	1-н
2-2’	плоскопар.	2-2’	вращение	2-2’-н
3	неподвижно	0	вращение	-н
Н	вращение	н	неподвижно	0

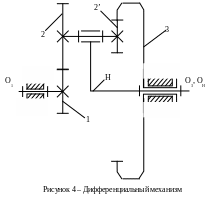
Определим передаточное отношение в обращённом механизме от звена 1 к звену 3:

.

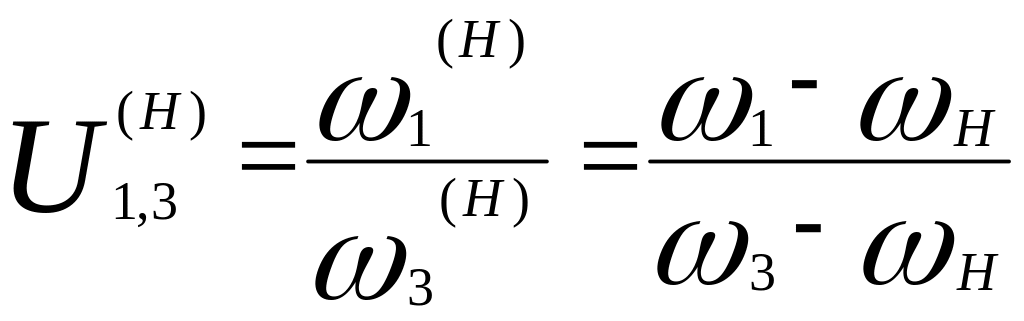Полученная формула впервые была получена Виллисом для планетарных и дифференциальных механизмов. Поскольку в реальном планетарном редукторе ₃=0, то получим следующие выражение:

.

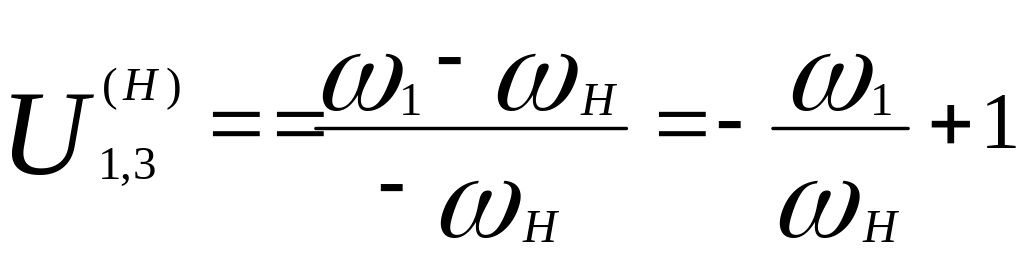Здесь - передаточное отношение от звена 1 к водилу .

Следовательно:

.

Это частный случай формулы Виллиса для определения передаточного отношения планетарного механизма.

Если заданы числа зубьев всех колёс в планетарных редукторах (рисунок 3а, 3б, 3в), то передаточное отношение в обращённых механизмах легко определить:

а) ;

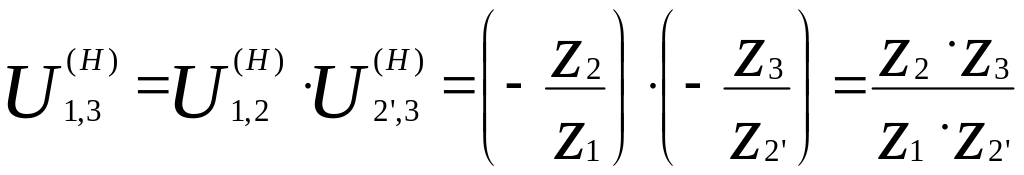б) ;

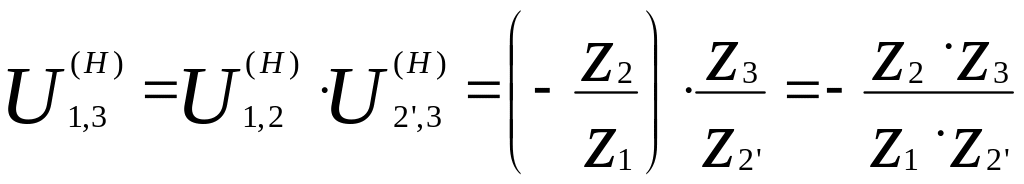в) .

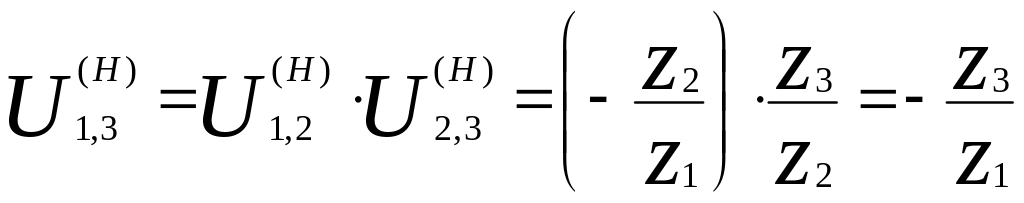При подстановке полученных значений в формулу, для определения передаточных отношений в планетарном редукторе получим:

а) ;

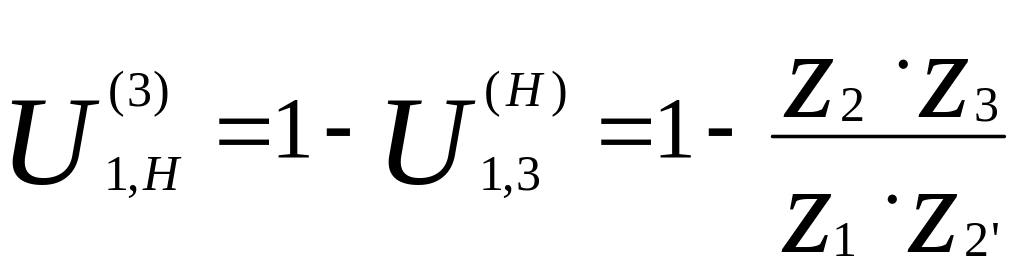б) ;

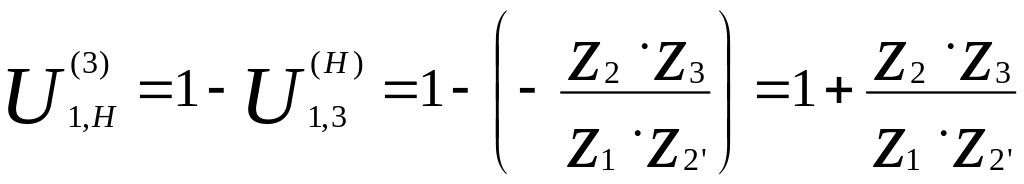в) .

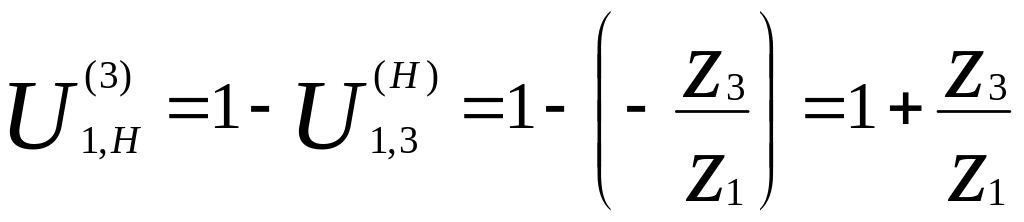Проанализируем дифференциальный редуктор, изображённый на рисунке 4. Рассмотрим движение звеньев в дифференциальном и обращённом механизмах. Составим таблицу угловых скоростей звеньев (таблица 2).

Таблица 2

Звенья	Дифференциальный механизм		Обращённый механизм
	вид движения	угловая скорость	вид движения	угловая скорость
1	вращение	1	вращение	1-н
2-2’	плоскопар.	2-2’	вращение	2-2’-н
3	вращение	3	вращение	3-н
Н	вращение	н	неподвижно	0

В дифференциальном механизме колесо 3 не закреплено и имеет свою угловую скорость ₃  0. Если водило Н в обращённом дифференциальном механизме неподвижно, то дифференциальный редуктор превращается в простой, и анализ его тогда ничем не отличается от анализа простых редукторов. При этом необходимо учитывать, что угловые скорости звеньев в обращенном механизме отличаются от угловых скоростей в реальном механизме на - _н.

Предположим, что нам заданы числа зубьев всех колёс z₁, z₂, z_2’, z₃ и угловые скорости ₁ и ₃. Необходимо определить угловую скорость водила _н.

Определяем передаточное отношение от звена 1 к звену 3 в обращённом механизме:

.

Определяем это передаточное отношение через числа зубьев:

;

Подставляем полученное значение в предыдущее выражение:

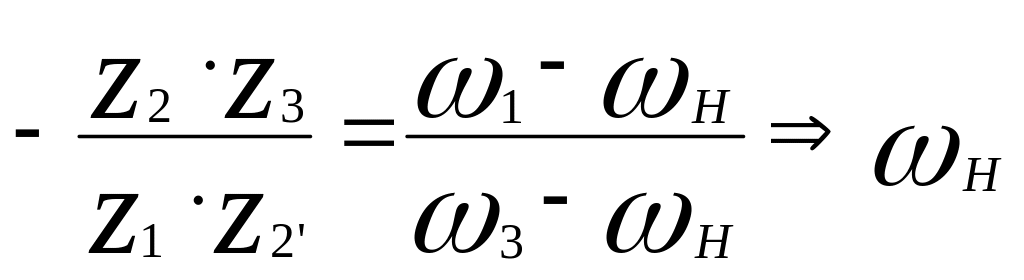
и определяем _н.

Если нам необходимо определить передаточное отношение от любого звена к любому в планетарном или дифференциальном механизмах, то необходимо рассматривать такие механизмы в обращённом движении (с закреплённым водилом) и определять передаточное отношение между звеньями в обращённом движении. Передаточное отношение, выраженное в угловых скоростях, в обращённом механизме в общем виде от звена « » к звену « » будет иметь следующий вид:

.

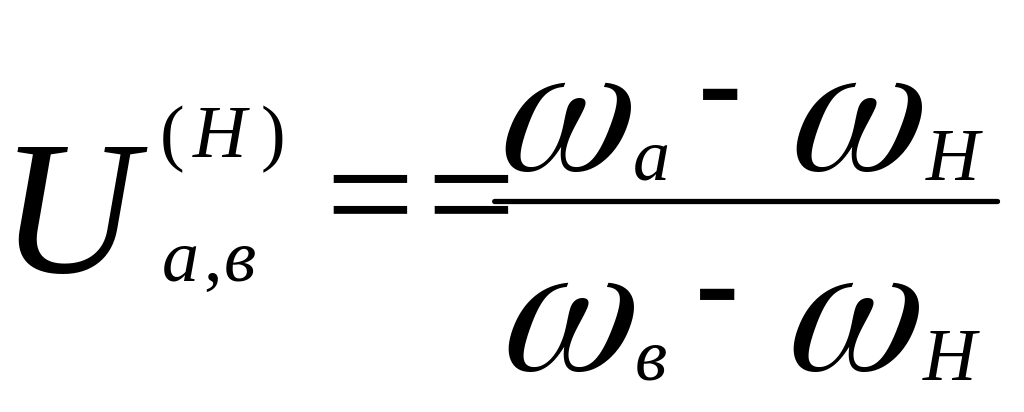Если звено « » неподвижно ( =0), то формула приобретает вид:

.

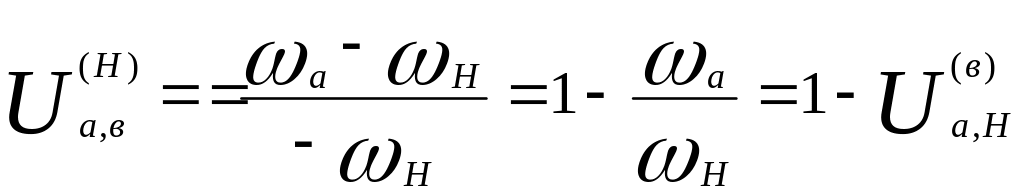Пользуясь методом Виллиса можно определить угловые скорости любых звеньев планетарных и дифференциальных механизмов а также передаточное отношение между любыми звеньями этих механизмов.