8

Механизмы передачи вращательного движения

Лекция 2

Теорема об общем передаточном отношении при последовательном соеди­нении

механизмов передачи вращательного движения

М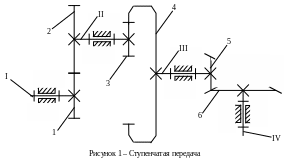 ы рассмотрели простые механизмы передачи вращательного движе­ния – трёхзвенные. Применение таких механизмов ограничено в связи с малым передаточным отношением. Для получения больших передаточных отношений на практике используют последовательное соединение нескольких простых ме­ханизмов – передач. Такие механизмы (редукторы) называют многоступенча­тыми. Последовательно соединённые передачи называют ступенями.

Определим общее передаточное отношение механизма, изображён­ного на рисунке 1. Обозначим валы римскими цифрами а зубчатые колёса – арабскими. Механизм содержит три простые ступени, 4 вала и 6 зубчатых колёс. 1-2 – зубчатая цилиндрическая передача внешнего зацепления, 3-4 – зубчатая цилиндрическая передача внутреннего зацепления, 5-6 – коническая зубчатая передача.

Общее передаточное отношение механизма равно отношению угловых скоростей входного (I) и выходного (IV) звеньев:

.

Определим передаточное отношение каждой ступени:

; ; .

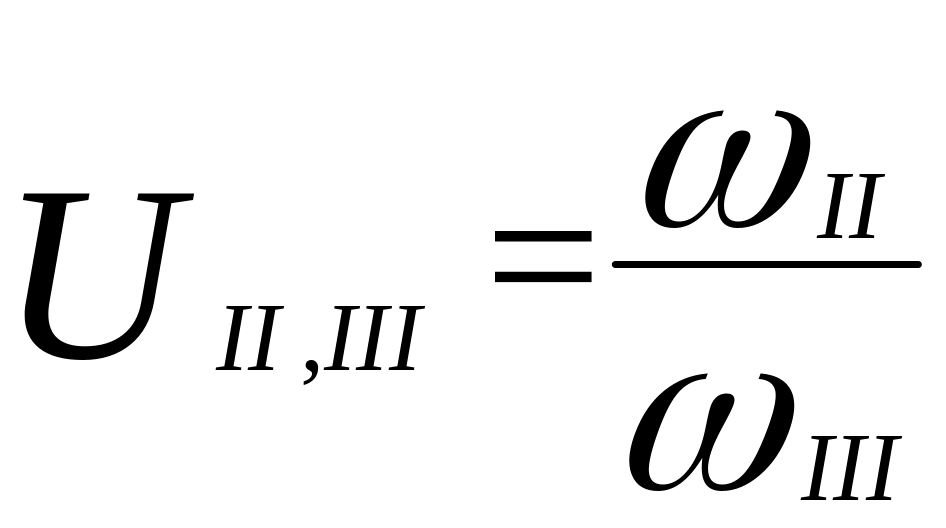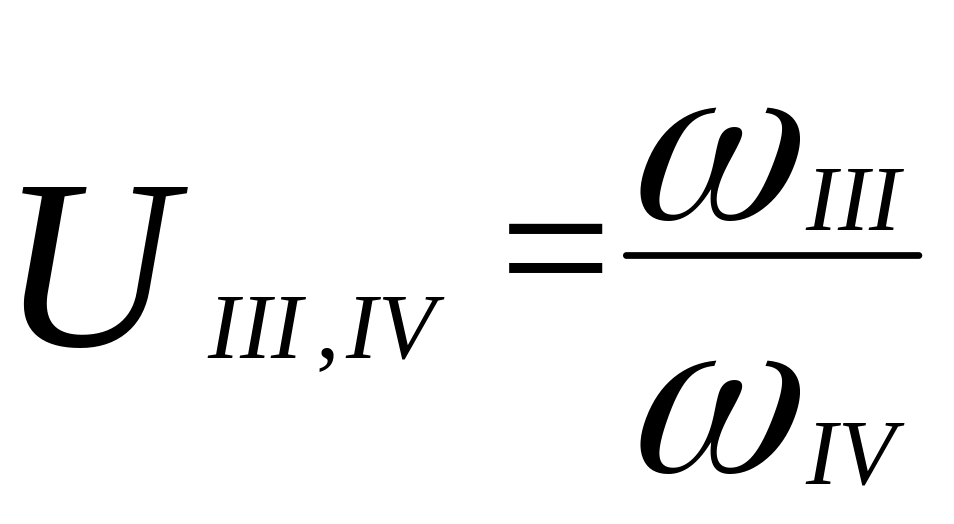Перемножим левые и правые части полученных равенств:

.

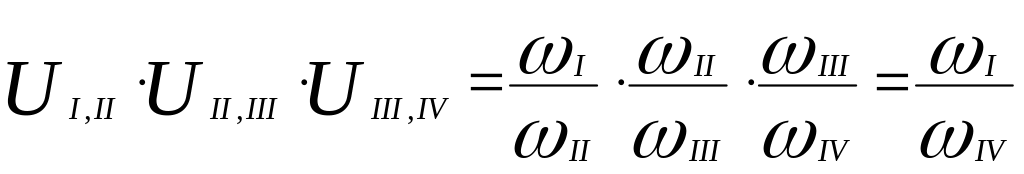Следовательно:

.

Общее передаточное отношение при последовательном соединении механизмов передачи вращательного движения равно произведению передаточных отношений всех последовательно соединённых передач.

При этом необходимо учитывать, что если оси вращения входного и выходного звеньев не параллельны, то передаточное отношение определяется только по модулю.

Определим общее передаточное отношение механизма через количество зубьев каждой пары зубчатых колёс:

; ; ; .

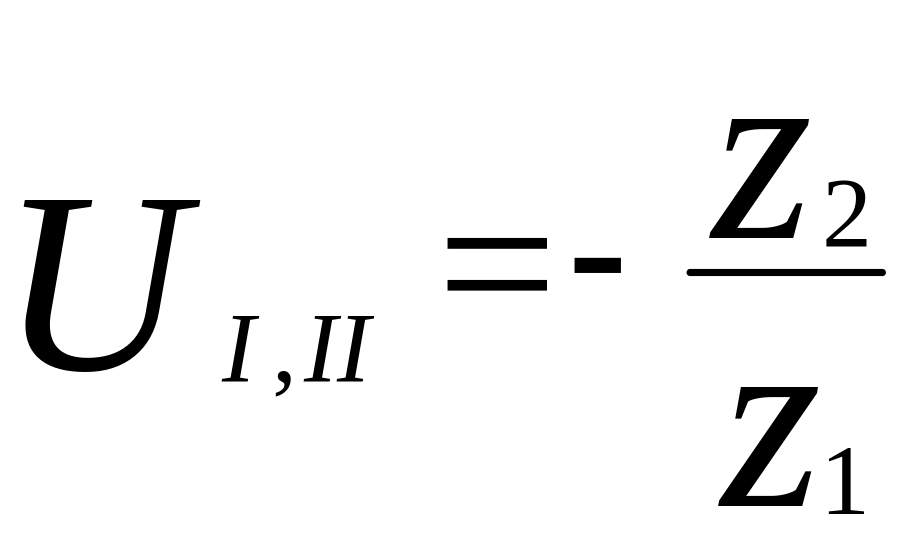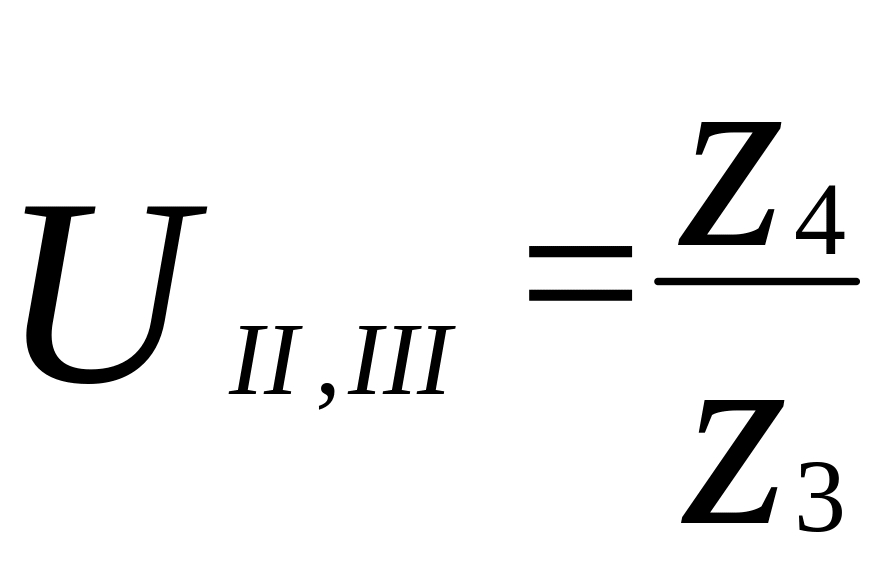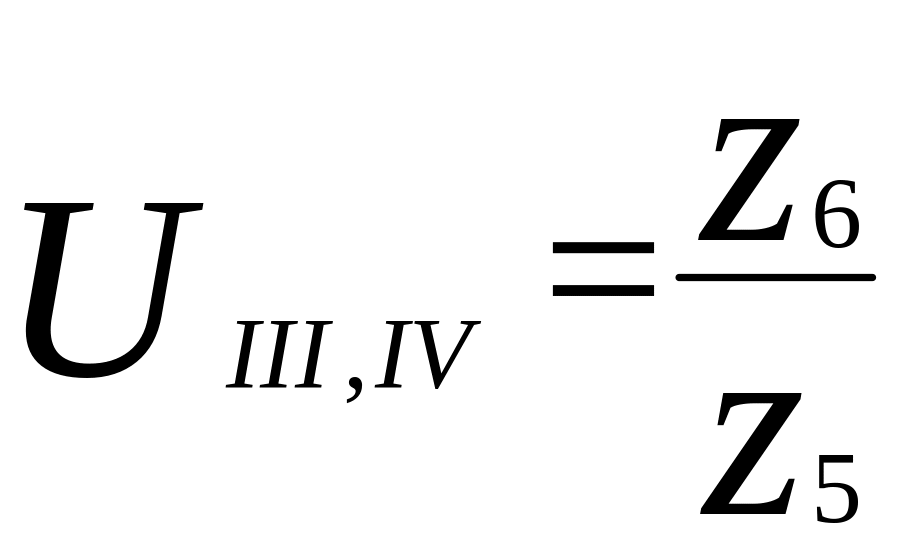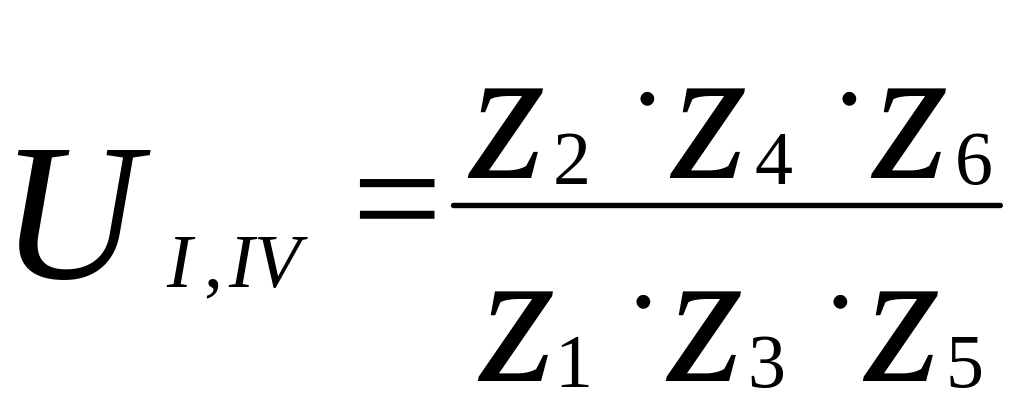Зубчатый механизм, у которого вращение передаётся от ступени к ступени (редуктор) называется ступенчатым.

Рассмотрим другой вид редуктора – однорядный редуктор (рисунок 2). Числа зубьев колёс заданы: z₁, z₂, z₃,z₄, z₅. Передачи соединены последовательно и расположены в один ряд.

Определим общее передаточное отношение однорядного редуктора:

.

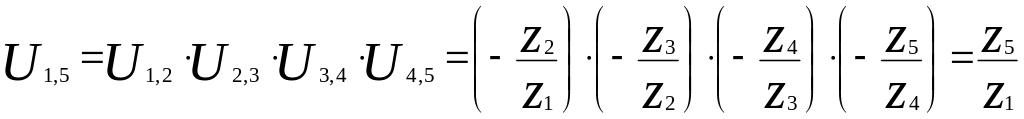И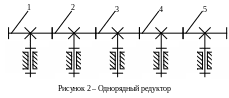 з полученного результата видно, что общее передаточное отношение в рядном редукторе не зависит от чисел зубьев промежуточных колёс. Колёса, не оказывающие влияния на модуль передаточного отношения, называют паразитными. В передачах они применяются с целью увеличения межосевого расстояния входного и выходного звеньев и для изменения направления вращения выходного (ведомого) вала.

Рассмотренные нами механизмы, это механизмы у которых все звенья совершают вращательное движение (за исключением неподвижной стойки). В технике часто встречаются механизмы передачи вращательного движения, которые содержат звенья, совершающие сложное движение, например плоскопараллельное.

Планетарные и дифференциальные передачи

Различают зубчатые механизмы передачи вращательного движения простые и эпициклические.

Простыми называются зубчатые механизмы, у которых геометрические оси вращения всех колёс в процессе нормальной работы механизма друг относительно друга остаются неподвижными.

К эпициклическим относятся механизмы, у которых некоторые звенья совершают сложное движение и точки звеньев описывают траектории – эпи и гипоциклоиды. К этим механизмам относятся планетарные и дифференциальные механизмы.

Планетарными и дифференциальными называются передачи, у которых геометрические оси вращения некоторых звеньев перемещаются в пространстве, т. е. зубчатые колёса совершают сложное движение, в частном случае – плоскопараллельное.

Рассмотрим планетарные механизмы, изображенные на рисунке 3. Это эпициклические механизмы, имеющие степень подвижности равную 1. Если эпициклический механизм имеет степень подвижности больше 1, он называется дифференциальным.

На рисунке 3 изображены основные типы планетарных механизмов. Во всех трёх схемах (а, б, в) содержатся одинаковые звенья. Зубчатые колёса, оси которых неподвижны, называются центральными (звенья 1,3). Зубчатые колёса, которые полностью неподвижны (закреплены), называются солнечными (звенья 3). Зубчатые колёса с подвижными геометрическими осями вращения называются сателлитами (звенья 2- 2’). Звено, переносящее ось сателлита, называется водилом (звено Н).

Работа механизма заключается в следующем: колесо 1, вращаясь вокруг оси О₁, приводит в движение колесо 2, которое жестко связано с колесом 2’. Колесо 2’, обкатываясь по неподвижному колесу 3, увлекает водило Н во вращательное движение.

Определим степень подвижности механизмов по формуле Чебышева. Количество звеньев n=4. Количество кинематических пар 2^го класса Р₂=3 (одноподвижные шарнирные соединения). Количество кинематических пар 1^го класса Р₁=2 (двухподвижные кинематические пары – зубчатое зацепление).

W=3(n-1)-2Р₂-Р₁=3(4-1)-23-2=1.

Любой из изображенных планетарных механизмов можно преобразовать в дифференциальный, освободив солнечное колесо 3. Для этого необходимо свободный конец рукояти (водила) Н связать через подвижное соединение со станиной и установить солнечное колесо на станине через подвижное соединение (рисунок 4). Определим степень подвижности полученного механизма:

n=5, P₂=4, P₁=2,

W=3(n-1)-2Р₂-Р₁=3(5-1)-24-2=2.

В планетарном механизме достаточно задать одну обобщённую координату (например закон движения звена 1), чтобы определить положения всех остальных звеньев. В дифференциальном механизме, изображенном на рисунке 4, необходимо задаться двумя обобщёнными координатами (например звена 1 и звена 3), чтобы можно было определить положения всех остальных звеньев.