Многократное рассеяние.

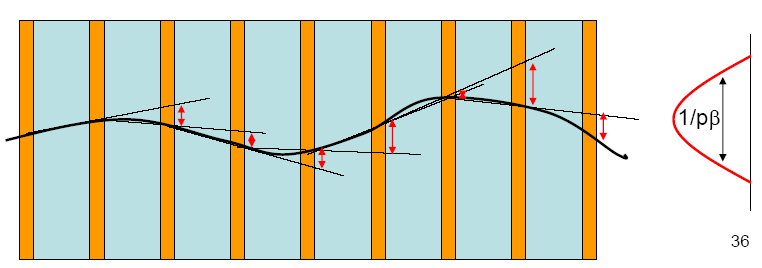
Проходя через достаточно толстый слой вещества, частица претерпевает много столкновений с ядрами. Этот процесс упругих кулоновских столкновений носит название многократного рассеяния. В каждом элементарном акте такого процесса частица рассеивается преимущественно на малый угол. В результате многократного рассеяния параллельный пучок частиц приобретает некоторый угловой разброс, сохраняя азимутальную симметрию.

При прохождении через вещество частицы претерпевают многократное рассеяние. Если заряженная частица движется в плотной среде, то, проходя мимо различных ядер этой среды в пределах b < bmax, она будет рассеиваться каждым из них на некоторый угол θ, среднее значение которого тем больше, чем меньше масса движущейся частицы и чем меньше ее энергия. Этот процесс упругих рассеяний

частицы в кулоновском поле ядер, мимо которых она движется, называется многократным кулоновским рассеянием.

Пусть в результате N столкновений на пути x частица испытает

последовательную серию отклонений θ1,θ2,…θN. Каждый из этих углов

определяется конкретными условиями данного столкновения

(например, значением параметра удара bi), так что вообще говоря

θ1≠θ2≠ θ3≠…≠θN. Каждое из этих отклонений может быть направлено в

любую сторону относительно предшествующего. Т.к. они

статистически независимы и равновероятны по разным направлениям,

то суммарное отклонение будет равно нулю

Поэтому результирующий угол рассеяния не может служить мерой многократного рассеяния. Однако из-за того, что каждое рассеяние дает угол отклонения θi ≠ 0, то для количественного описания вводится среднеквадратичный угол многократного

Рассеяния

, так как

Ранее было получено соотношение между угловым отклонением

θ и прицельным параметром b:

. Так как для малых углов tgθ ≈ θ, то можно записать:

.

Число столкновений с параметром удара b на пути x , приводящих к отклонению на угол θ(b), равно N(b)db=2πnxbdb, а полное число столкновений на пути x будет

.

Среднее значение на пути x в результате N столкновений

можно найти следующим образом:

, и

.

Эта формула была бы совершенно точной, если бы на расстояниях, больших bmax , заряд ядра был полностью экранирован электронами атома, и рассеяния не было совсем, а для всех расстояний, меньших bmax и больших bmin , экранирование вообще бы отсутствовало. Но такой определенной границы в действительности не существует, так как с увеличением расстояния от ядра экранирование возрастает постепенно. Однако логарифмический множитель слабо зависит от величин bmax и b min , и поэтому можно положить, что bmin≈ R ядра, а bmax≈ a - радиусу атома. По порядку величины логарифмический член равен 10.

Таким образом, если скорость частицы на пути x не меняется, то

среднеквадратичный угол многократного рассеяния

В классическом случае произведение pV равно удвоенной кинетической энергии частицы. В предельно релятивистском случае Vp ≈ с·p и почти равно кинетической энергии, поэтому при грубой оценке можно считать, что

Еще раз рассмотрим формулу для угла многократного рассеяния и подставим значения для bmin и bmax:

Максимальный прицельный параметр можно оценить обычным образом bmax~aэ, где aэ – параметр экранирования. Минимальный прицельный параметр bmin можно оценить, исходя из следующего критерия: на всей толщине слоя в среднем происходит только один акт рассеяния с прицельным параметром b < bmin, т.е. N(b < bmin) = 1. Тогда

Таким образом, угол многократного рассеяния

• пропорционален заряду рассеивающейся частицы;

• пропорционален заряду рассеивающего ядра;

• обратно пропорционален энергии частицы;

• пропорционален квадратному корню из атомной плотности;

• пропорционален квадратному корню из толщины

(В нерелятивистском случае pu = 2E, а в ультрарелятивистском pu ≈ E)

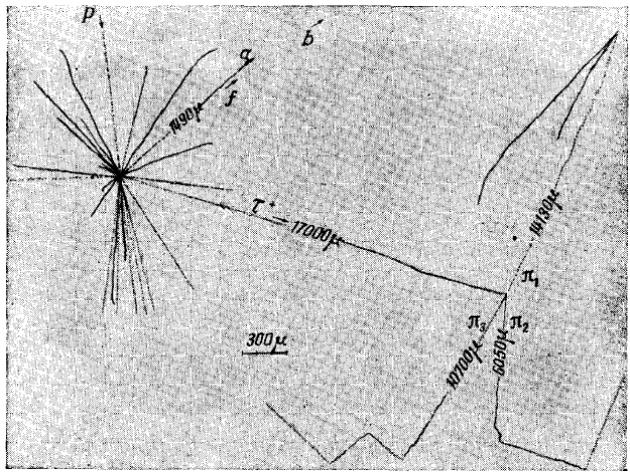
Многократное рассеяние играет большую роль при экспериментальном изучении частиц большой энергии. Измерение угла многократного рассеяния в ядерной эмульсии является эффективным методом определения энергии быстрых частиц. В других случаях как, например, при работе с вершинными детекторами

на ускорителе, необходимо учитывать многократное рассеяние, поскольку оно искажает углы вылета вторичных частиц и затрудняет кинематический анализ явления.

Многократное рассеяние было рассмотрено в рамках приближенной модели, которая тем не менее, правильно отражает основные зависимости угла многократного рассеяния от параметров частицы и среды. Более строгое рассмотрение должно учитывать эффекты экранирования (это делается, например, в рамках теории Мольер), потери энергии при достаточно толстых слоях, квантовые эффекты.

Измерение импульсов частиц методом многократного рассеяния в эмульсионных

детекторах