
- •Руководство к решению задач по алгебре
- •Часть IV Комплексные числа
- •1. Понятие комплексного числа
- •2. Операции над комплексными числами
- •3. Комплексно сопряжённые числа и их свойства
- •4. Тригонометрическая форма комплексного числа
- •5. Действия над комплексными числами в тригонометрической форме
- •6. Формула Эйлера
- •Упражнения
- •Задачи для самоподготовки
- •Литература
5. Действия над комплексными числами в тригонометрической форме
Пусть даны два
комплексных числа
![]() и
и
![]() .
.
1) Найдем произведение двух комплексных чисел:
![]()
![]()
![]()
![]() .
.
Таким образом,
![]() ,
(8)
,
(8)
то есть при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
2) Правило умножения комплексных чисел (8) автоматически распростра-няется на любое число сомножителей.
С л е д с т в и е. Если , то
![]() .
(9)
.
(9)
Иными словами, при возведении комплексного числа в степень с натуральным показателем его модуль возводится в степень с тем же показателем, а аргумент умножается на показатель степени.
Отметим частный случай формулы (9), называемый формулой Муавра.
Положим в равенстве
(9)
![]() ,
тогда
,
тогда
![]() .
(10)
.
(10)
Этой формулой можно пользоваться для выражения синусов и косинусов кратных углов через синусы и косинусы угла .
Пример.
Найдем
![]() и
и
![]() .
.
![]()
![]() .
.
Но из равенства комплексных чисел вытекает равенство действительных и мнимых частей, поэтому
![]() ,
,
![]() .
.
3) Найдем частное двух комплексных чисел:
![]()
![]() .
.
4) Найдем корень
![]() -й
степени из комплексного числа.
-й
степени из комплексного числа.
Корнем
-й
степени из комплексного числа
называется такое комплексное число
![]() ,
что
,
что
![]() .
.
Корень
-й
степени из
обозначают
![]() .
.
Покажем, что из любого комплексного числа можно извлечь корень -й степени, причем, если , то принимает ровно значений.
Такое комплексное
число
,
-я
степень которого равна
,
будем искать в тригонометрической
форме:
![]() ,
тогда
,
тогда
![]() .
.
Очевидно, что
![]() ,
,
![]()
Таким образом,
![]() ,
,
![]()
Заметим, что при
![]()
![]() ,
при
,
при
![]()
![]() ,
… , при
,
… , при
![]()
![]() ,
при
,
при
![]()
![]() ,
при
,
при
![]()
![]() ,
… . Очевидно, что все остальные значения
аргумента будут повторять уже выписанные
для
,
… . Очевидно, что все остальные значения
аргумента будут повторять уже выписанные
для
![]() с точностью до
с точностью до
![]() ,
а так как
,
а так как
![]() и
и
![]() – функции
-периодические,
то мы получим ровно
различных
значений корня.
– функции
-периодические,
то мы получим ровно
различных
значений корня.
Таким образом, корнем -й степени из комплексного числа является группа из чисел.
З а м е ч а н и е.
Точки, изображающие все получаемые
значения
![]()
![]() ,
лежат на одной окружности (центром
которой является точка
,
а радиусом – число
,
лежат на одной окружности (центром
которой является точка
,
а радиусом – число
![]() )
и делят эту окружность на
равных частей, то есть являются вершинами
правильного
-угольника.
)
и делят эту окружность на
равных частей, то есть являются вершинами
правильного
-угольника.
6. Формула Эйлера
Важную роль в математике играет формула Эйлера
![]() .
.
Применяются также формулы
![]() ,
,
![]() .
.
Упражнения
№ 103.
![]() .
Найти
.
Найти
![]() и
и
![]() ,
считая их вещественными.
,
считая их вещественными.
Раскроем скобки и приведем подобные слагаемые:
![]()
![]()
![]()
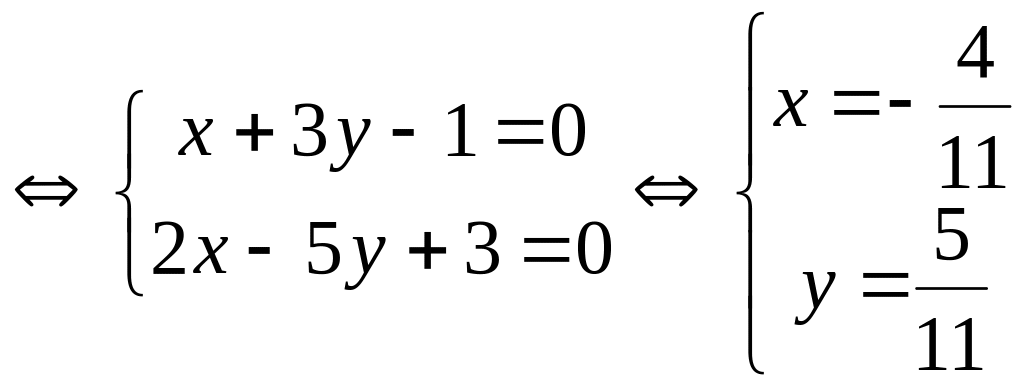 .
.
№ 107. Выполнить указанные действия:
c)
![]()
![]()
![]() .
.
№ 108. Решить системы уравнений:
a)
![]() ,
,
![]() .
.
Выразим из первого
уравнения
![]() и подставим во второе уравнение, получим
и подставим во второе уравнение, получим
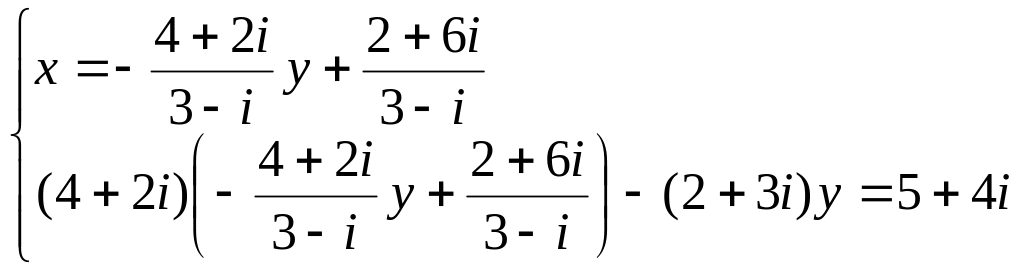
![]() .
.
№ 109. Вычислить:
b)
![]() .
.
I способ.
![]() .
.
II способ.
![]() .
.
№ 112. Вычислить:
g)
![]() .
.
Представим
![]() как
как
![]() .
Так как
.
Так как
![]() ,
то из уравнения
,
то из уравнения
![]()
следует, что

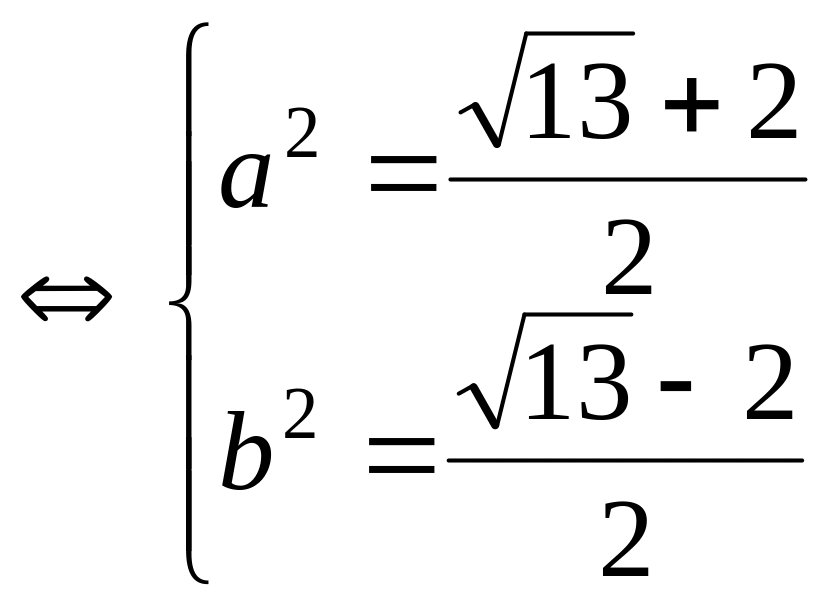
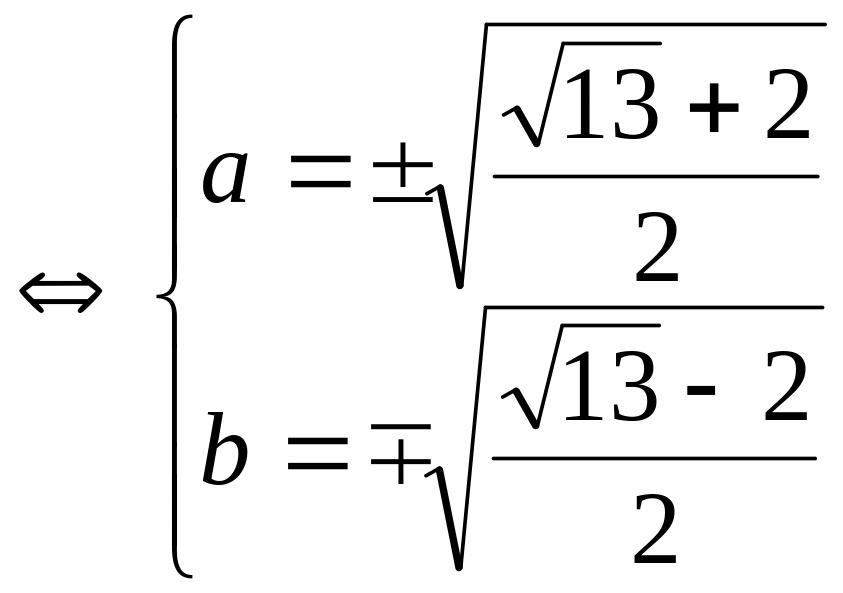 .
.
Таким образом,
получили два значения корня
![]() .
.
№ 113. Решить уравнения:
b)
![]() .
.
![]()
![]() ,
,
![]() .
.
Таким образом,
![]() ,
,
![]() .
.
с)
![]() .
.
![]()
![]() ,
,
![]() .
.
Таким образом,
![]() ,
,
![]() .
.
№ 115. Решить уравнения:
b)
![]() .
.
Сделаем замену
переменных:
![]() ,
получим
,
получим
![]() .
.
![]() ,
,
![]() .
.
Вернемся к обратной замене:
![]() .
.
№ 119. Представить в тригонометрической форме следующие числа:
a)
![]() ;
;
e)
![]() ;
;
j)
![]() .
.
№ 137. b)
Вычислить, пользуясь формулой Муавра:
![]() .
.
1) Представим сначала числитель и знаменатель дроби в тригонометрической форме:
![]() ,
,
![]() .
.
2) Дальше существуют два способа решения.
I способ. Разделим числитель на знаменатель и полученное число возведем в данную степень:

![]()
![]() .
.
II способ. Возведем числитель и знаменатель в данную степень и затем разделим:


![]() .
.
с)
![]() .
.
I способ.
![]()
![]()
![]() ;
;
![]()
![]() .
.
II способ.

![]() .
.
Таким образом,
![]() ,
,
![]() и, следовательно,
и, следовательно,
![]() ,
поэтому
,
поэтому
![]() ,
причем
,
причем
![]()
 и, следовательно,
и, следовательно,
![]() .
.
Дальнейшее решение аналогично рассмотренному ранее.
III
способ.
Воспользуемся формулами
![]() ,
,
![]() .
.
 ,
,
 .
.
Таким образом, .
Пример.
Вычислить
![]() .
.
Представим
комплексное число
![]() в тригонометрической форме. Очевидно,
что
в тригонометрической форме. Очевидно,
что
![]() ,
,
тогда
![]() ,
,
![]() .
.
При
:
![]() ;
;
:
![]() ;
;
![]() :
:
![]() ;
;
![]() :
:
![]() .
.
Таким образом,
получили 4 разных значения:
![]() .
.
№ 145. с) Вычислить
![]() .
.
1) Как и в предыдущем номере, представим числитель и знаменатель дроби в тригонометрической форме:
![]() ,
,
![]() .
.
2) Разделим числитель на знаменатель:
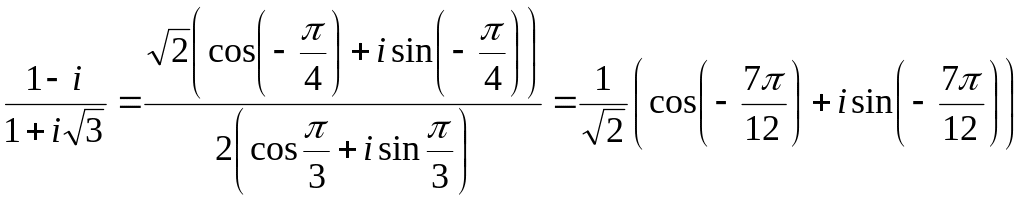 .
.
3) Извлечем корень 6-й степени из получившегося комплексного числа:
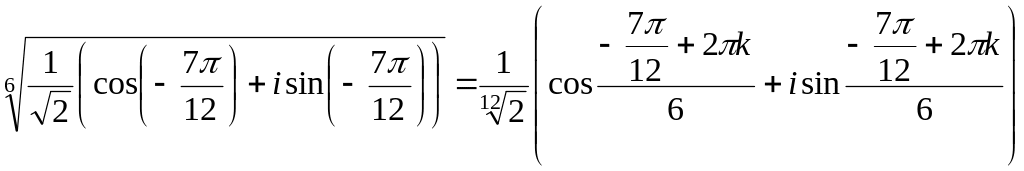 ,
,
![]()
З а м е ч а н и е. При извлечении корня -й степени из комплексного числа пункты 2 и 3 менять местами нельзя!!!
№ 143. Извлечь корни:
a)
 ,
,
![]()
При
![]() :
:
![]() ;
;
![]() :
:
![]() ;
;
![]() :
:
![]() .
.
Таким образом,
получили 3 различных значения:
![]() ,
,
![]() .
.
b)

 ,
,
![]() .
.
При
:
![]() ;
;
:
![]() ;
;
:
![]() .
.
№ 146. Выразить
через
![]() и
и
![]() :
:
a)
![]() .
.
Воспользуемся формулой Муавра (10):
![]() .
.
Для возведения выражения в 5-ю степень воспользуемся треугольником Паскаля:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Таким образом,
![]() ,
,
![]() .
.
