3. Комплексно сопряжённые числа и их свойства

Пусть нам даны два комплексных числа , . Докажем следующие свойства.

1) .

Число, комплексно сопряженное к сумме комплексных чисел, равно сумме комплексно сопряженных чисел.

Действительно, так как , то

. (2)

С другой стороны,

. (3)

Из (2), (3) и следует доказательство свойства 1.

2) .

Число, комплексно сопряженное к произведению двух комплексных чисел, равно произведению комплексно сопряженных чисел.

Действительно, так как , то

. (4) С другой стороны, так как , , то

. (5)

Из формул (4), (5) и следует доказательство свойства 2.

3) .

Число, комплексно сопряженное к частному двух комплексных чисел, равно частному комплексно сопряженных чисел.

Так как , то

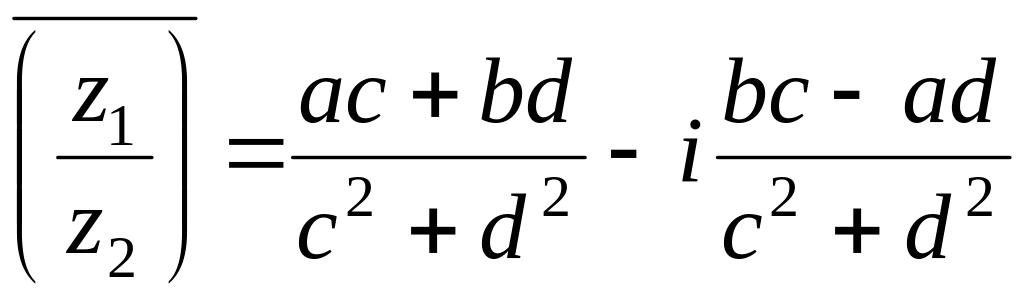. (6)

С другой стороны,

. (7)

Из формул (6), (7) следует доказательство свойства 3.

4. Тригонометрическая форма комплексного числа

На комплексной плоскости часто рассматриваются также полярные координаты. Чтобы задать полярную систему координат, выбирают точку (полюс) и выходящий из этой точки луч (полярную ось).

Модулем комплексного числа называется число .

Пусть , тогда угол между положительным направлением полярной оси и радиус-вектором числа называется аргументом

числа : , .

Угол измеряется в радианах и откладывается против часовой стрелки. Очевидно, что и, следовательно, .

Числу может быть приписан любой аргумент.

Im z

r

О Re z

З а м е ч а н и е. Пару чисел часто называют полярными координатами комплексного числа .

Таким образом, каждому комплексному числу можно поставить в соответствие пару .

Найдем связь между полярными и комплексными координатами числа . Очевидно, что , и, следовательно,

.

Запись комплексного числа в виде называется тригонометрической формой комплексного числа.

З а м е ч а н и я.

1. Аргумент комплексного числа всегда одинаковый у синуса и косинуса, его менять нельзя!

2. В тригонометрической форме комплексного числа между действительной и мнимой частями всегда стоит знак “+” !