
-
 ,
,![]()
где
в определителе под знаком суммы
![]() -я
строка – это строка
-я
строка – это строка
![]() .
Раскладывая каждый определитель под
знаком суммы по
-й
строке, получим следующую формулу
.
Раскладывая каждый определитель под
знаком суммы по
-й
строке, получим следующую формулу
![]() ,
(2.7.2.2)
,
(2.7.2.2)
где
через
![]() обозначен
определитель
обозначен
определитель
 ,
,
а
через
![]() -- алгебраическое
дополнение к элементу
-- алгебраическое
дополнение к элементу
![]() определителя
определителя
![]() .
.
Формулой (2.7.2.2) удобно пользоваться в том случае, когда путем изменения элементов определителя на одно и то же число он приводится к виду, в котором легко считать алгебраические дополнения , в частности, когда значительная их часть равна нулю.
Пример 2.7.2.1. Вычислить определитель
 .
.
Р е ш е н и е.
Обозначим
через
определитель, полученный из
вычитанием
1 из всех его элементов, т.е.
 .
.
Очевидно,
что
![]() .
Алгебраические
дополнения к внедиагональным элементам
определителя
равны нулю, а к диагональным
.
Алгебраические
дополнения к внедиагональным элементам
определителя
равны нулю, а к диагональным
![]() .
Тогда,
в силу формулы
(2.7.2.2),
.
Тогда,
в силу формулы
(2.7.2.2),
![]() .
.
Пример 2.7.2.2. Вычислить определитель
 .
.
Р е ш е н и е.
Вычитаем
из всех элементов определителя величину
![]() и обозначаем через
определитель
и обозначаем через
определитель
 .
.
Очевидно,
что
![]() ,
алгебраические дополнения к
внедиагональ-ным элементам, как и в
примере 2.7.2.1, равны нулю, а к диагональным
,
алгебраические дополнения к
внедиагональ-ным элементам, как и в
примере 2.7.2.1, равны нулю, а к диагональным
![]() .
Таким образом,
.
Таким образом,
![]() .
.
Упражнения.
Вычислить определители
1) ;
2)
;
2) ;
;
3) ; 4)
; 4) ;
;
5) ;
6)
;
6) ;
;
7) ;
8)
;
8) .
.
2.7.3. Метод выделения линейных множителей
Пусть элементы определителя -– многочлены от одной или нескольких переменных. При преобразованиях выясняется, что определитель делится на ряд линейных множителей. Находим частное от деления определителя и тем самым получаем выражение определителя.
Пример 2.7.3.1. Вычислить определитель
 .
(2.7.3.1)
.
(2.7.3.1)
Р е ш е н и е.
Прибавив к первой строке вторую, третью и четвертую строку, получим, что
 .
.
Вычтем из первой строки вторую и четвертую, прибавим третью. Получим, что
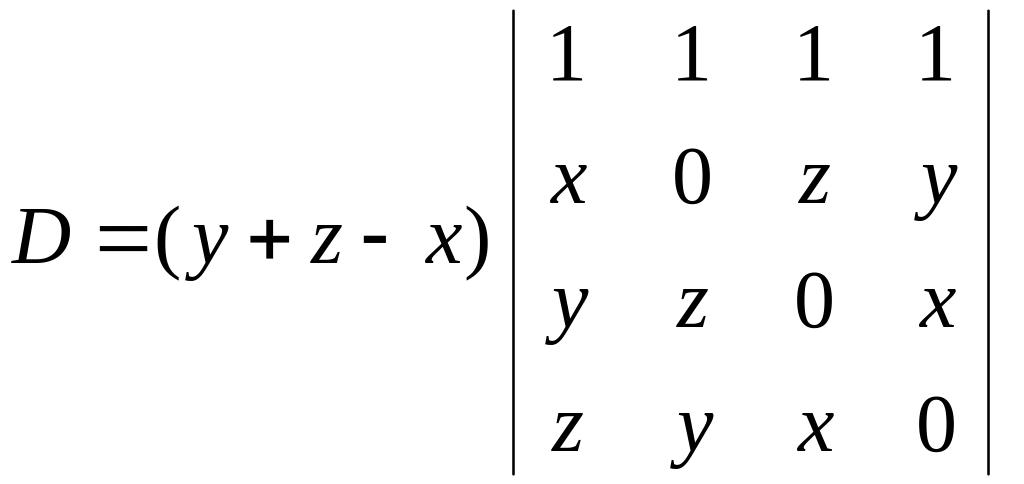 .
.
Прибавляя к первой строке третью и вычитая вторую и четвертую, получим
 .
.
Наконец, прибавляя к первой строке четвертую и вычитая вторую и третью, видим, что
 .
.
Так
как
![]() – независимые переменные и множители
– независимые переменные и множители
![]() ,
,
![]() ,
,
![]() ,
,
![]() взаимно
простые, то определитель (2.7.3.1) делится
на их произведение.
Это произведение
содержит член
взаимно
простые, то определитель (2.7.3.1) делится
на их произведение.
Это произведение
содержит член
![]() .
Значит,
.
Значит,
![]() .
.
Пример 2.7.3.2. Вычислить определитель
 .
(2.7.3.2)
.
(2.7.3.2)
Р е ш е н и е.
Определитель
(2.7.3.2) является многочленом от переменной
.
Корнями этого многочлена являются те
значения
,
при которых определитель (2.7.3.2) равен
нулю. При
![]() в (2.7.3.2.) совпадают 1-я и 2-я строки, а
значит, определитель (2.7.3.2) делится на
в (2.7.3.2.) совпадают 1-я и 2-я строки, а
значит, определитель (2.7.3.2) делится на
![]() ,
так как
– корень многочлена. При
,
так как
– корень многочлена. При
![]() в (2.7.3.2) совпадают 1-я и 3-я строки, а
значит, исходный определитель делится
на
в (2.7.3.2) совпадают 1-я и 3-я строки, а
значит, исходный определитель делится
на
![]() ,
и т.д. Таким образом, (2.7.3.2) делится на
,
и т.д. Таким образом, (2.7.3.2) делится на
![]() .
Очевидно, что коэффициент при старшей
степени
многочлена
равен
1.
Таким
образом,
.
Очевидно, что коэффициент при старшей
степени
многочлена
равен
1.
Таким
образом,
![]() .
.
У п р а ж н е н и я.
Вычислить следующие определители методом выделения линейных множителей :
1) ;
2)
;
2) ;
;
3) ;
4)
;
4) ;
;
5) ;
6)
;
6) ;
;
7) ;
8)
;
8) ;
;
9) ;
10)
;
10) ;
;
11) ;
12)
;
12) .
.
Метод рекуррентных соотношений
Суть
метода рекуррентных соотношений
заключается в том, что данный определитель
![]() -го
порядка выражают, преобразуя и разлагая
его по строке или столбцу, через
определители того же вида, но более
низкого порядка. Полученное равенство
называется
рекуррентным
или
возвратным
соотношением.
-го
порядка выражают, преобразуя и разлагая
его по строке или столбцу, через
определители того же вида, но более
низкого порядка. Полученное равенство
называется
рекуррентным
или
возвратным
соотношением.
Этот способ можно
видоизменить следующим образом. В
рекуррентное соотношение, выражающее
определитель
-ого
порядка через определители низшего
порядка, подставляют выражение
определителя
![]() -го
порядка, получающегося заменой
на
,
затем подобным образом подставляют
выражение определителя
-го
порядка, получающегося заменой
на
,
затем подобным образом подставляют
выражение определителя
![]() -го
порядка и т.д., пока не придем к общему
выражению данного определителя
-го
порядка.
-го
порядка и т.д., пока не придем к общему
выражению данного определителя
-го
порядка.
Пример 2.7.4.1.
Вычислить
определитель
![]() -го
порядка
-го
порядка
 .
(2.7.4.1)
.
(2.7.4.1)
Р е ш е н и е.
Разложим определитель
![]() по последней
строке
по последней
строке

или
![]() .
(2.7.4.2)
.
(2.7.4.2)
Теперь вычислим
определитель (2.7.4.1), пользуясь формулой
(2.7.4.2). Для
![]()
![]() ,
для
,
для
![]()
![]() .
Положим,
что
.
Положим,
что
![]() .
.
Предположим, что
![]() .
В силу (2.7.4.2) имеем
.
В силу (2.7.4.2) имеем
![]()
![]()
Пример 2.7.4.2. Вычислить определитель -ого порядка
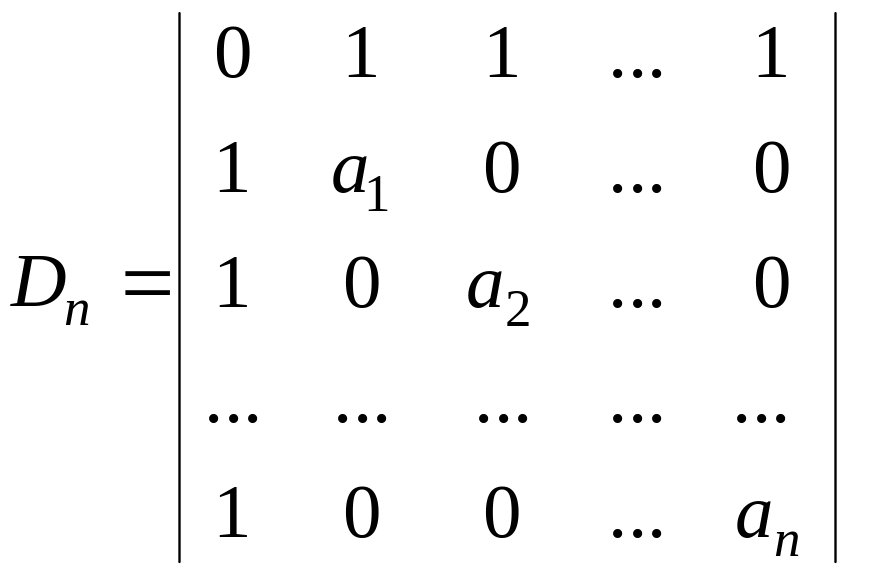 .
.
Р е ш е н и е.
Разложим
![]() по последней
строке, получим
по последней
строке, получим
 (2.7.4.3)
(2.7.4.3)
 .
.
