
- •Руководство к решению задач по алгебре
- •Часть I
- •§1. Матрицы (действия над ними, обратная матрица)
- •1.1. Действия над матрицами
- •1.1.1. Сложение и умножение на число
- •1.1.2. Умножение матриц
- •1.1.3. Многочлен от матрицы
- •Обратная матрица
- •§2. Определители: определение, свойства и вычисление
- •Понятие перестановки, подстановки, инверсии, транспозиции
- •Определители второго и третьего порядков
- •По правилу треугольника:
1.1.3. Многочлен от матрицы
Определение 14. Пусть дан многочлен
![]() и пусть
и пусть
![]() – квадратная матрица, тогда значением
многочлена
– квадратная матрица, тогда значением
многочлена
![]() от матрицы
называется матрица
от матрицы
называется матрица
![]() ,
где
,
где
![]() – единичная матрица,
– единичная матрица,
![]() – матрица, получающаяся при умножении
матрицы
на себя
раз.
– матрица, получающаяся при умножении
матрицы
на себя
раз.
№ 827 (П).
Найти значение многочлена
![]() от матрицы
от матрицы
 .
.
Р е ш е н и е.
Найдем
![]() .
.

 ;
;
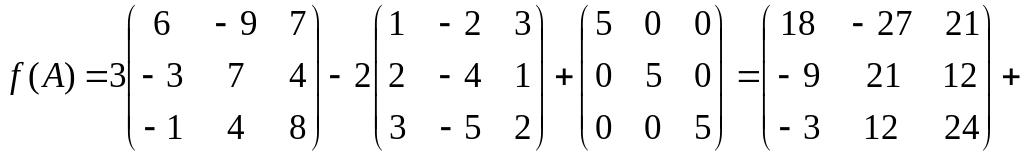
 .
.
Ответ:
 .
.
Обратная матрица
Определение 15. Матрица
![]() называется обратной к квадратной
матрице
,
если
называется обратной к квадратной
матрице
,
если
![]() .
.
Определение 16. Квадратная матрица
называется невырожденной, если
она имеет единственную обратную матрицу
![]() .
В противном случае
– вырожденная матрица.
.
В противном случае
– вырожденная матрица.
Утверждение. Квадратная матрица порядка является невырож-денной в том и только том случае, если определитель этой матрицы отличен от нуля.
Для отыскания обратной матрицы существуют два способа.
Припишем к матрице справа единичную матрицу и, применяя метод Гаусса (см. §5), преобразуем расширенную матрицу так, чтобы слева стояла единичная матрица, тогда справа будет находиться обратная матрица
 :
:
 .
.
 .
.
Обоснование этого способа состоит в следующем.
Пусть нам дана невырожденная квадратная
матрица. Задачу нахождения обратной
матрицы можно рассматривать как задачу
решения матричного уравнения
![]() ,
которое эквивалентно системе
,
которое эквивалентно системе
![]() уравнений с
неизвестными.
уравнений с
неизвестными.
Эта система является объединением
систем уравнений, каждая из которых
содержит
неизвестных. Умножая поочередно строки
матрицы
на 1-й столбец матрицы
![]() и приравнивая к 1-му столбцу матрицы
,
получим систему уравнений, матричная
форма записи которой имеет вид
и приравнивая к 1-му столбцу матрицы
,
получим систему уравнений, матричная
форма записи которой имеет вид
 (1.2.1)
(1.2.1)
С помощью элементарных операций над строками матрицы систему уравнений можно привести к виду
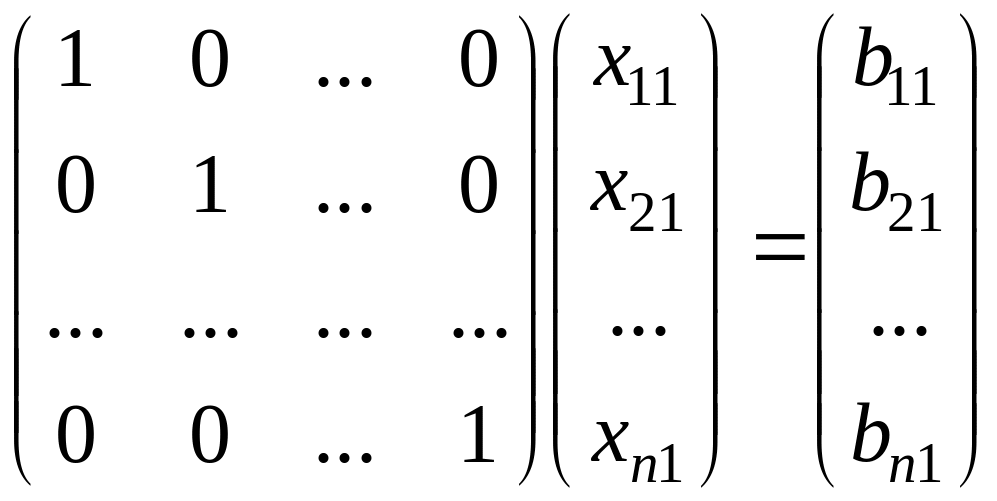
Умножая поочередно строки матрицы на второй столбец матрицы и приравняв ко второму столбцу матрицы , получим систему уравнений
 .
(1.2.2)
.
(1.2.2)
С помощью тех же элементарных операций, что применялись для решения системы (1.2.1), мы приведем систему (1.2.2) к виду

и т.д.
Поэтому для нахождения обратной матрицы и был предложен описанный выше способ.
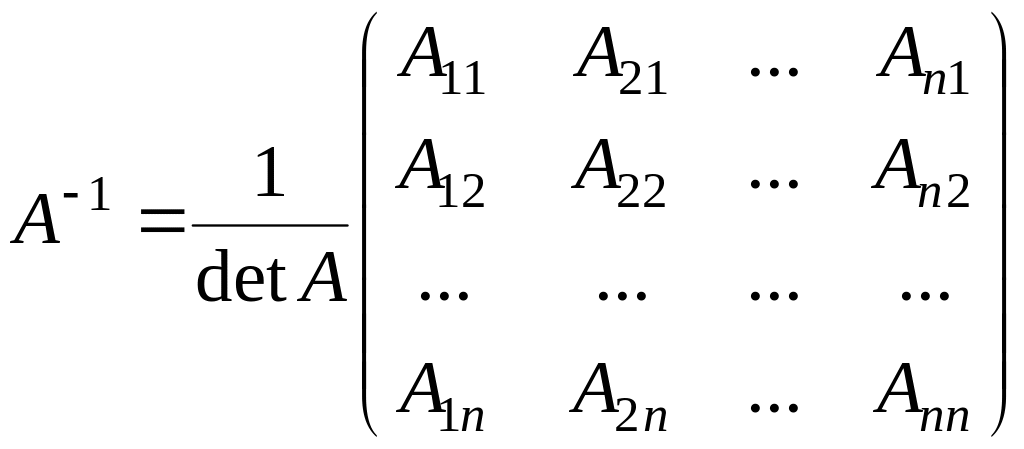 ,
где
,
где

 – алгебраические дополнения к элементу
,
– алгебраические дополнения к элементу
,
 – определитель матрицы
(см. §2).
– определитель матрицы
(см. §2).
№ 840 (П).
Найти обратную матрицу для матрицы
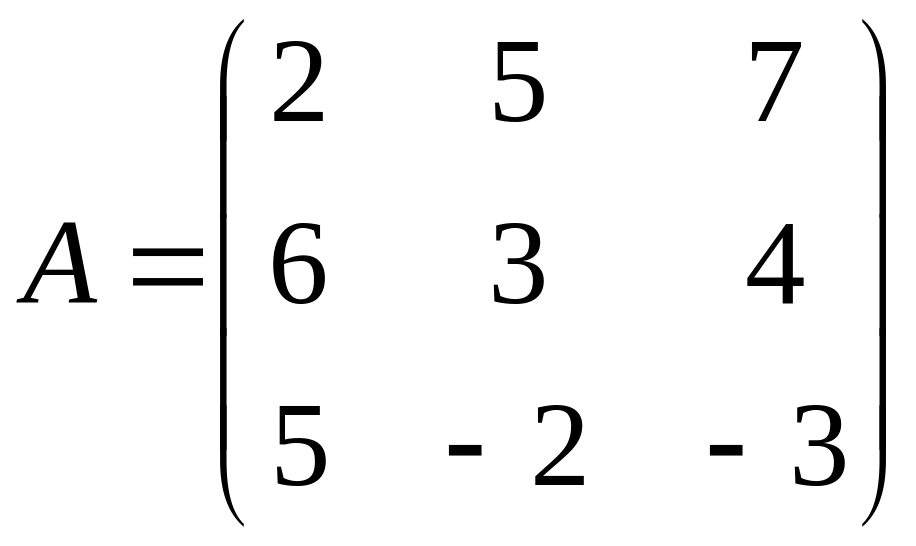 .
.
Р е ш е н и е.
I
способ.



 .
.
Ответ:
 .
.
II способ.

![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом,
 .
.
Ответ: .
№ 861 (П).
Решить матричное уравнение
![]() .
.
Р е ш е н и е.
1 вариант.
Пусть
![]() ,
тогда
,
тогда
![]()
![]()
![]()
 .
.
![]()
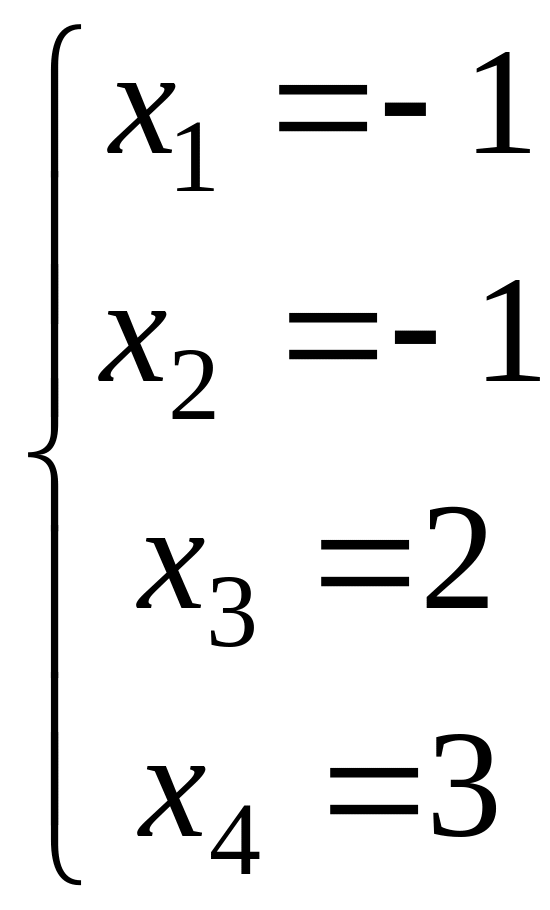 .
.
Ответ:
![]() .
.
2 вариант.
Очевидно, что
![]() .
Найдем матрицу, обратную к матрице
.
Найдем матрицу, обратную к матрице
![]() .
.
I способ:
![]()
 .
.
II способ:
 .
.
Таким образом,
 .
.
Ответ:
![]() .
.
