§ 2. Жорданова форма матрицы

1. Оператор простой структуры

В данном параграфе предлагается способ нахождения жордановой формы матрицы, основанный на изучении геометрических характеристик линейного оператора.

Дадим ряд определений.

Определение 1. Линейный оператор в пространстве называется оператором простой структуры, если он имеет линейно независимых собственных векторов.

Теорема. Оператор простой структуры однозначно определен, если заданы его линейно независимых собственных векторов и соответствующие им собственные значения.

Д о к а з а т е л ь с т в о.

Выберем в качестве базиса в пространстве собственные векторы оператора . Тогда получим

,

,

……….

.

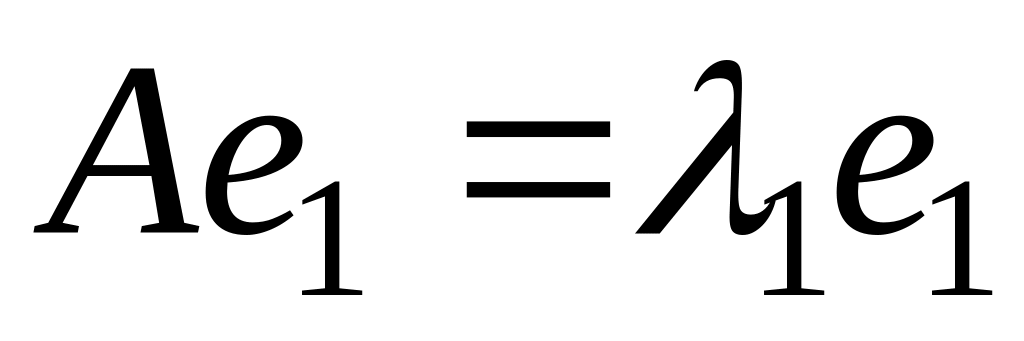Это означает, что матрица оператора (которую мы обозначим через ) имеет вид

.

Следовательно, оператор однозначно определен, а его матрица относительно базиса из собственных векторов является диагональной. Отметим, что среди чисел могут быть одинаковые. Обозначим через матрицу оператора в базисе из векторов . Тогда