
- •Руководство к решению задач по алгебре
- •Часть II Жорданова форма матрицы и жорданов базис
- •§1. Собственные векторы и собственные значения оператора.
- •Рассмотрим линейный оператор в пространстве и пусть – матрица этого оператора в некотором базисе .
- •1.2. Алгебраическая и геометрическая кратности собственного значения
- •Жорданова форма матрицы и жорданов базис
- •Алгоритм нахождения жорданова базиса для одной жордановой клетки
- •Алгоритм нахождения жордановой формы и жорданова базиса для матрицы 3-го порядка
- •1.5. Функции от матриц
- •§ 2. Жорданова форма матрицы
- •Оператор простой структуры
1.5. Функции от матриц
N 1162.
Вычислить
,
если
![]() .
.
Р е ш е н и е.
Найдем характеристический многочлен матрицы :
![]() ,
,
поэтому
жорданова форма матрицы
![]() и, следовательно,
и, следовательно,
![]() .
.
Заметим, что
![]()
![]() (1.2)
(1.2)
Таким образом, нам нужно найти матрицу перехода от исходного базиса к жорданову. Для этого найдем жорданов базис.
При
![]() получим
получим
![]() и, следовательно,
и, следовательно,
![]() ;
при
получим
;
при
получим
![]() ,
поэтому
,
поэтому
![]() и
и
![]() .
.
Осталось
найти матрицу
![]() и воспользоваться формулой (1.2).
и воспользоваться формулой (1.2).
N
1163.
Вычислить
![]() ,
если
,
если
![]() .
.
Найдем характеристический многочлен матрицы :
![]() ,
,
поэтому
,
![]() .
.
Найдем геометрическую кратность собственного значения :
![]() ,
(1.3)
,
(1.3)
следовательно,
![]() и
и
![]() .
.
Докажем,
что
![]() ,
пользуясь методом математической
индукции.
,
пользуясь методом математической
индукции.
Очевидно,
что при
![]() .
.
Пусть это утверждение истинно для
![]() ,
то есть
,
то есть
![]() .
.
Докажем его для
![]() .
.
Действительно,
![]() .
.
Таким образом,
![]() ,
,
поэтому
![]() .
.
Найдем
жорданов базис. Из (1.3) следует, что
![]() .
Найдем
из уравнения
.
Найдем
из уравнения
![]() ,
откуда следует, что
,
откуда следует, что
![]() ,
и, следовательно,
,
и, следовательно,
![]() .
.
Подставляя
![]() ,
и
,
и
![]() в формулу (1.4), получим
.
в формулу (1.4), получим
.
Утверждение 1. Если матрица подобна диагональной

и
для функции
![]() матрица
матрица
![]() существует, то и
подобна диагональной матрице, причем
существует, то и
подобна диагональной матрице, причем
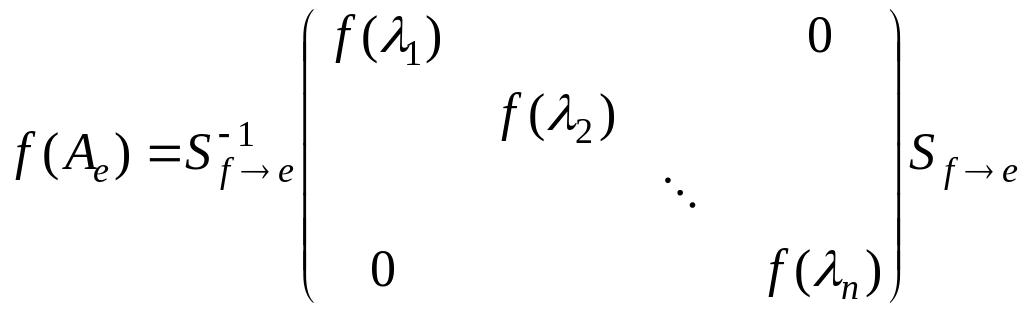
с той же матрицей .
N
1166. Вычислить
![]() ,
где
,
где
![]() .
.
Р е ш е н и е.
Найдем характеристический многочлен матрицы :
![]()
следовательно,
![]() ,
,
![]() ,
поэтому
,
поэтому
![]() ,
,
![]() .
.
Найдем собственные векторы оператора .
Так как
![]() ,
,
то
координаты собственного вектора,
отвечающего собственному значению
,
удовлетворяют соотношению
![]() ,
поэтому
,
поэтому
![]() .
.
Аналогично
![]() ,
откуда
,
откуда
![]() ,
поэтому
,
поэтому
![]() .
.
Таким
образом,
![]() и, следовательно,
и, следовательно,
![]() .
.
Поэтому
![]()
Утверждение
2. Значение
многочлена
![]() от клетки Жордана
порядка
с числом
на главной диагонали
от клетки Жордана
порядка
с числом
на главной диагонали
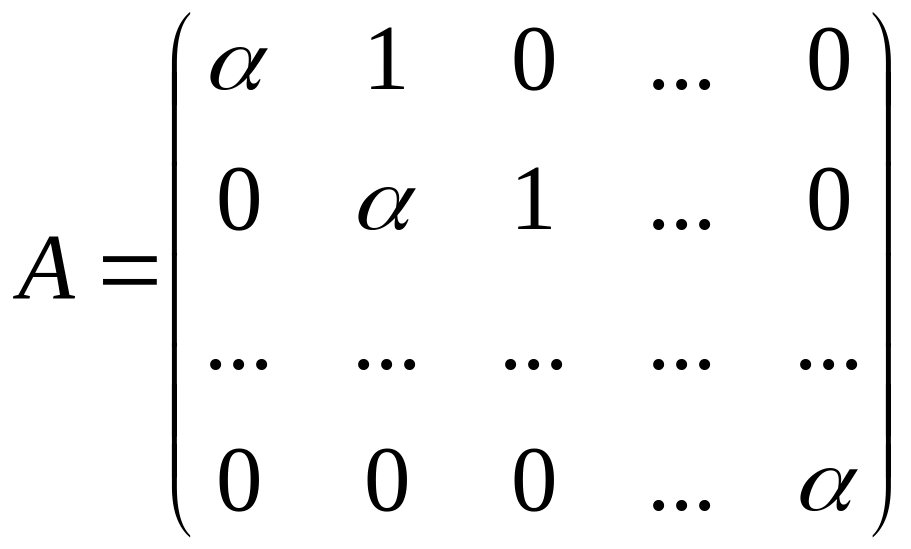
определяется формулой
 .
.
Утверждение 3. Если матрица клеточно-диагональная
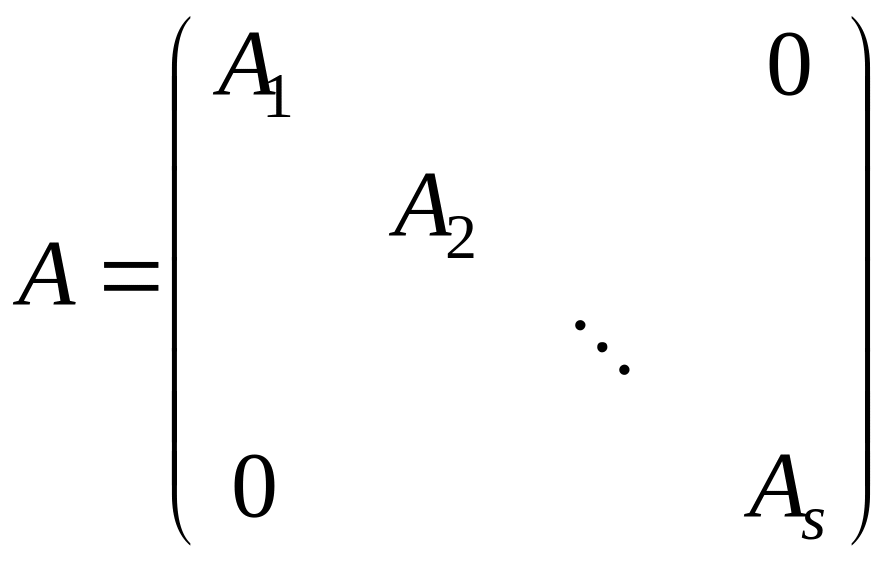
и функция определена на спектре матрицы , то
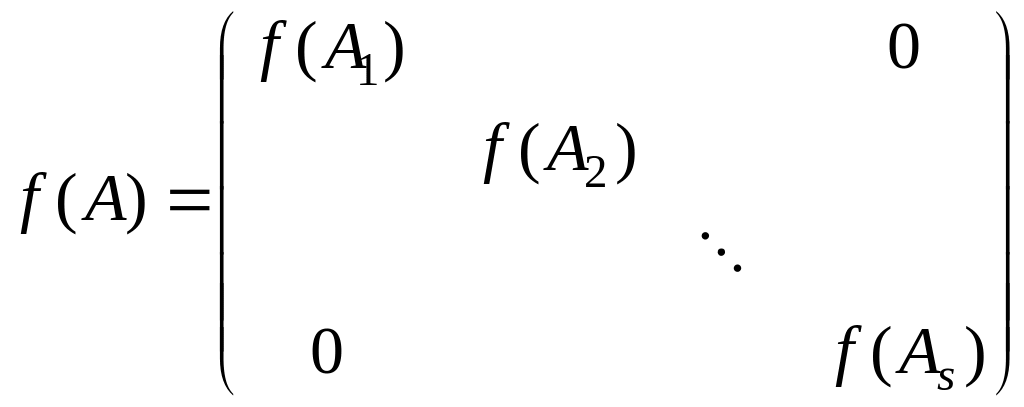 .
.
Утверждение
4. Если
матрица
подобна клеточно-диагональной матрице
![]()
![]() ,
,
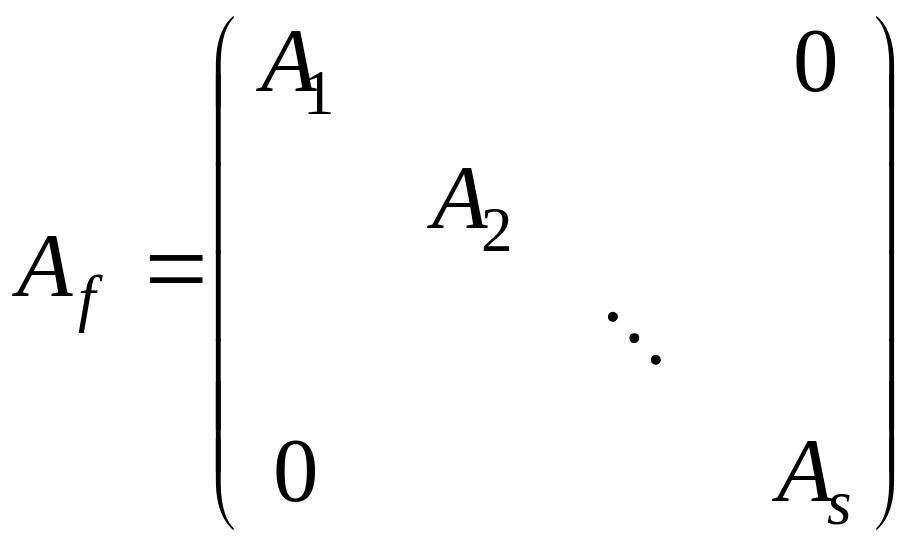 ,
,
и функция определена на спектре матрицы , то
![]()
с той же матрицей .
N
1164.
Вычислить
![]() ,
где
,
где
![]() .
.
Р е ш е н и е.
Найдем характеристический многочлен матрицы :
![]()
следовательно,
![]() ,
.
Найдем геометрическую кратность
собственного значения
,
.
Найдем геометрическую кратность
собственного значения
![]() :
:
![]() .
.
Следовательно,
и
![]() .
.
Из
утверждения 2 следует, что
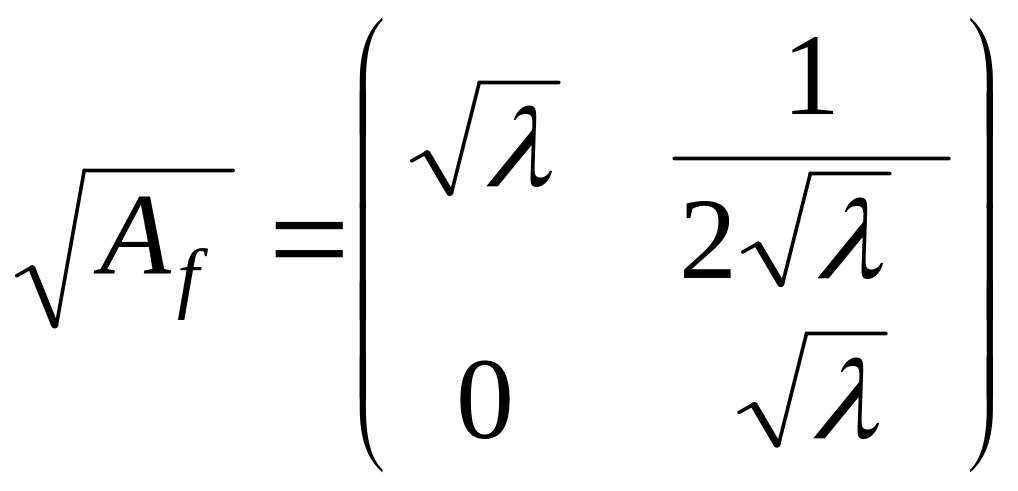 .
Так как
,
то
.
Так как
,
то

и, следовательно,
![]() .
.
Найдем жорданов базис матрицы оператора .
Так как
![]() ,
,
то
координаты собственного вектора,
отвечающего собственному значению
,
удовлетворяют соотношению
![]() ,
поэтому
,
поэтому
![]() .
.
Найдем
присоединенный вектор
из уравнения
![]() ,
откуда следует, что
и, следовательно,
,
откуда следует, что
и, следовательно,
,
![]() .
.
Таким образом,
![]() .
.
