3. Алгоритм нахождения жордановой формы и жорданова базиса для матрицы 3-го порядка

Пусть дана матрица 3-го порядка. Надо найти жорданову форму и жорданов базис.

1. Пусть характеристический многочлен матрицы имеет вид

, где .

Тогда жорданова форма матрицы имеет вид .

2. Пусть характеристический многочлен матрицы имеет вид

,

где . Возможны два случая:

а) , поэтому и, следовательно, , поэтому жорданова форма содержит две жордановы клетки с собственным значением : ;

б) , поэтому и, следовательно, жорданова форма содержит одну жорданову клетку с собственным значением : .

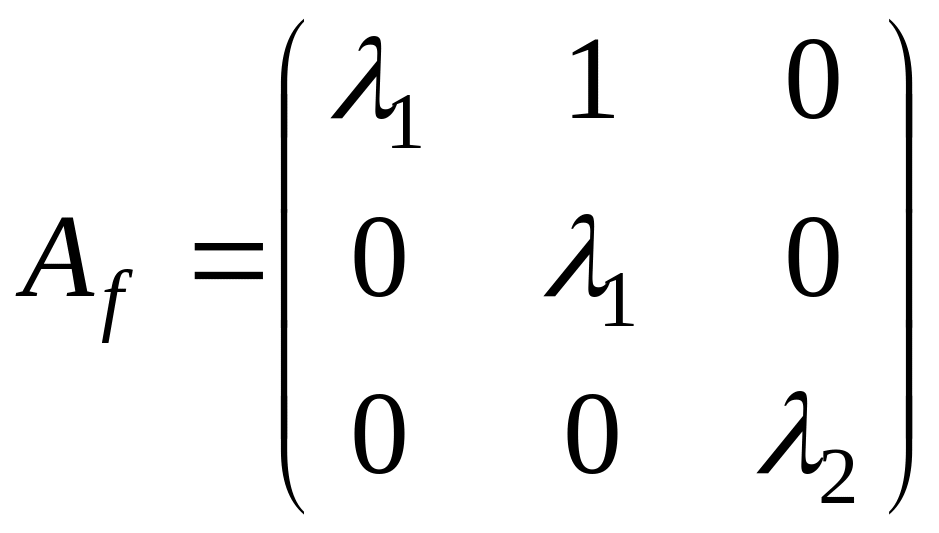3. Пусть характеристический многочлен матрицы имеет вид

.

Возможны два случая:

а) , поэтому и, следовательно, жорданова форма содержит две жордановы клетки с собственным значением : ;

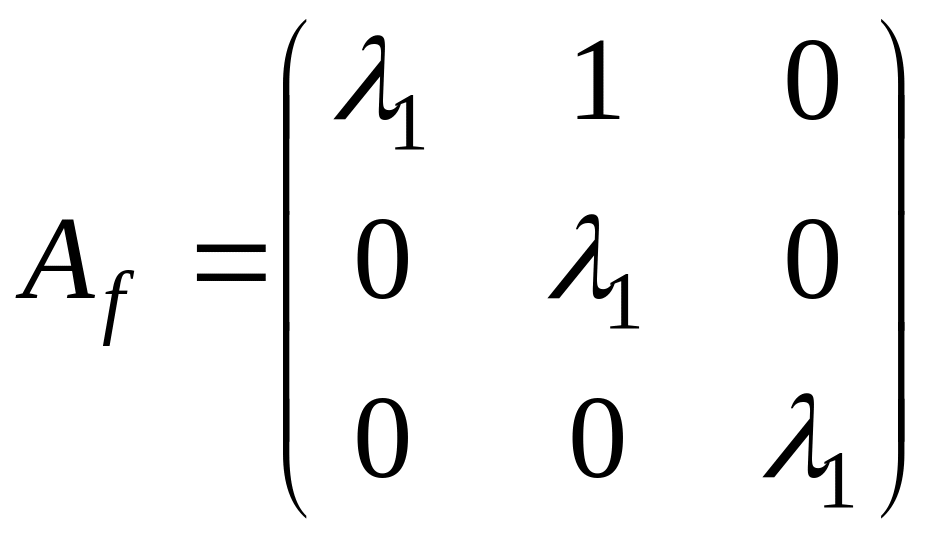б) , поэтому и, следовательно, жорданова форма содержит одну жорданову клетку с собственным значением : .

Задача. Дана матрица 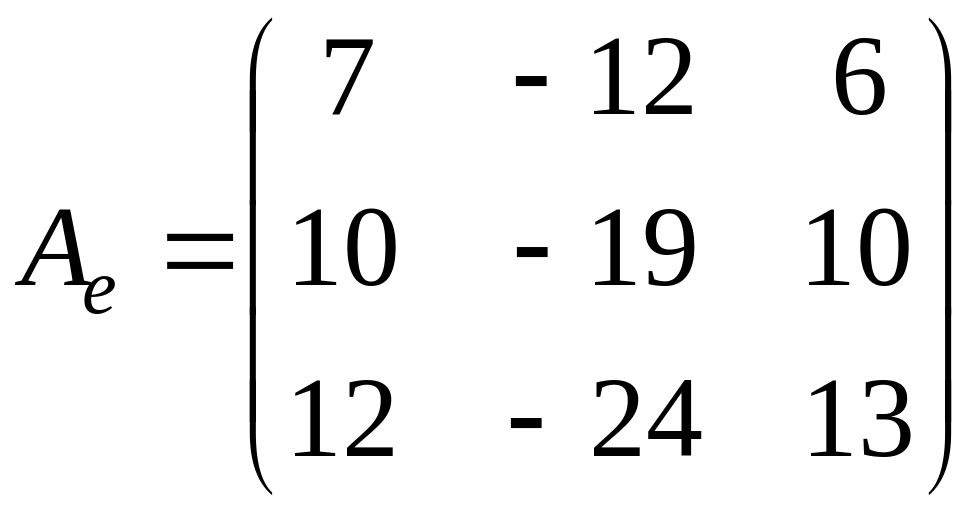. Найти .

Р е ш е н и е.

Найдем характеристический многочлен матрицы:

.

Жорданова форма матрицы имеет вид .

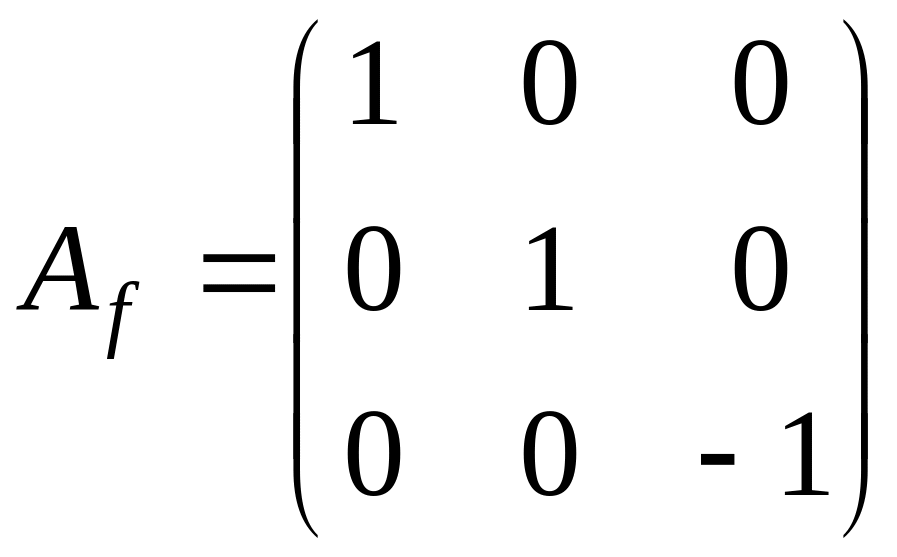Найдем

.

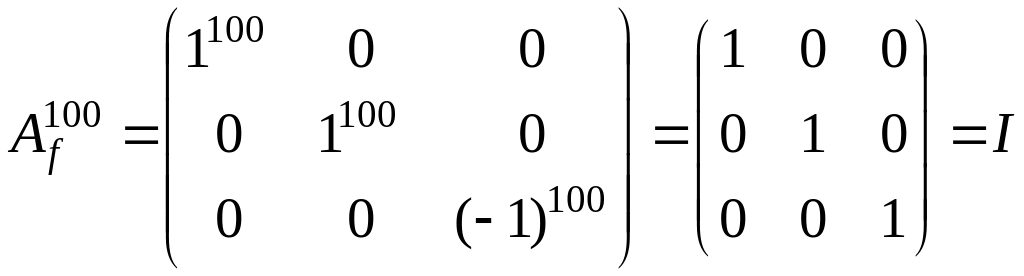Для нахождения воспользуемся формулой , где – матрица перехода от базиса к базису . Очевидно, что

,

поэтому

.

Пример 1. Найти жорданову форму и жорданов базис матрицы оператора

.

Р е ш е н и е.

Вычислим

,

следовательно, собственное значение , .

Найдем геометрическую кратность собственного значения . Для этого посчитаем ранг матрицы

.

Следовательно,

,

поэтому жорданова форма имеет вид

или .

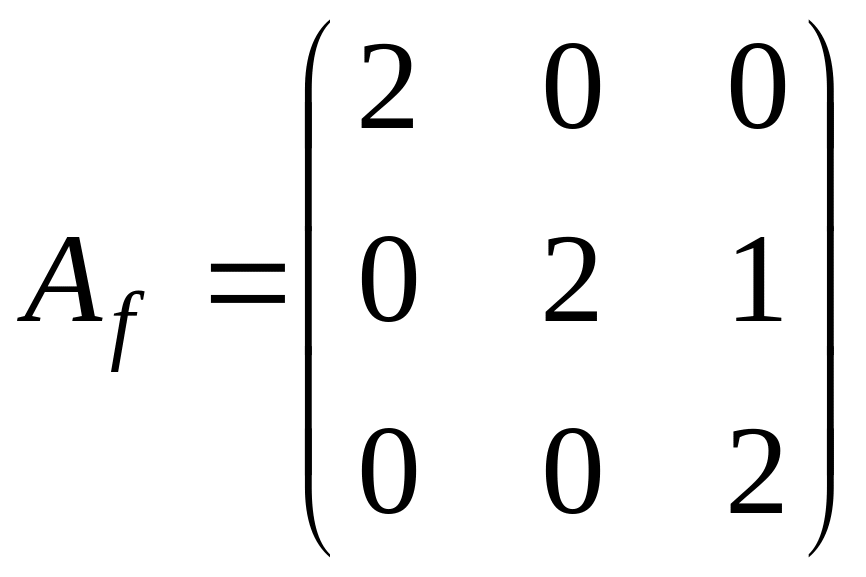Найдем собственный вектор , соответствующий собственному значению . Так как он удовлетворяет условию

,

то решим систему

.

Следовательно, координаты собственного вектора удовлетворяют уравнению

.

Заметим, что коэффициент при равен 0, поэтому может принимать любые значения. Отбрасывать нельзя !!!

Для нахождения ФСР построим таблицу

.

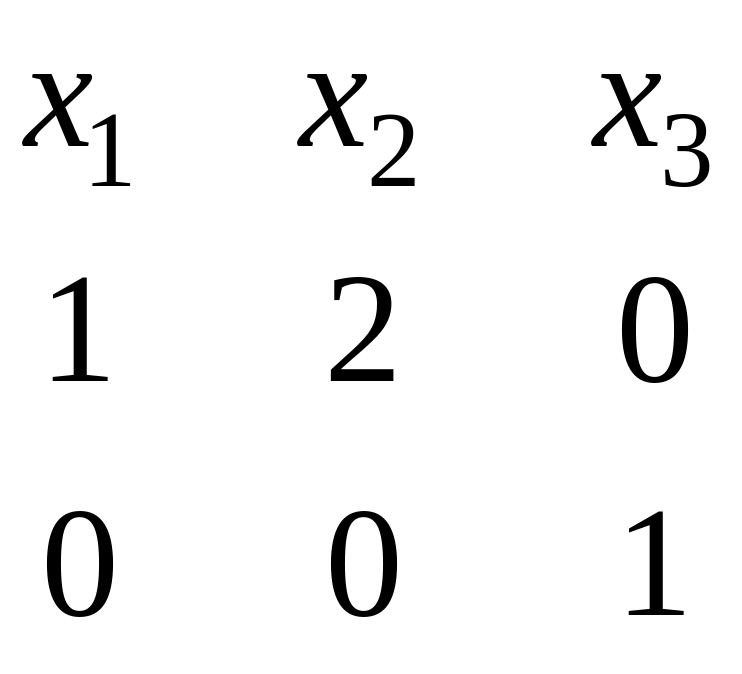Векторы , образуют фундаментальную систему решений в собственном подпространстве , поэтому любой собственный вектор, отвечающий собственному значению , линейно через них выражается и, следовательно, имеет вид . Так как , , то должен быть один присоединенный вектор, который будет являться решением системы . Подберем коэффициенты и таким образом, чтобы система была совместна. Так как

,

то для совместности системы необходимо, чтобы выполнялось условие . Возьмем , тогда , и координаты присоединенного вектора являются решением системы

,

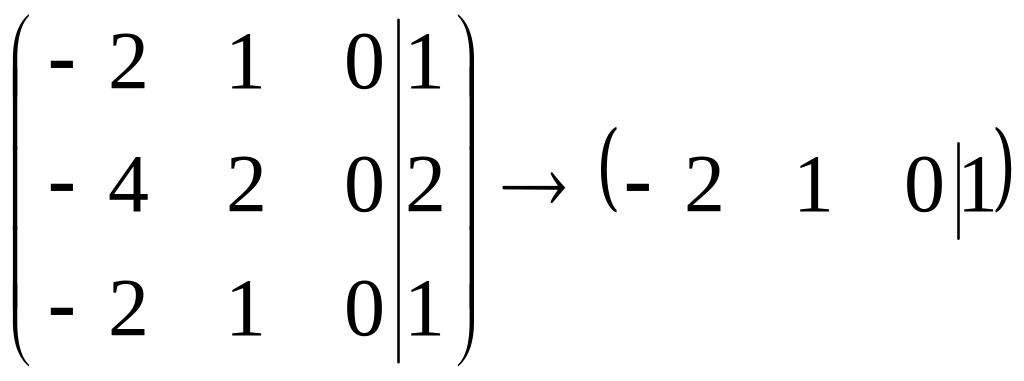то есть удовлетворяют уравнению

или .

Возьмем .

Таким образом, у нас есть собственный вектор , присоединенный к нему и нужен еще один собственный вектор, отвечающий собственному значению . Можно взять или вектор , или , или любой другой, отличный от , отвечающий собственному значению . Эти три вектора и будут образовывать жорданов базис.

Пример 2. Найти жорданову форму и жорданов базис матрицы оператора

.

Р е ш е н и е.

Вычислим

,

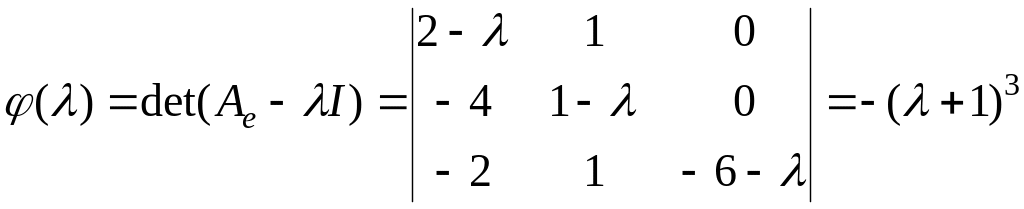следовательно, собственное значение , .

Найдем геометрическую кратность собственного значения . Для этого посчитаем ранг матрицы

.

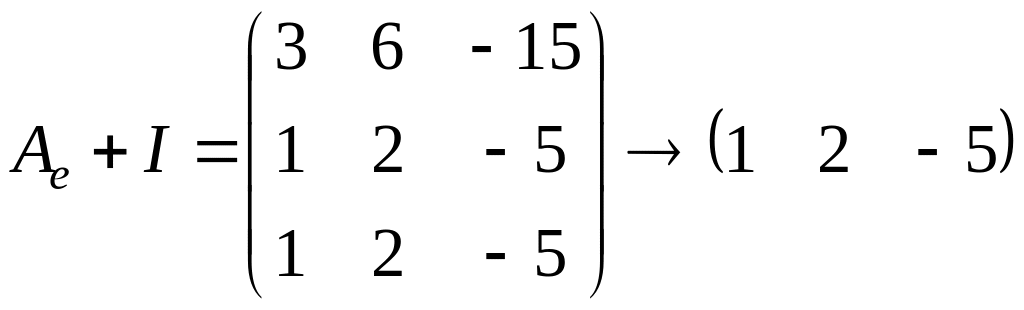Следовательно,

,

поэтому жорданова форма имеет вид

или .

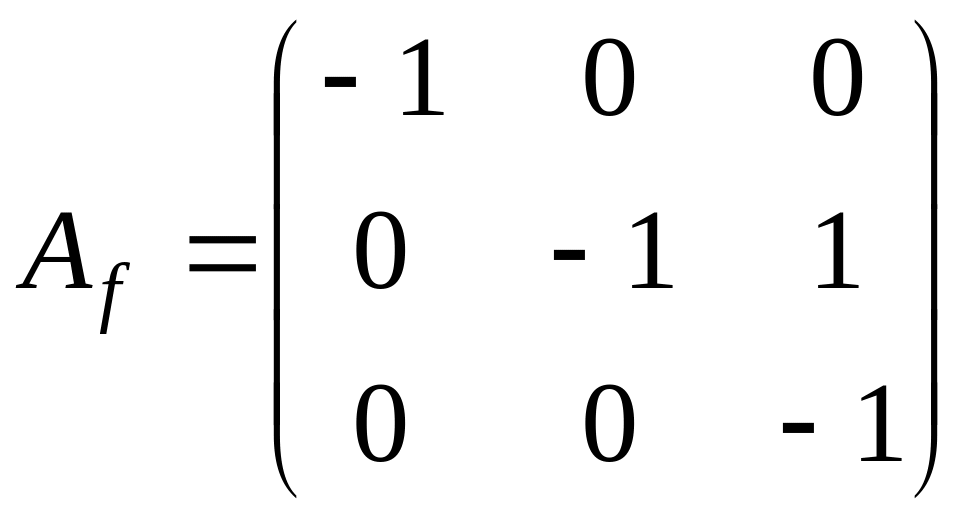Найдем собственный вектор , соответствующий собственному значению . Так как он удовлетворяет условию

,

то решим систему

.

Очевидно, что координаты собственного вектора удовлетворяют уравнению

или .

Для нахождения ФСР построим таблицу

.

Векторы , образуют фундаментальную систему решений в собственном подпространстве , поэтому любой собственный вектор, отвечающий собственному значению , линейно через них выражается и, следовательно, имеет вид

.

Так как , , то должен быть один присоединенный вектор, который будет являться решением системы . Подберем коэффициенты и таким образом, чтобы система была совместна. Так как

,

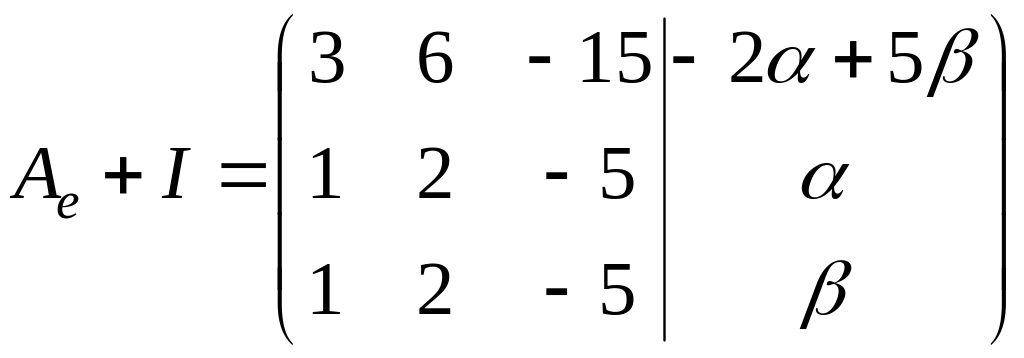то для совместности системы необходимо, чтобы выполнялось условие . Возьмем , тогда и координаты присоединенного вектора являются решением системы

,

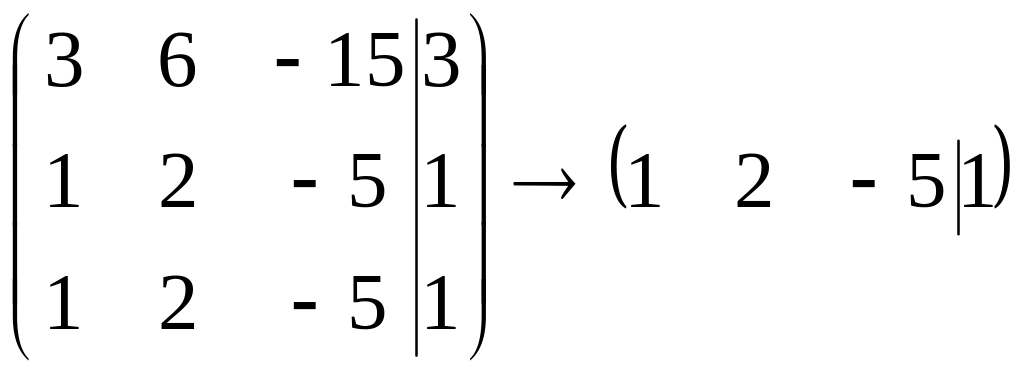то есть удовлетворяют уравнению

или .

Возьмем .

Таким образом, у нас есть собственный вектор , присоединенный к нему и нужен еще один собственный вектор, отвечающий собственному значению . Можно взять или вектор , или , или любой другой, отличный от , отвечающий собственному значению . Эти три вектора и будут образовывать жорданов базис.

Пример 3. Найти жорданову форму и жорданов базис матрицы оператора

.

Р е ш е н и е.

Вычислим

.

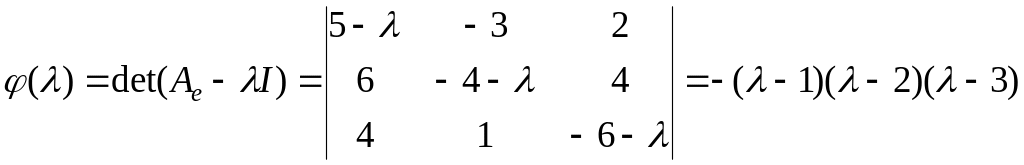Таким образом, получили три собственных значения , , . Так как алгебраическая кратность каждого из них равна 1, то жорданова форма имеет следующий вид

.

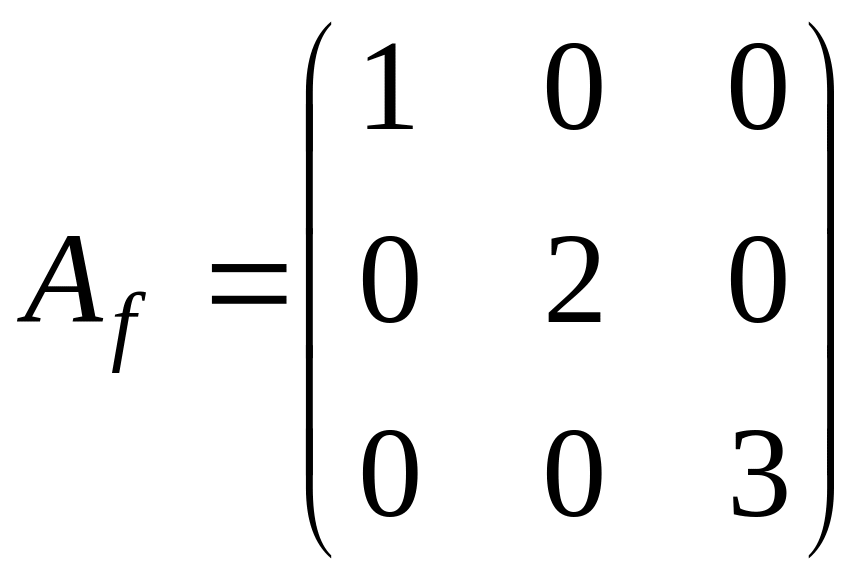Найдем собственный вектор , соответствующий собственному значению . Очевидно, что он является решением уравнения и, следовательно, его координаты удовлетворяют системе

,

то есть , поэтому можем взять .

Вычислим собственный вектор , соответствующий собственному значению . Очевидно, что он удовлетворяет уравнению , а его координаты – системе

,

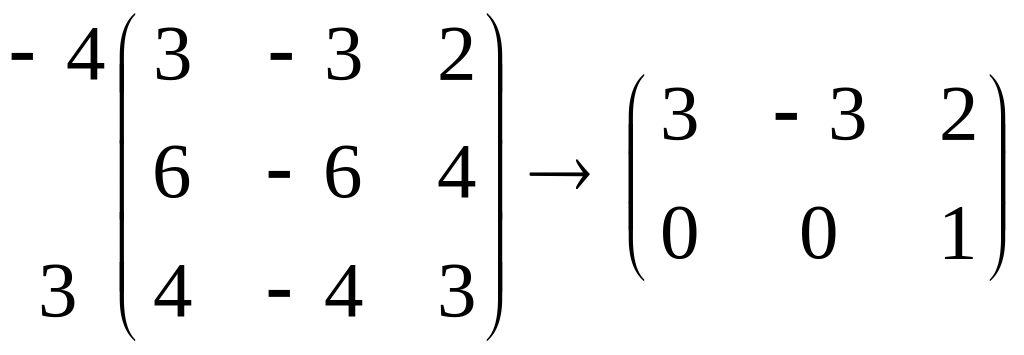откуда следует, что , поэтому можем взять .

Найдем собственный вектор , соответствующий собственному значению . Так как он является решением уравнения , то его координаты удовлетворяют системе

,

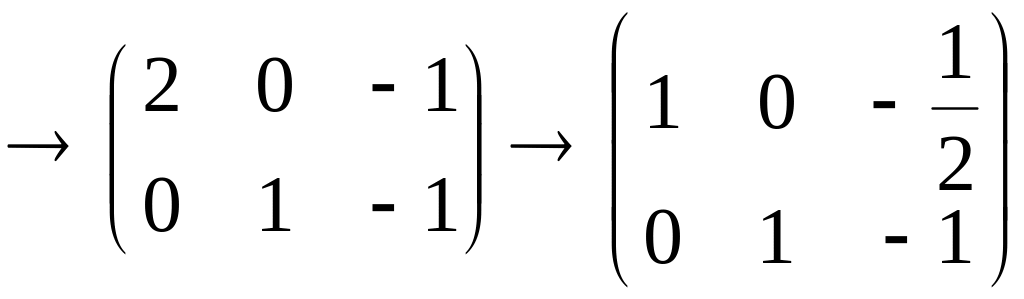и, следовательно, 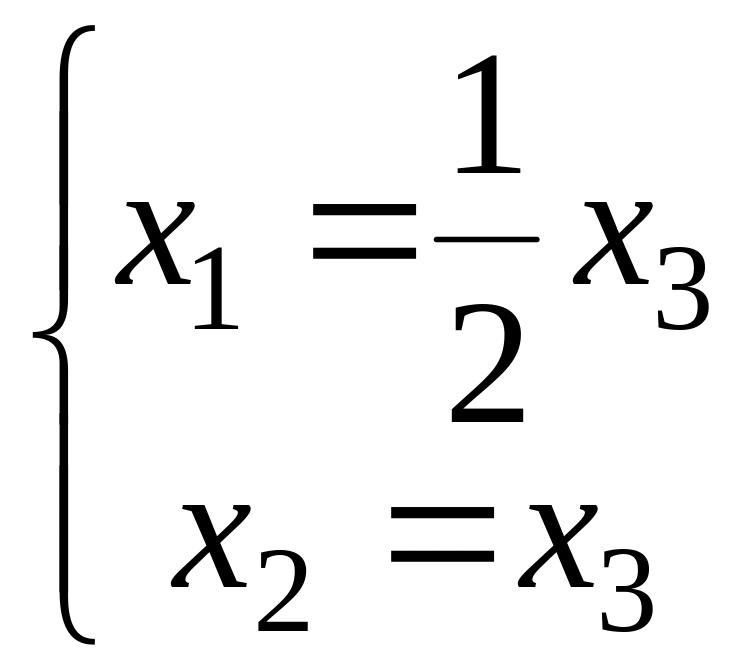, поэтому можем взять .

Векторы образуют жорданов базис матрицы.

Пример 4. Найти жорданову форму и жорданов базис матрицы оператора

.

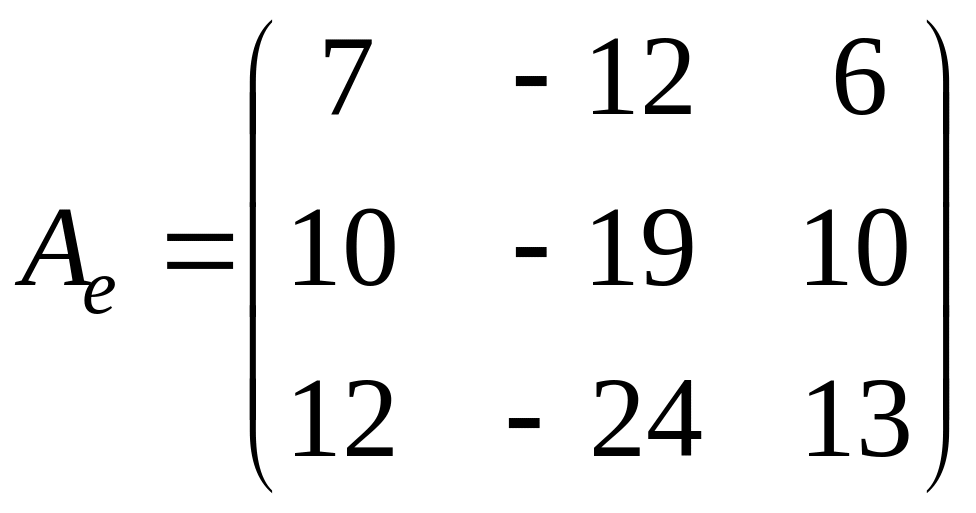Р е ш е н и е.

Вычислим

.

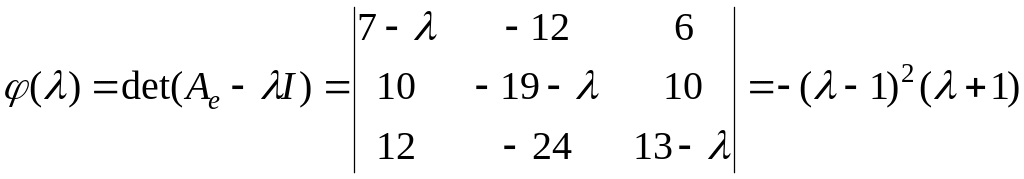Таким образом, получили два собственных значения , . Так как алгебраическая кратность равна 2, нужно вычислить геометрическую кратность собственного значения . Для этого посчитаем ранг матрицы

.

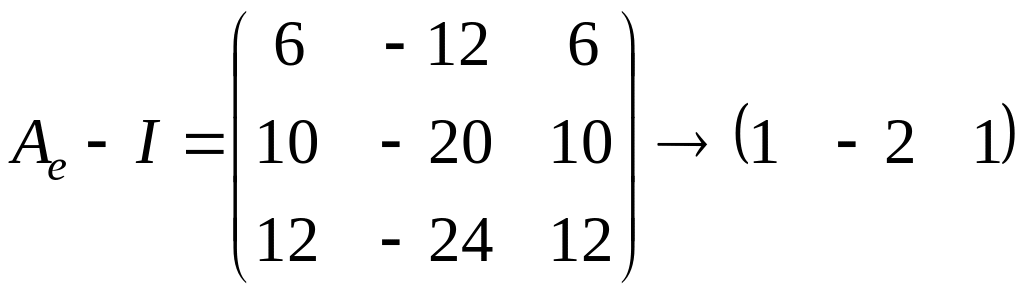Очевидно, что , поэтому и, следовательно, жорданова форма имеет следующий вид

.

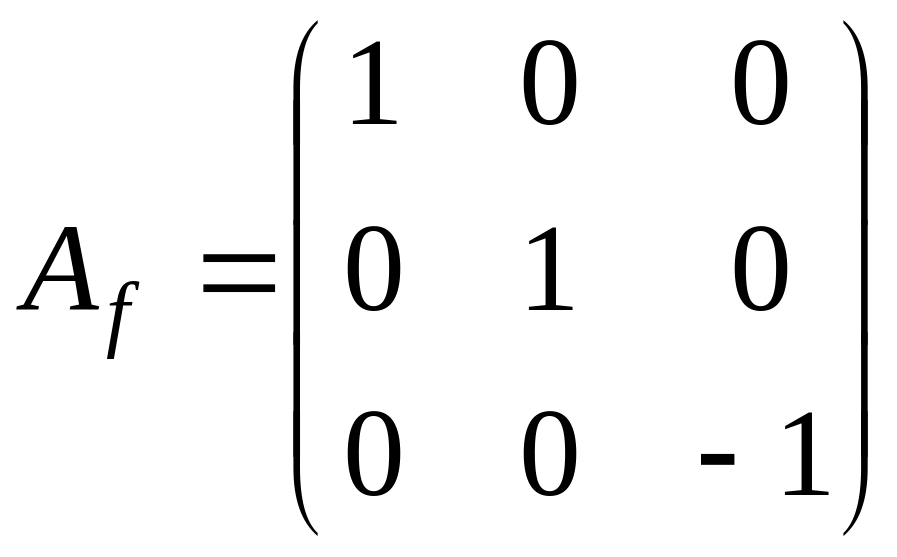Найдем собственные векторы , , соответствующие собственному значению . Очевидно, что они являются решением уравнения , а их координаты – решением системы

,

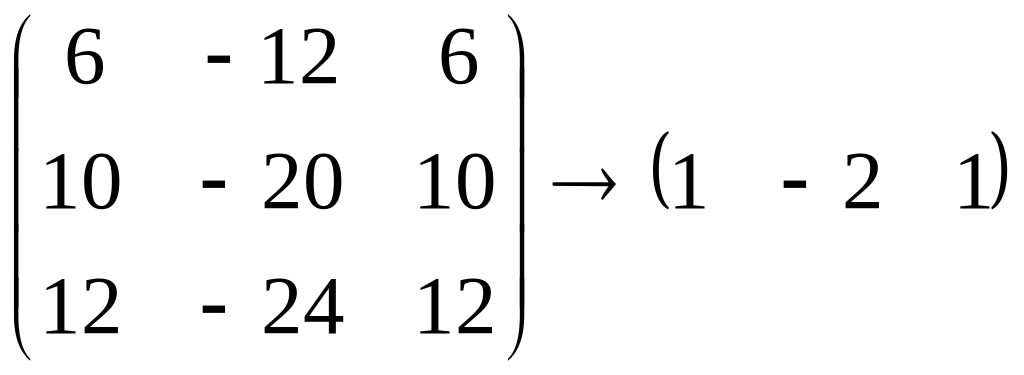и, следовательно, удовлетворяют уравнению

или .

Для нахождения ФСР построим таблицу

.

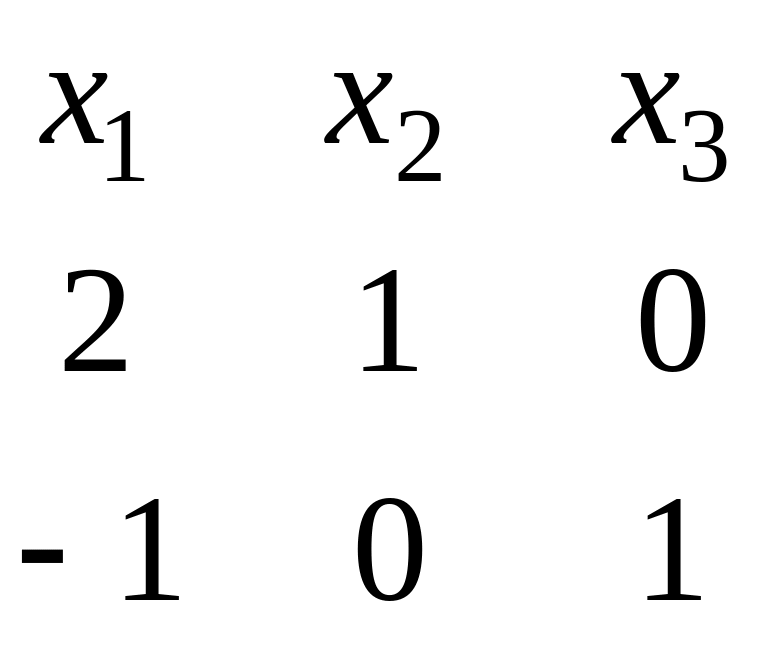Векторы , образуют фундаментальную систему решений в собственном подпространстве , поэтому любой собственный вектор, отвечающий собственному значению , линейно через них выражается и, следовательно, имеет вид

.

Так как , то нужно выбрать любые два линейно независимых вектора из этой линейной комбинации. Возьмем , .

Найдем собственный вектор , соответствующий собственному значению . Очевидно, что он удовлетворяет уравнению , а его координаты – системе

,

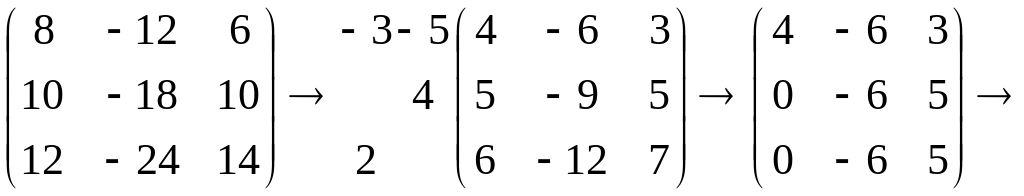
то ес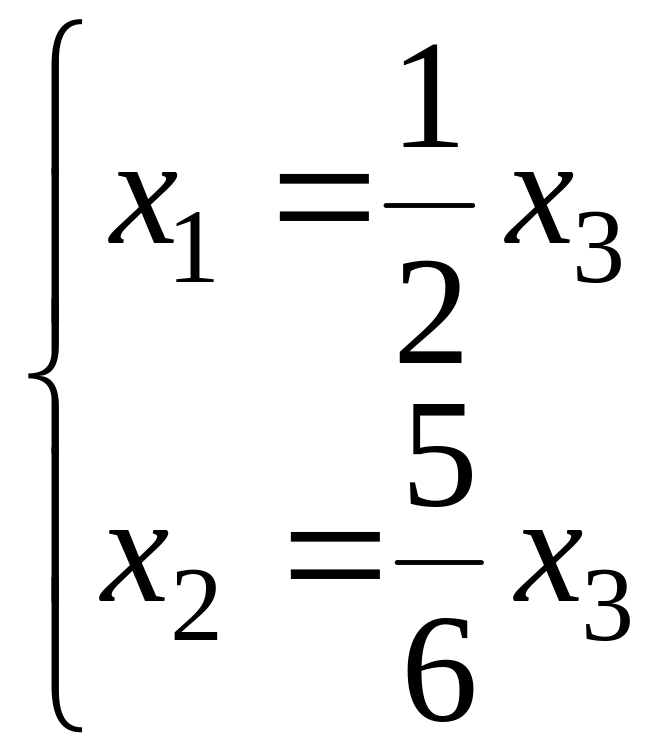ть , поэтому можем взять .

Векторы образуют жорданов базис матрицы.