
- •Руководство к решению задач по алгебре
- •Часть II Жорданова форма матрицы и жорданов базис
- •§1. Собственные векторы и собственные значения оператора.
- •Рассмотрим линейный оператор в пространстве и пусть – матрица этого оператора в некотором базисе .
- •1.2. Алгебраическая и геометрическая кратности собственного значения
- •Жорданова форма матрицы и жорданов базис
- •Алгоритм нахождения жорданова базиса для одной жордановой клетки
- •Алгоритм нахождения жордановой формы и жорданова базиса для матрицы 3-го порядка
- •1.5. Функции от матриц
- •§ 2. Жорданова форма матрицы
- •Оператор простой структуры
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Руководство к решению задач по алгебре
Часть II Жорданова форма матрицы и жорданов базис
Практическое пособие по курсу “Алгебра и геометрия”
для студентов по специальности
Воронеж
2003
§1. Собственные векторы и собственные значения оператора.
Жорданова форма матрицы и жорданов базис
Рассмотрим линейный оператор в пространстве и пусть – матрица этого оператора в некотором базисе .
Определение
1.
![]() называется характеристическим
многочленом
матрицы
называется характеристическим
многочленом
матрицы
![]() (
(![]() –
единичная матрица порядка
–
единичная матрица порядка
![]() ).
).
Определение
2. Вектор
![]() называется собственным вектором
оператора
,
если
называется собственным вектором
оператора
,
если
![]() ,
а
,
а
![]() – собственным значением оператора
,
соответствующим собственному вектору
– собственным значением оператора
,
соответствующим собственному вектору
![]() .
.
Алгоритм
 нахождения собственного значения и
собственного вектора оператора
нахождения собственного значения и
собственного вектора оператора
1)
Найдем все корни характеристического
многочлена
![]() ,
получим
,
получим
![]() – спектр оператора (множество всех
собственных значений);
– спектр оператора (множество всех
собственных значений);
2)
подставим
![]() в систему
в систему
![]() ,
,
решим
ее и найдем все собственные векторы,
отвечающие собственному значению
![]() ,
затем подставим
,
затем подставим
![]() и т.д.
и т.д.
1.2. Алгебраическая и геометрическая кратности собственного значения
Определение
3. Кратность
корня
![]() в характеристическом многочлене
в характеристическом многочлене
![]() называется алгебраической
кратностью собственного значения
.
называется алгебраической
кратностью собственного значения
.
Определение
4. Геометрической
кратностью
![]() собственного значения
называется размерность собственного
подпространства оператора
собственного значения
называется размерность собственного
подпространства оператора
![]() .
.
Утверждение.
![]() ,
где
– порядок матрицы оператора
.
,
где
– порядок матрицы оператора
.
Теорема.
Оператор
в базисе
![]() имеет диагональную матрицу
в том и только том случае, когда базисные
векторы
имеет диагональную матрицу
в том и только том случае, когда базисные
векторы
![]()
![]() – собственные, то есть
– собственные, то есть
![]() для всех
для всех
![]() .
.
Жорданова форма матрицы и жорданов базис
Определение 5. Жордановой клеткой называется клетка вида
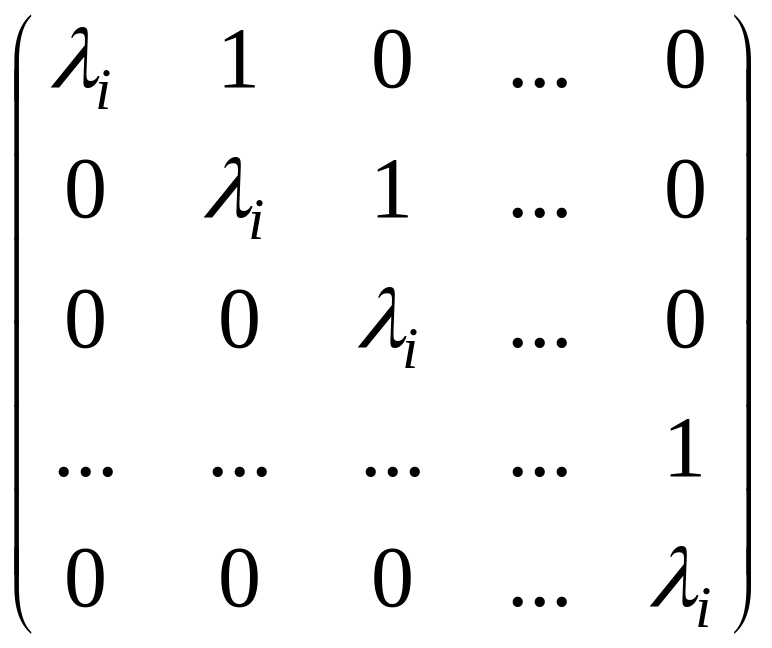 .
(1.1)
.
(1.1)
Теорема.
Для произвольного оператора
![]() существует базис пространства
существует базис пространства
![]() ,
в котором матрица оператора имеет
клеточно-диагональный вид, причем на
главной диагонали стоят жордановы
клетки вида (1.1).
,
в котором матрица оператора имеет
клеточно-диагональный вид, причем на
главной диагонали стоят жордановы
клетки вида (1.1).
Этот базис называется жордановым, а данный канонический вид матрицы называется жордановой формой.
Замечание. Жорданова форма определяется однозначно с точностью до порядка клеток (каждой клетке с соответствует один собственный вектор).
Алгоритм нахождения жорданова базиса для одной жордановой клетки
Рассмотрим
жорданову клетку вида (1.1). По определению
матрицы оператора в 1-м столбце стоит
вектор
![]() ,
разложенный по базису
,
разложенный по базису
![]() :
:
![]() ,
,
поэтому
![]() .
.
Во
2-м столбце матрицы находится вектор
![]() ,
разложенный по этому же базису и т.д.
,
разложенный по этому же базису и т.д.
Таким
образом, собственный вектор
![]() находим как решение системы
находим как решение системы
![]() ,
присоединенный вектор
,
присоединенный вектор
![]() – как решение системы
– как решение системы
![]() .
Очевидно, что
.
Очевидно, что
![]() .
.
Продолжая
аналогичные рассуждения, для вектора
![]() получим
получим
![]() .
.
Определение
6. Вектор
называется присоединенным
вектором высоты
![]() .
.
Жорданов базис состоит из собственных и присоединенных к ним векторов.
Утверждение. Алгебраическая кратность собственного значения равна сумме размеров жордановых клеток с этим собственным значением.
Утверждение. Геометрическая кратность собственного значения равна числу клеток в жордановой форме с собственным значением или числу линейно независимых собственных векторов, соответствующих собственному значению .
