3. Алгоритм распараллеливания.

Воспользуемся функциональным и геометрическим видом параллелизма. Пусть последний процесс будет выделен только лишь для анализа достижения точности вычислений. На все остальные процессы наложим исследуемую область. На эти процессы будут наложены полосы исследуемой области. На первой итерации определим значения на границах области и во внутренних точках области. Определим значение искомой функции, используя линейную интерполяцию и учитывая введённые столбцы дополнительных точек. Организуем итерационный процесс на каждом шаге, которого будут выполняться:

1. Все процессы кроме последнего процесса высчитывают значение искомой функции в своих внутренних точках и сразу же определяют, достигнута ли необходимая точность

do { pr=1;

for (int, j=1; j<m-1;j++)

for (int i=10; i<n-1;i++){

pn =u[i][j];

u[i][j]=0.25*(ω[i][j]+u[i+1][j]+u[i-1][j]+u[i][j-1]+u[i][j+1]);

if (fabs (pn – u[i][j])>ε)

pr=0;

}

2. Вычисляем новые значения на границах области;

3. Значения в граничных точках своих подобластей процессы получают от соседних процессов, для которых эти точки – внутренние. Передачу осуществляют за четыре такта. В данном случае передаём столбцы значений

4. Сапсапаритмспаимспи

4. Все процессы проверяют условие окончания итерационного процесса

Все процессы пересылают на последний процесс свой признак. Он анализирует полученные значения и если хотя бы один полученный признак <> 1 пересылает всем процессам значения признака = 0.

if (rank == size -1) {

int ind = 1;

for (i=0; i<size-1; i++) {

MPI_Recv (& ind, 1, MPI_INT,i,msgtag, MPI_COMM_WORLD,& Status);

if (ind ==0) pr=0

}

for (i=0;i<size-1;i++)

MPI_Send (& pr,1, MPI_INT,i, msgtag, MPI_COMM_WORLD);

}

else {

MPI_Send (& pr,1, MPI_INT,size-1, msgtag, MPI_COMM_WORLD);

MPI_Recv (& pr, 1, MPI_INT,size-1,msgtag, MPI_COMM_WORLD,& Status);

}

5. Все процессы последовательно печатают значения искомой функции , используя сквозную нумерацию элементов массива.

4. Ускорение вычислений

Ускорение достигается за счёт одновременного вычисления всеми процессами исходной функции во внутренних точках свих подобластей. Потеря времени за счёт передач. Потери точности при наложении на две точки не происходит.

Оптимизация на мвс

1. Постановка задачи. Пусть дана целевая функция f(x)→min, где x=(x₁,x₂....x_n) xєRⁿ

Необходимо найти :

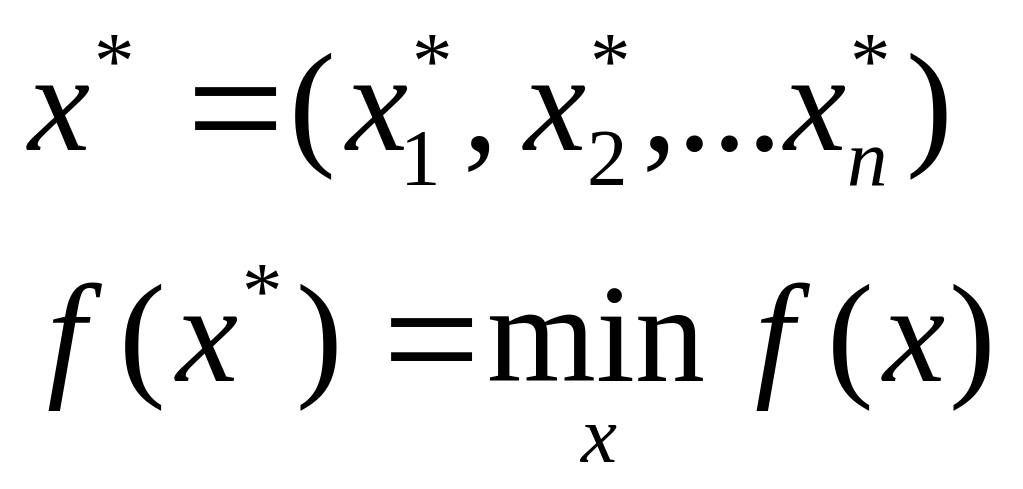
2. Расчётные формулы

Воспользуемся методом градиентного спуска. Определим начальную точку

x^k+1=x^k-h*gradf(x^e)

h – шаг спуска (длина шага метода)

Частные производные будем искать разностным способом, т.е.

- величина достаточно малая для точного вычисления производной

Останов итерационного процесса происходит:

• По числу шагов;

• При выполнении условия , ε – заданная точность.

3. Алгоритм распараллеливания

Воспользуемся функциональным видом параллелизма. Число используемых процессов size n+1, где n-размерность вектора x. Вначале все процессы знают вектор x₀. на каждой итерации будет выполняться следующее:

Действие Rank	1	2	3	4	5	6	7	8	9	10
0						xk+1 □□□□ Σ	pr	xk+1 pr	pr?
1	f(xk)								pr?
2	f(xk)								pr?
…	…	…	…	…	…	…	…	…	…	…
Size -1	f(xk)								pr?