
- •Лабораторная работа №20 измерение коэффициентов светопропускания, отражения, яркости и блеска различных материалов
- •Теоретическое обоснование
- •Описание установки
- •Выполнение работы
- •Упражнение I Измерение коэффициентов пропускания образцов
- •Упражнение II Измерение коэффициентов отражения и яркости
- •Упражнение III Измерение блеска
- •Контрольные вопросы
Лабораторная работа №20 измерение коэффициентов светопропускания, отражения, яркости и блеска различных материалов
Цель работы: ознакомиться с принципом работы фотоэлектрических приборов и научиться определять коэффициенты пропускания, отражения, яркости и блеска различных материалов.
Приборы и принадлежности: фотометр ФМ-58, источник питания, набор образцов, набор приспособлений.
Теоретическое обоснование
При падении световой волны на границу раздела двух прозрачных сред часть света отражается, часть проходит во вторую среду, а часть поглощается. Явления отражения, поглощения и пропускания света характеризуются с помощью соответствующих коэффициентов.
Коэффициенты отражения
![]() ,
поглощения
,
поглощения
![]() и пропускания
и пропускания
![]() определяются как отношения интенсивностей
соответственно отраженного JR,
поглощенного Jk,
прошедшего Jt
света к
интенсивности падающего света J0,
то есть
определяются как отношения интенсивностей
соответственно отраженного JR,
поглощенного Jk,
прошедшего Jt
света к
интенсивности падающего света J0,
то есть
![]() ;
;
![]() ;
;
![]() (20.1)
(20.1)
На основании закона сохранения энергии можно записать
![]() (20.2)
(20.2)
Решая совместно уравнения (20.1) и (20.2), получим
![]() (20.3)
(20.3)
то есть сумма коэффициентов отражения, поглощения и пропускания равна 1.
Если поглощение мало,
то k
можно принять равным 0, тогда
![]() .
Наоборот, если тело непрозрачно, то t=0
и тогда
.
Наоборот, если тело непрозрачно, то t=0
и тогда
![]()
Идеально белым телом
называется такое тело, у которого
коэффициент отражения R
равен 1. Поэтому R
характеризует степень белизны, а величина
![]() характеризует степень черноты тела.
характеризует степень черноты тела.
Френель предложил
естественную световую волну разложить
на две составляющие: Р и S,
у которых вектор напряженности
электрического поля
![]() совершает колебания соответственно в
плоскости падения волны Р, и в плоскости,
перпендикулярной к плоскости падения
волны S.
Применяя граничные условия (равенство
тангенциальных составляющих вектора
для падающей, отраженной и преломленной
волны) к волне, падающей на границу
раздела двух прозрачных сред, он вычислил
значение вектора
для Р и S
составляющих отраженных и преломленных
волн:
совершает колебания соответственно в
плоскости падения волны Р, и в плоскости,
перпендикулярной к плоскости падения
волны S.
Применяя граничные условия (равенство
тангенциальных составляющих вектора
для падающей, отраженной и преломленной
волны) к волне, падающей на границу
раздела двух прозрачных сред, он вычислил
значение вектора
для Р и S
составляющих отраженных и преломленных
волн:
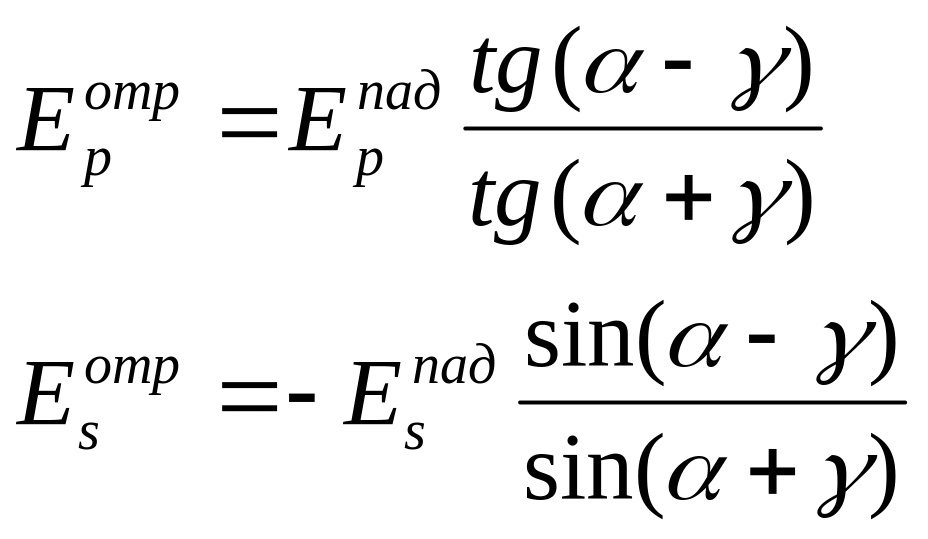
(20.4)
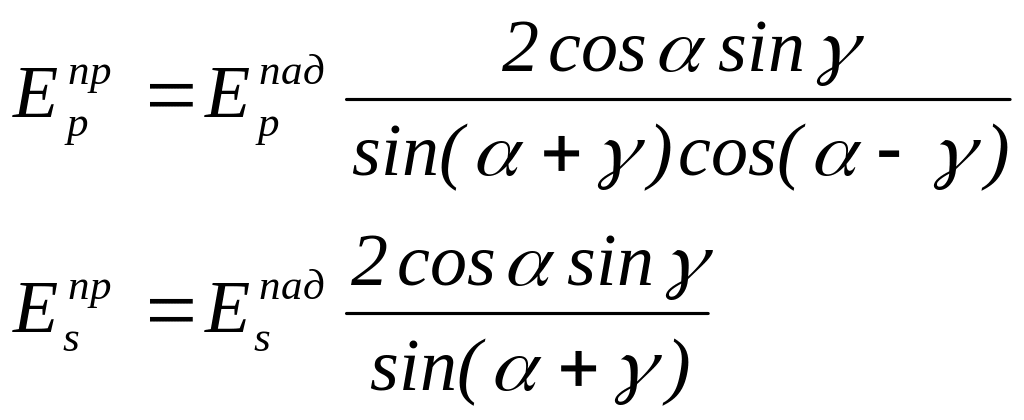
где
![]() – угол падения, γ – угол преломления,
– угол падения, γ – угол преломления,
![]() ,
,
![]() – амплитудное значение Р и S
составляющих вектора
падающей волны.
– амплитудное значение Р и S
составляющих вектора
падающей волны.
Формулы (20.4) получили название формул Френеля. Учитывая, что интенсивность света равна
![]() (20.5)
(20.5)
можно,
используя выражение (20.4), найти
интенсивность отражённой
![]() и преломленной
и преломленной
![]() волн через соответствующие коэффициенты
R
и T.
волн через соответствующие коэффициенты
R
и T.
Коэффициент отражения неразрывно связан с коэффициентом яркости В. Коэффициентом яркости поверхности называют отношение яркости светорассеивающей поверхности к яркости «идеального рассеивателя», находящегося в тех же условиях освещения.
За «идеальный рассеиватель» принимают поверхность, отражающую весь падающий на неё световой поток. В качестве такого «идеального рассеивателя» обычно берут баритовую пластинку. Близок к ней по отражению лист ватмановской бумаги.
В том случае, когда измеряемый образец и баритовая пластинка имеют одинаковые рассеивающие свойства, коэффициент отражения образца определяется из выражения
![]() (20.6)
(20.6)
где R – коэффициент отражения образца, В – отношение коэффициента яркости образца к яркости баритовой пластинки, Rn – коэффициент отражения баритовой пластинки.
Блеск испытуемой
поверхности характеризуется коэффициентом
![]() ,
который равен отношению коэффициентов
яркости образца при углах
и 00 ,
то есть
,
который равен отношению коэффициентов
яркости образца при углах
и 00 ,
то есть
![]() (20.7)
(20.7)
где
![]() – коэффициент яркости образца при
наклоне на угол
;
В0 –
коэффициент яркости образца при угле
00;
Р – поправка, учитывающая изменение
яркости испытуемого образца, происходящее
при углах от 00
до 450
,
– коэффициент яркости образца при
наклоне на угол
;
В0 –
коэффициент яркости образца при угле
00;
Р – поправка, учитывающая изменение
яркости испытуемого образца, происходящее
при углах от 00
до 450
,
![]() (20.8)
(20.8)
При работе на фотометрах отношение коэффициентов яркости образца при углах и 00 можно связать с отсчётами по правому барабану прибора при углах и 00.
Тогда формула (20.7) примет вид:
![]() (20.9)
(20.9)
где
100 – отсчёт по правому барабану при угле
00;
![]() - средний отсчёт по правому барабану
при угле наклона образца
.
- средний отсчёт по правому барабану
при угле наклона образца
.
