1. Обчислити визначники:

a)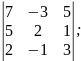 б)

2. Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:

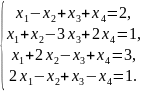
3. Обчислити значення матричного многочлена 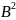+ 4(А-В) +AB -2E,якщо

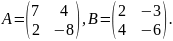
4. Знайти ранг матриці

5. Точки А(5; -3; 9), B(3;-15; 12), С(6; 5; 10) і S(2; -5; 7)- вершини пірамідиABCS.Знайти:

а) координати векторів , 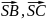та їхні довжини;

б) координати точки М перетину медіан трикутника ABC;

в) кути при вершиніSпірамідиABCS;

г) об'єм пірамідиABCS;

д) площу основиABC пірамідиABCS;

е) довжину висотиSO,проведеної з вершини S на основуABC.

6. Данотрикутник з вершинами A(-10;5),

В(14;-2) С(-4; 2)Знайти:

а)довжину сторони АВ;

б)рівняння прямої AM, яка паралельна стороні ВC;

в)рівняння висотиBF; '

г)рівняння медіаниAD;

д)внутрішній кут трикутника ;

е)координати точок N і К, що ділять більшу сторону трикутника на три рівні частини;

є)площу трикутника ABC.

7. Дано дві вершини трикутника А(-4; 3) і 6(4; -1) і точка перетину висот М(3; 3). Знайти третю вершину С.

8. Нехай задано координати двох точок (1; -1; 1), М₂(2; -1;-3), рівняння двох площин : х-4у+3z-1= 0, П₂: Зх - у - 5z - 8 = 0 тарівняння прямих

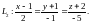
а)написати рівняння прямої, що проходить через точкиМ₁іМ₂, та знайти її напрямні косинуси;

б)знайти гострий кут між прямимиL₁іL₂;

в)через точку М₂ провести площину, паралельну площині П₂;

г)знайти гострий кут між площинами П₁ і П₂;

д)знайти відстань від точки M₁ до площини П₂;

е)через точку М₂ провести пряму паралельну прямійL₂;

є)знайти гострий кут між прямою L₂ і площиною П₂;

ж)через точкуM₁ провести пряму, перпендикулярну до площини П₁ і визначити напрямні косинуси цієї прямої;

з)написати рівняння площини, що проходить через точку М₁і перпендикулярну до площин П₁ і П₂;

и)написати рівняння прямої, яка задається як лінія перетину площин П₁ і П₂;

9. На еліпсі 9x²+ 25у² = 225 знайти точку, відстань від якої до правого фокуса в 4 рази більша відстані від неї до лівого фокуса.

10. Записати канонічне рівняння гіперболи, знаючи, що відстань від однієї з її вершин до фокусів дорівнює 9 і 1.

Варіант № 8

1. Обчислити визначники:

a)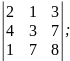 б)

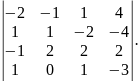
2. Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:

3. Обчислити значення матричного многочлена А² -5(А-Е)+ВА+ЗAB, якщо , .

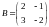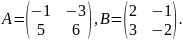
3. Знайти ранг матриці

4. Точки A(9; 6; 7), B(3; 6; -2), С(12; 2; 5) і S(8; 4; 2) — вершини пірамідиABCS. Знайти:

а)координати векторів , , та їхні довжини;

б)координати точки М перетину медіан трикутника ABC;

в)кути при вершиніSпірамідиABCS;

г)об'єм пірамідиABCS;

д)площу основиABC пірамідиABCS;

е)довжину висотиSO,проведеної з вершиниSна основуABC.

3. Дано трикутник з вершинами А(0; 7), В(6; -1), С(2; 1). Знайти:

а)довжину сторони АВ;

б)рівняння прямої AM, яка паралельна стороні ВС;

в)рівняння висотиBF;

г)рівняння медіаниAD,

д)внутрішній кут трикутника ;

е)координати точок N і К, що ділять більшу сторону трикутника на три рівні частини;

є)площу трикутникаABC.

7. Скласти рівняння множини точок площини, рівновіддалених від точкиF(0; 6) і від прямої у = 12. Знайти точки перетину цієї кривої з осями координат.

8. Нехай задано координати двох точок (4;0;-2), М₂(3; 4; -5),рівняння двох площин :8х+2у- -12= 0, П₂: 2х+у–z+2=0 та рівняння прямих :

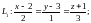
а)написати рівняння прямої, що проходить через точкиМ₁ і М₂, та знайти її напрямні косинуси;

б) знайти гострий кут між прямимиL₁іL₂;

в)через точку М₂ провести площину, паралельну площині П₂;

г)знайти гострий кут між площинами П₁ і П₂;

д)знайти відстань від точкиМ₁ до площини П₂;

е)через точку М₁ провести пряму, паралельну прямій L₂;

є)знайти гострий кут між прямою L₂ і площиною П₂;

ж) через точкуМ₁ провести пряму, перпендикулярну до площини П₁ і визначити напрямні косинуси цієї прямої;

з) написати рівняння площини, що проходить через точкуМ₁, і перпендикулярну до площин П₁ і П₂;

и) написати рівняння прямої, яка задається як лінія перетину площин П₁ і П₂.

8. Знайти кут між радіусами кола х²+у²+4х-6у= =0, проведеними в точки перетину з віссюОу.

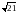
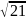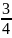9. Еліпс, симетричний відносно осей координат, фокуси якого знаходяться на осі Ох, проходить через точку М(-4; ) і має ексцентриситет . Записати рівняння еліпса.

Варіант № 9