
- •Розділ 3 індивідуальні домашні завдання
- •1. Обчислити визначники:
- •2. Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •4. Знайти ранг матриці
- •7. Нехай задано точки , площини та дві прямі
- •1. Обчислити визначники:
- •4. Знайти ранг матриці
- •6. У трикутнику з вершинами . Знайти:
- •1. Обчислити визначники:
- •4. Знайти ранг матриці
- •6. Дано трикутник з вершинами . Знайти:
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці .
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці .
- •1. Обчислити визначники:
- •2. Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці .
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •4. Знайти ранг матриці
- •Обчислити визначники:
- •Знайти ранг матриці
- •Обчислити визначники:
- •Знайти ранг матриці
- •Обчислити визначники:
- •Знайти ранг матриці .
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці
- •1. Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці .
- •1. Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці .
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •Знайти ранг матриці .
- •Обчислити визначники:
- •Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •4.Знайти ранг матриці .
- •2. Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •4. Знайти ранг матриці
- •6. Дано трикутник з вершинами . Знайти:
- •1. Обчислити визначники:
- •2. Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
- •4. Знайти ранг матриці
Розділ 3 індивідуальні домашні завдання
Варіант № 1
1. Обчислити визначники:
а)
 ;
б)
;
б)
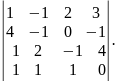
2. Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним
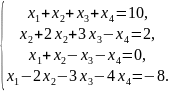
3.
Обчислити значення матричного многочлена
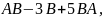 якщо
якщо
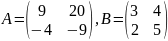 .
.
4.
Знайти ранг матриці
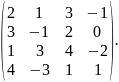
5.
Точки
 і
і
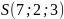 вершини піраміди
вершини піраміди
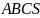 .
Знайти:
.
Знайти:
а)
координати векторів
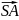 ,
,
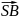 ,
,
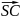 та
їхні довжини;
та
їхні довжини;
б) координати точки M перетину медіан трикутника ABC;
в) кути при вершині S піраміди ABCS;
г) об'єм піраміди ABCS;
д) площу основи ABC піраміди ABCS;
е) довжину висоти SO, проведеної з вершини S на основу ABC .
6.
У трикутнику з вершинами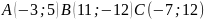 .
Знайти:
.
Знайти:
а) довжину сторони АВ;
б) рівняння прямої АМ,яка паралельна стороні ВС;
в) рівняння висоти BF;
г) рівняння медіани AD;
д)
внутрішній кут трикутника
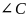 ;
;
е) координати точок Ni К, що ділять більшу сторону трикутника на три рівні частини;
є) площу трикутника ABC.
7.
Нехай задано точки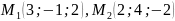 ,
площини
,
площини
 та
дві прямі
та
дві прямі
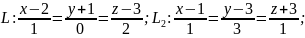
а)
написати рівняння прямої, що проходить
через точки
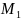 і
і
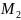 ,
та знайти її напрямні косинуси;
,
та знайти її напрямні косинуси;
б)
знайти гострий кут між прямими
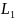 і
і
 ;
;
в)
через точку
провести площину, паралельну площині
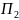 ;
;
г)
знайти гострий кут між площинами
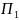 і
;
і
;
д) знайти відстань від точки до площини ;
е) через точку провести пряму, паралельну прямій ;
є) знайти гострий кут між прямою і площиною ;
ж) через точку провести пряму, перпендикулярну до площини і визначити напрямні косинуси цієї прямої;
з) написати рівняння площини, що проходить через точку і перпендикулярна до площин і ;
и)
написати рівняння прямої, яка задається
як лінія перетину площин
і
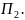
8.
Знайти канонічне рівняння прямої
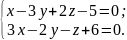
9.
Скласти рівняння гіперболи, фокуси якої
розміщені на осі абсцис симетрично
відносно початку координат, якщо велика
вісь еліпса дорівнює 16, а ексцентриситет
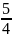 .
.
10.
Дана парабола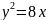 .
Записати рівняння хорди параболи,
.
Записати рівняння хорди параболи,
яка
в точці
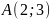 ділиться
навпіл. Визначити довжину хорди параболи,
яка проходить через фокус, перпендикулярно
до осі.
ділиться
навпіл. Визначити довжину хорди параболи,
яка проходить через фокус, перпендикулярно
до осі.
Варіант № 2
1. Обчислити визначники:
а)
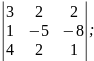 б)
б)
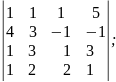
2. Розв'язати систему лінійних рівнянь, користуючись методами: Крамера, Гаусса та матричним:
3.
Обчислити значення матричного многочлена
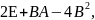
якщо
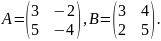
4. Знайти ранг матриці
5.
Точки
 —
вершини піраміди
.
Знайти:
—
вершини піраміди
.
Знайти:
а) координати векторів , , та їхні довжини;
б) координати точки M перетину медіан трикутника ABC;
в) кути при вершині S піраміди ABCS;
г) об'єм піраміди ABCS;
д) площу основи ABC піраміди ABCS;
е) довжину висоти SO, проведеної з вершини S на основу ABC
6.
Дано трикутник з вершинами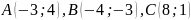 .
Знайти:
.
Знайти:
а) довжину сторони АВ;
б) рівняння прямої АМ,яка паралельна стороні ВС;
в) рівняння висоти BF;
г) рівняння медіани AD;
д) внутрішній кут трикутника ;
е) координати точок Ni К, що ділять більшу сторону трикутника на три рівні частини;
є) площу трикутника ABC.
7. Нехай задано точки , площини та дві прямі
а) написати рівняння прямої, що проходить через точки і , та знайти її напрямні косинуси;
б) знайти гострий кут між прямими і ;
в) через точку провести площину, паралельну площині ;
г) знайти гострий кут між площинами і ;
д) знайти відстань від точки до площини ;
е) через точку провести пряму, паралельну прямій ;
є) знайти гострий кут між прямою і площиною ;
ж) через точку провести пряму, перпендикулярну до площини і визначити напрямні косинуси цієї прямої;
з) написати рівняння площини, що проходить через точку і перпендикулярна до площин і ;
и) написати рівняння прямої, яка задається як лінія перетину площин і
8.
Записати рівняння кола, що має центр у
фокусі параболи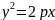 ,
яке дотикається до її директриси.
,
яке дотикається до її директриси.
9. Записати канонічне рівняння еліпса, знаючи, що відстань між фокусами дорівнює 8, а мала піввісь дорівнює 3. Знайти його ексцентриситет.
10.
Гіпербола, симетрична відносно осей
координат, проходить через точку
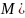 і
має уявну піввісь 2. Записати рівняння
гіперболи і знайти відстань від точки
Мдо фокусів.
і
має уявну піввісь 2. Записати рівняння
гіперболи і знайти відстань від точки
Мдо фокусів.
Варіант № 3
1. Обчислити визначники:
а)
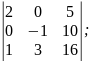 б)
б)
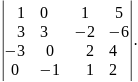
2.
Розв'язати систему лінійних рівнянь,
користуючись методами: Крамера,
Гаусса та
матричним: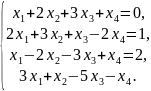
3.
Обчислити
значення
матричного
многочлена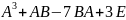 ,
якщо
,
якщо
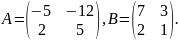
4.
Знайти ранг матриці
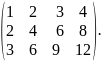
5.
Точки
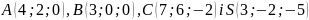 —
вершини піраміди
.
Знайти:
—
вершини піраміди
.
Знайти:
а) координати векторів , , та їхні довжини;
б) координати точки M перетину медіан трикутника ABC;
в) кути при вершині S піраміди ABCS;
г) об'єм піраміди ABCS;
д) площу основи ABC піраміди ABCS;
е) довжину висоти SO, проведеної з вершини S на основу ABC
6.
Дано трикутник з вершинами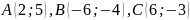 .
Знайти:
.
Знайти:
а) довжину сторони АВ;
б) рівняння прямої АМ,яка паралельна стороні ВС;
в) рівняння висоти BF;
г) рівняння медіани AD;
д) внутрішній кут трикутника ;
е) координати точок Ni К, що ділять більшу сторону трикутника на три рівні частини;
є) площу трикутника ABC.
7.
Нехай задано координати точок рівняння площин
рівняння площин
 та
два рівняння
прямих
та
два рівняння
прямих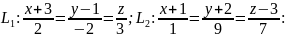
а) написати рівняння прямої, що проходить через точки і , та знайти її напрямні косинуси;
б) знайти гострий кут між прямими і ;
в) через точку провести площину, паралельну площині ;
г) знайти гострий кут між площинами і ;
д) знайти відстань від точки до площини ;
е) через точку провести пряму, паралельну прямій ;
є) знайти гострий кут між прямою і площиною ;
ж) через точку провести пряму, перпендикулярну до площини і визначити напрямні косинуси цієї прямої;
з) написати рівняння площини, що проходить через точку і перпендикулярна до площин і ;
и) написати рівняння прямої, яка задається як лінія перетину площин і
8.
Знайти довжину хорди еліпса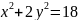 ,
що ділить кут між осями навпіл.
,
що ділить кут між осями навпіл.
9.
Написати рівняння параболи і її
директриси, якщо парабола проходить
через точки перетину прямої
 і
кола
і
кола
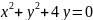 і
симетрична відносно осі
і
симетрична відносно осі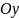 .
.
10. Записати рівняння гіперболи, що має вершини в фокусах а
фокуси
в вершинах еліпса
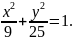
Варіант № 4
1. Обчислити визначники:
а)
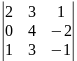 ;
б)
;
б) 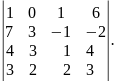
2.
Розв'язати систему лінійних рівнянь,
користуючись методами: Крамера,
Гаусса та
матричним: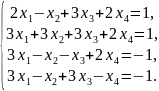
3.
Обчислити значення матричного
многочлена
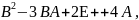 якщо
якщо
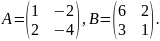
4.
Знайти ранг матриці
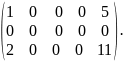
5.
Точки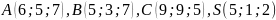 —
вершини піраміди
.
Знайти:
—
вершини піраміди
.
Знайти:
а) координати векторів , , та їхні довжини;
б) координати точки M перетину медіан трикутника ABC;
в) кути при вершині S піраміди ABCS;
г) об'єм піраміди ABCS;
д) площу основи ABC піраміди ABCS;
е) довжину висоти SO, проведеної з вершини S на основу ABC.
6.
У трикутнику з вершинами
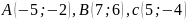 .
Знайти:
.
Знайти:
а) довжину сторони АВ;
б) рівняння прямої АМ,яка паралельна стороні ВС;
в) рівняння висоти BF;
г) рівняння медіани AD;
д) внутрішній кут трикутника ;
е) координати точок Ni К, що ділять більшу сторону трикутника на три рівні частини;
є) площу трикутника ABC.
7.
Нехай задано координати точок
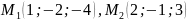 ,
рівняння площин
,
рівняння площин
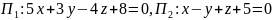 та
два рівняння
прямих
та
два рівняння
прямих
а) написати рівняння прямої, що проходить через точки і , та знайти її напрямні косинуси;
б) знайти гострий кут між прямими і ;
в) через точку провести площину, паралельну площині ;
г) знайти гострий кут між площинами і ;
д) знайти відстань від точки до площини ;
е) через точку провести пряму, паралельну прямій ;
є) знайти гострий кут між прямою і площиною ;
ж) через точку провести пряму, перпендикулярну до площини і визначити напрямні косинуси цієї прямої;
з) написати рівняння площини, що проходить через точку і перпендикулярна до площин і ;
и) написати рівняння прямої, яка задається як лінія перетину площин і
8.
Записати рівняння параболи, що має
ексцентриситет ,
проходить через точки (0; 0) і(1;-3) та
симетрична відносно осі
.
Знайти рівняння директриси.
,
проходить через точки (0; 0) і(1;-3) та
симетрична відносно осі
.
Знайти рівняння директриси.
9.
Записати рівняння гіперболи, що має
ексцентриситет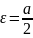 ,
,
проходить
через точку
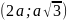 і
симетрична відносно осей координат.
і
симетрична відносно осей координат.
10.
Асимптота гіперболи
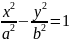 утворює
з віссю
утворює
з віссю
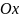 кут
60°.
кут
60°.
Записати
рівняння діаметра, спряженого з
діаметромy .
.
Варіант № 5
