120

Лабораторная работа №24 Исследование входных характеристик и трансформирующих свойств цепей с распределенными параметрами

1. Цель работы: изучить входные характеристики и трансформирующие свойства цепей с распределенными параметрами.

2. Теоретические положения

Входное сопротивление цепи с распределенными параметрами в некотором сечении линии можно рассчитать, поделив комплексное действующие значение напряжения на комплексное действующее значение тока в данном сечении. В общем случае для линии без потерь

Z_вх= ,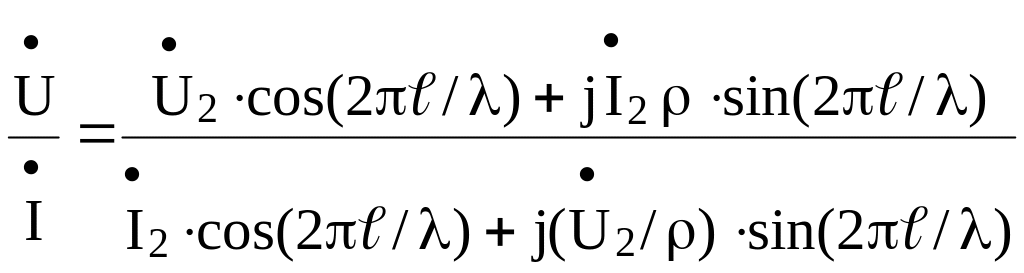

где ℓ/λ – электрическая длина линии.

В режиме холостого хода (I₂=0) Z_вх имеет чисто мнимый характер:

Z_вх.х= .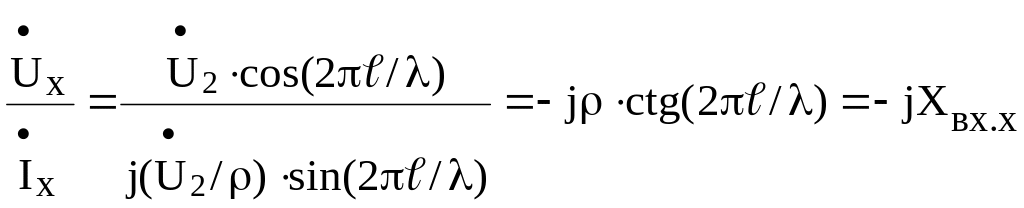

Напомним, что для линии без потерь Z_вх= – величина вещественная.

Тот факт, что Z_вх.х=jX чисто реактивное, означает, что в длинной линии без потерь мощность падающей волны нигде не расходуется и полностью возвращается к генератору в виде мощности отраженной волны, т.е. длинная линия обменивается реактивной мощностью с источником энергии.

Если ℓ/λ – целое число, то Z_вх может быть равно нулю или ±∞. В этих случаях в длинной линии наблюдается резонанс токов или напряжений.

Условия резонанса токов ℓ/λ=(1/4)(2к+1), к=0,1,2,3,…∞.

Условия резонанса напряжений ℓ/λ=к/2, к=1,2,3,…∞.

При ℓ=0 Z_вх=-j∞, при ℓ=λ/4 Z_вх=0; при ℓ=λ/2 Z_вх=j∞ и т.д. Зависимость X_вх.х от длины линии показаны на рис.1. Как видно из рисунка, входное сопротивление разомкнутой линии длиной менее четверти длины волны имеет емкостной характер, длиной от ¼ до ½ – индуктивный характер и т.д. Свойства разомкнутого отрезка линии длиной ¼ и ½ подобны свойствам последовательного и параллельного контуров.

Примечание: Разомкнутая линия с сосредоточенными параметрами в режиме х.х. может рассматриваться как совокупность двух обкладок конденсатора, обладающего емкостью С_л=С₀·ℓ.

В режиме короткого замыкания входное сопротивление линии имеет также чисто реактивный характер, причем знак Z_вх.к также меняется через четверть длины волны, так как “tg”– функция нечетная.

Z_вх.к= .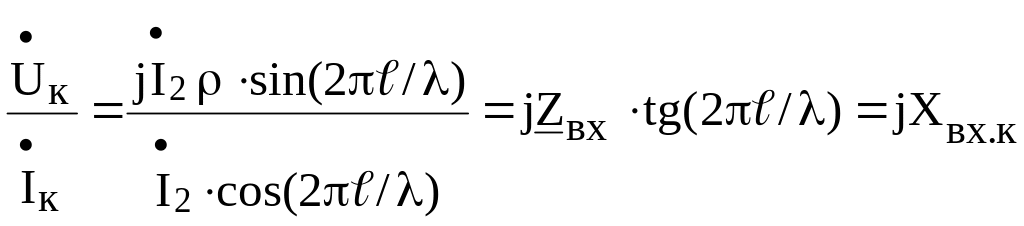

X_вх.х

ℓ λ 3λ/4 λ/2 λ/4

0

Рис.1

Зависимость X_вх.к. короткозамкнутой линии без потерь от электрической длины ℓ линии изображена на рис.2. Следует обратить внимание на то, что короткозамкнутая линия без потерь длиной в четверть длины волны имеет бесконечно большое входное сопротивление. Если в линии имеются потери, то входное сопротивление не бесконечно, но достаточно велико. Этим свойством короткозамкнутых четвертьволновых линий часто пользуются на практике. В

X_вх.х

ℓ λ 3λ/4 λ/2 λ/4

0

Рис.2

линии без потерь, нагруженной на несогласованную нагрузку (Z_н=R₂≠ρ);

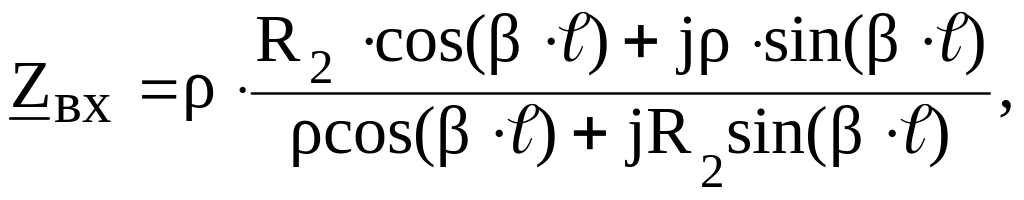
причем при R₂> ρ:

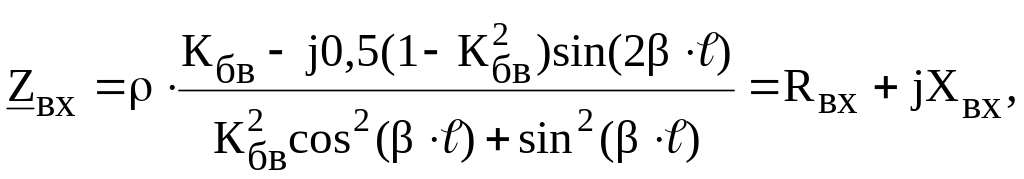
где

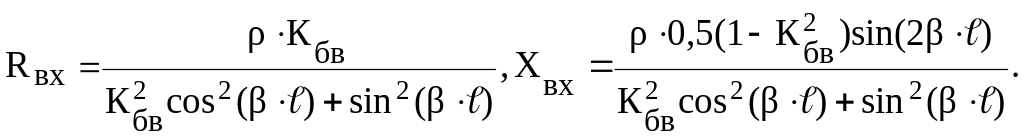
Из этих выражений следует, что входное сопротивление в любом сечении “ℓ” длинной линии имеет комплексный характер, за исключением тех сечений, где sin(2βℓ)=0. Называя эти сечения резонансными можем найти ℓ_рез=n·λ/ℓ, где n=0,1,2,… .

Следовательно, резонансные сечения повторяются через λ/4 считая от конца линии. В этих сечениях Z_вх имеет активный характер.

При 0<ℓ<λ/4, Z_вх=R-jX; ℓ_рез=λ/4, Z_вх= ρ /R₂.

При λ/4<ℓ<λ/2, Z_вх=R+jX; ℓ_рез=λ/2, Z_вх=R₂.

Рассматривая аналогично режим при R₂<ρ, можно найти ℓ_рез=n·λ/4, откуда:

при n=0, ℓ_рез=0, Z_вх=R₂;

при 0<ℓ<λ/4 “X” имеет индуктивный характер; ℓ_рез=λ/4, Z_вх= ρ²/R₂;

при λ/4 <ℓ<λ/2 “X” имеет емкостной характер; ℓ_рез=λ/2, Z_вх=R₂.

Следовательно, отрезок линии длиной λ/4 замкнутый на (R₂<ρ) является трансформатором сопротивления, повышающим “R₁” до величины ρ²/R₂>R₂.

Для получения наперед заданного сопротивления R₁>R₂ можно применить четвертьволновой трансформатор с .

При замыкании линии на элемент с чисто реактивным сопротивлением входное сопротивление будет иметь вид:

• длинная линия замкнута на емкость

Z_вх=jρ·ctg[β(ℓ+ℓ`)], где ℓ`= < λ/4;

• длинная линия замкнута на индуктивность

Z_вх=jρ·tg[β(ℓ+ℓ`)], где ℓ`= < λ/4.

В линии без потерь, нагруженный на резистор, сопротивление которого равно волновому, ,

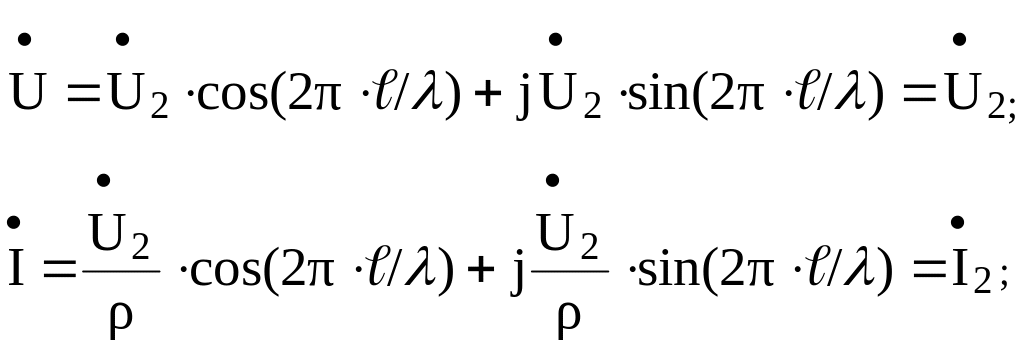
Z_вх= .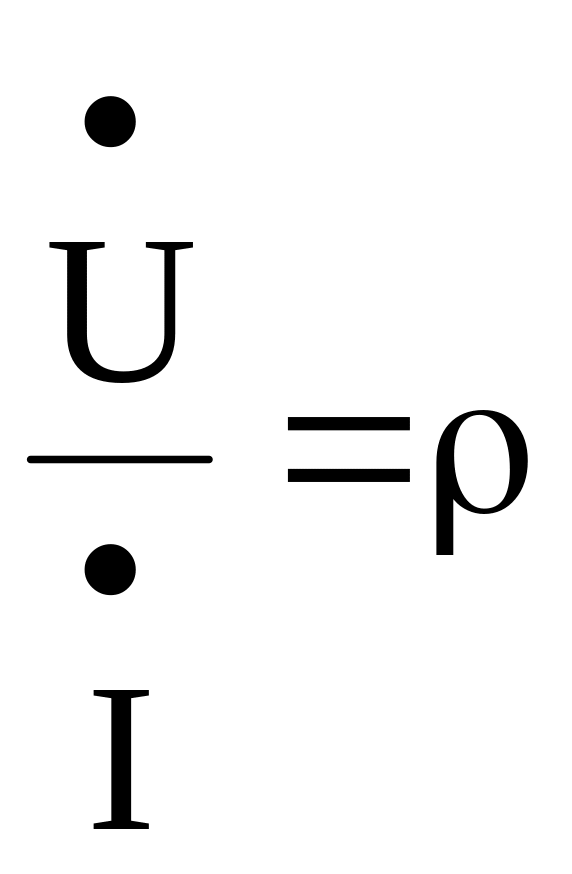

Таким образом, при согласованной нагрузке напряжения на любом расстоянии от конца линии равно напряжению, подведенному от генератора, ток , а входное сопротивление линии в любом сечении равно волновому: Z_вх= ρ (см. рис.5).

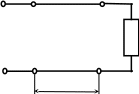
Рассмотрим входное сопротивление отрезка линии без потерь длиной λ/4, нагруженного на резистор Z_н=R_н (рис.3). Если в выражениях для и ℓ=λ/4,

то:

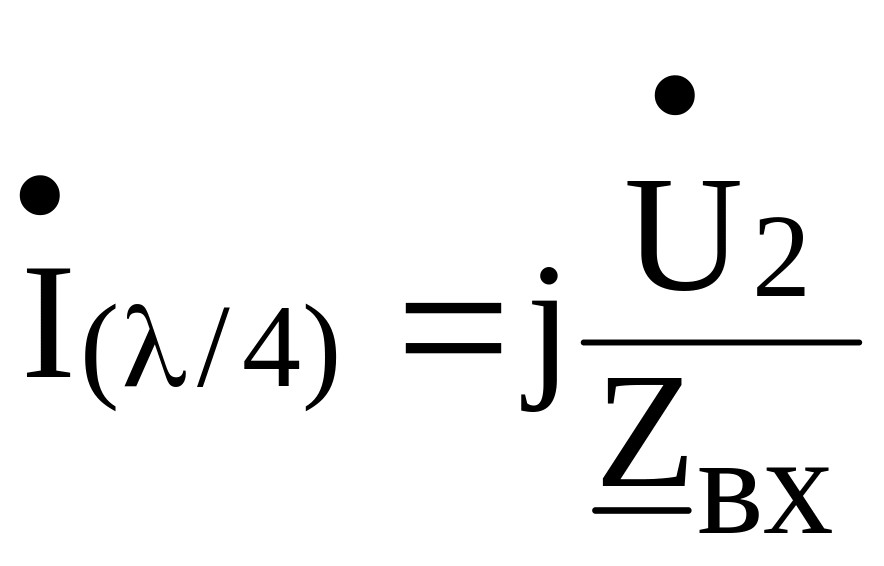
A D

Z _вх(λ/4) ρ Z_н ρ₁ ρ₂ Z_н= ρ₂

ℓ=λ/4 B ℓ= λ/4 F

Рис.3 Рис.4

При этом входное сопротивление линии

.

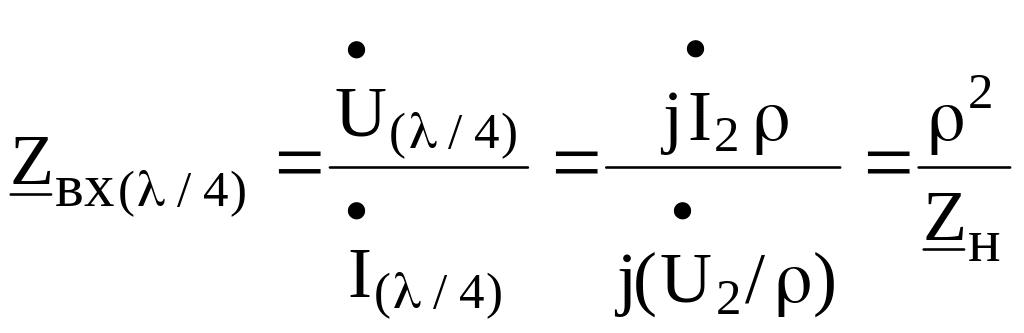Следовательно, входное сопротивление четвертьволновой линии обратно пропорционально сопротивлению нагрузки Z_н. Этим свойством четвертьволновых линий широко пользуются для практических целей, например, для согласования линии с нагрузкой или для согласования линий с различными волновыми сопротивлениями. Пусть волновое сопротивление первой линии ρ₁, второй – ρ₂. Чтобы выход первой линии соединить с входом второй, необходимо между этими линиями поставить согласующий трансформатор в виде четверть волнового отрезка линии с волновым сопротивлением (рис.4). Для ρ₁=100 Ом; ρ₂=400 Ом волновое сопротивление согласующей линии =200 Ом. Тогда выход первой линии будет нагружен на R=200²/400=100 Ом, а вход второй линии подключен к R=200²/100=400 Ом (рис.5).

A D A D

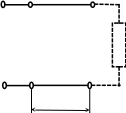
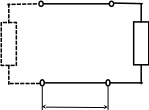
ρ₁=100 Ом Z_н1=400 Oм Z_н1=100 Oм

Z_вх=400 Ом Z_н2=400 Oм

ρ_согл=200 Ом ρ_согл=200 Ом

B ℓ=λ/4 F B ℓ=λ/4 F

Рис.5

Таким образом, если первая линия не имеет согласующего трансформатора, то для получения согласованного режима ее следует нагрузить на резистор с сопротивлением 100 Ом. Если к концу линии подключить четвертьволновый отрезок с волновым сопротивлением 200 Ом, то для согласной работы первой линии к выходным точкам согласующей линии ( к точкам D, F на рис.4) нужно подключить не 100, а 400 Ом. Аналогично, для согласованной работы второй линии к ее выходу необходимо подключить без какого-либо согласующего устройства источник сопротивлением 100 или 400 Ом, включенный через согласующую линию.