16.3Методичні вказівки до виконання роботи.

16.3.1Постановка задачі.

В першу чергу необхідно вивести рівняння, коренем якого і буде шукане значення напруги, і звести це рівняння до вигляду (1). За законом Ома отримаємо:

I=(EU_Н)R.^ (8)

Крім того, відома залежність струму від напруги на НД:

I=f(U_Н). (9)

При виконанні роботи необхідно подати суміщені графіки функцій (8) і (9) в осях І, U_Н (так званий графічний розв’язок). На Рис. 16 .2 наведений приклад графічного розв’язку для схеми Рис. 16 .1, НД – діод Д226Б, R=2 Ом.

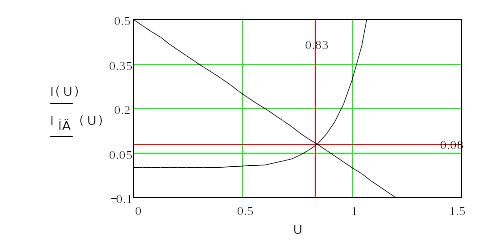
Рис. 16.2. Приклад графічного розв’язку рівняння.

Виключаючи струм І з рівнянь (8) і (9) отримаємо:

F(U_H)=f(U_Н)(EU_Н)R=0. (10)

З фізичних міркувань очевидно, що значення U_Н не може бути від’ємним і не може перевищувати е.р.с. Е. Oтже, інтервал локалізації відомий: U_Н  [0,E] (більш точно можна визначити за допомогою графічного розв’язку). При використанні методів хорд та дотичних необхідно вивести ітераційні формули, а для методу порозрядного наближення  задати початковий крок та коефіцієнт розрядності.

Вхідними даними програми є: е.р.с. джерела, опір резистора та припустима похибка визначення напруги, а також значення констант, які входять в вираз (9). Вихідні дані  значення напруги на НД та струму в колі. При виведенні вихідних даних на екран необхідно вказати їх розмірність.

16.3.2Розробка структури даних.

Крім вхідних та вихідних змінних необхідно впровадити змінні для реалізації методу розв’язку, наприклад, наступне наближення кореня, ітераційне прирощення, значення функцій F(x), крок та коефіцієнт розрядності, поточні границі інтервалу локалізації.

Додатково необхідно також передбачити змінні для зберігання констант, які входять в нелінійну залежність I(U_Н), що полегшує модифікацію нелінійних функцій при тестуванні програми.

16.3.3Розробка алгоритму.

Оскількі ітераційні наближення до кореня повторюються невизначену наперед кількість разів, основою алгоритму є цикли “поки” або “до”. Для першого умовою закінчення є критерій (3) при =R, а для другого  критерій (2) при .

Контроль зміни знаку функції F(x) доцільно здійснювати порівнюючи з нулем добуток F(x_n)F(x_n+1), який буде від’ємним лише при різних знаках множників.

В алгоритм необхідно включити перевірку заданого інтервалу локалізації на наявність кореня (якщо F(a)F(b)>0, то кількість коренів на інтервалі парна, або корені відсутні) із відповідними повідомленням. Доцільно також підрахувати кількість ітерацій і припиняти роботу програми при перевищенні цією кількістю великого, наперед заданого розробником, числа (захист від зациклювання).

На блок-схемі алгоритму необхідно відмітити контрольні точки, зручні для спостереження за збіжністю ітерацій.

16.3.4Написання тексту програми.

Для полегшення налагодження програми доцільно задавати значення вхідних змінних операторами вводу раніш підготованих данних або присвоєнням. Розрахунок значень нелінійних функцій та розрахунки за ітераційними формулами оформлюються у вигляді підпрограм. Приклад тексту програми, котра реалізує розв’язок нелінійного рівняння методом порозрядного наближення:

program lab16P;

uses crt;

const

E =5;

R =200;

eps =0.000001;

c:real =E/10;

u:real =0;

function SumU(U:real):real;

begin

SumU:=0.0001*(EXP(8*U)-1)-(E-U)/R;

end;

begin

ClrScr;

while ABS(SumU(u))>eps do

begin

if SumU(u)*SumU(u+c)<0 then begin

u:=u+c;

c:=-c/10

end;

u:=u+c;

writeln(‘U=’,u);

end;

writeln(‘I=’,(E-U)/R)

end.

16.3.5Налагодження і тестування.

В результатах тестування програми необхідно навести значення всіх наближень до кореня, вказати кількість необхідних ітерацій. Повторити розрахунки при зменшеному значені похибки  і зробити висновки про швидкість збіжності ітераційного процесу. Навести результати розв’язку рівняння при змінених значеннях будь-якого електричного параметра схеми.

17.Лабораторна робота №17

Числове розв’язування диференційних рівнянь

Мета робoти – засвоїти основні числові методи розв’язування диференційних рівнянь, а також виробити навики програмної реалізації цих методів.

17.1Теоретична частина.

Диференційне рівняння  це рівняння, яке зв’язує дві чи більше функціонально залежні одна від одної величини та їх похідні.

17.1.1Деякі методи числового розв’язування диференційних рівнянь.

Розв’язування диференційного рівняння вигляду

dx(t)dt=F(x,t) (1)

полягає у знаходженні такої функції x(t), похідна якої задовільняла би тотожності (1), причому сама функція при заданому значенні аргументу t_o приймає початкове значення x_o (задача Коші):

x(t_o)=x_o. (2)

Якщо функція F(x,t) не містить явної залежності від аргументу t, тобто F(x,t)=F(x), то рівняння (1) називається автономним. У разі, коли інтеграл F(x,t)dt може бути виражений через елементарні функції, задача Коші розв’язується аналітично і числові методи зводяться до табулювання або графічного відображення відомої функції x(t). Але аналітичний розв’язок задачі Коші неможливий у багатьох практично важливих випадках, коли F(x,t) містить нелінійні (зокрема трансцендентні) функції та їх комбінації. У цьому випадку застосовується наближене числове інтегрування рівняння (1), яке полягає у такому:

1. Вибирають крок h зміни незалежної змінної t. Це дозволяє перейти від розгляду неперервої функції x(t) до розгдяду дискретної послідовності значень цієї функції x_i. Крок h може бути змінним.

2. Вибирають рекурентну формулу, за якою розраховують наступне значення функції x_i+1 через відоме попереднє x_i+1=f(x_i,t_i). Методи числового розв’язування диференційних рівнянь відрізняються виглядом цієї рекурентної формули. Деякі з них використовують не одне, а декілька відомих попередніх значень (x_i, x_i1, x_i2,).

3. За допомогою циклічного використання рекурентної формули визначаються всі необхідні значення x_i при відповідних значеннях аргументу t_i.

Числові методи дозволяють знаходити лише частинні розв’язки диференційних рівнянь при заданих початкових умовах. Найпростішим і найменш точним числовим методом розв’язування диференційних рівнянь є метод Ейлера першого порядку. Для автономних рівнянь цей метод реалізується рекурентною формулою

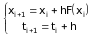. (5)

Наприклад, для рівняння dxdt=F(x)=3x², x(t₀)=0 ітераційна формула буде мати такий вигляд:

x_i+1=x_i+h3x_i², x₀=0.

Метод трапецій - одна з модифікацій методу Ейлера другого порядку. Він реалізується застосуванням на кожному кроці формули

x_i+1=x_i+(k₁+k₂)h2, (6)

де k₁=F(x_i), k₂=F(x_i+hk₁).