9.3.4Запис тексту програми.
Для полегшення процесу налагодження та введення даних користувачем необхідно реалізувати введення раніше підготованих даних (оператори READ, DATA в Бейсіку, використання файлу вхідних даних в Паскалі).
При програмній реалізації перестановки місцями (обміну) двох елементів масиву необхідно ввести допоміжну змінну і здійснити циклічну пересилку значень. При виконанні додаткового завдання використати функції RND(1) для Бейсіка або random(1) для Паскаля, які приймають випадкові значення з проміжку [0,1].
9.3.5Результати тестування і налагодження.
MIN A=0 MAX A=9
ГРУПА: 3 7 6 4 2 3 1 8 1 4
ВПОРЯДКОВАНА: 1 1 2 3 3 4 4 6 7 8
МІN ГРУПИ 1 МАХ ГРУПИ 8
Рис. 9.1. Приклад блок-схеми алгоритму сортування даних.
10.Лабораторна робота №10
Деякі задачі матричної алгебри
Мета роботи — засвоїти методи створення, доступу та використання базового структурованого типу даних — масивів, програмну реалізацію операцій з матрицями.
10.1Перелік питань, які необхідно вивчити.
10.1.1Визначення:
Транспонована матриця | аik |T = | aki |
Слід матриці
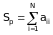
Множення матриці на число | aik |b = | aik*b|
Множення матриць C = А*В =
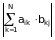
Додавання матриць А+В = | аik + bik |
10.1.2Необхідні питання з програмування:
Кероване виведення даних (оператори LOCATE або GoToXY);
Програмна реалізація вкладених циклів;
Введення раніше підготованих даних.
10.2Завдання.
Скласти програму, яка б виконувала задані операції із заданими матрицями.
Варіанти завдань до лабораторної роботи №10 наведено в Табл. 10 .1.
Табл. 10.1. Варіанти завдань до лабораторної роботи №10.
№ |
Вхідні матриці6
|
Вихідна матриця |
|
|
А |
В |
|
1 |
2 |
11 |
A*B |
2 |
1 |
3 |
A |
3 |
16 |
15 |
B*A |
4 |
15 |
3 |
A*SpB |
5 |
3 |
4 |
A+B |
6 |
4 |
12 |
SpA*B |
7 |
5 |
16 |
A+B |
8 |
16 |
3 |
A |
9 |
4 |
2 |
A |
10 |
7 |
5 |
A*B |
11 |
5 |
10 |
B*A |
12 |
6 |
14 |
A |
13 |
16 |
13 |
A*B |
14 |
10 |
5 |
A*B |
15 |
8 |
9 |
A*B |
16 |
11 |
12 |
A |
Табл. 10.2. Матриці до Табл. 10 .1.
Матриця № |
7 |
8 |
9 |
10 |
|
|6 25 11|
|
|1 8 10 -5| |
|3 1 9 7| |
|21 3 -15| |
Матриця № |
11 |
12 |
13 |
14 |
|
|
|
|
|
Матриця № |
15 |
16 |
|
|
|
|
|
|
|
10.3Приклад виконання тесту.
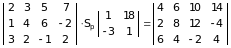
11.Лабораторна робота №11
Матричний опис резистивних схем.
Мета роботи — засвоїти методи створення, доступу та використання базового структурованого типу даних — масивів, записів, вивчити метод Гауса обчислення визначника матриці.
11.1Теоретичні відомості.
11.1.1Правила формування матриці вузлових провідностей.
Вузлом називають місце з’єднання двох чи більше елементів. Провідність – величина обернена до опору: Y=1/Z (Z–комплексний опір, для резистивних схем Z=R).
Матриця вузлових провідностей є квадратною матрицею, номери рядків і стовпців якої відповідають номерам вузлів схеми, кожний діагональний елемент є сумою провідностей елементів, з’єднаних з цим вузлом. Недіагональні елементи дорівнюють провідності елементів безпосередньо між відповідними вузлами, взятій з протилежним знаком. Матриця провідності лінійної (в тому числі резистивної) схеми є симетричною відносно головної діагоналі. Приклад схеми та її матриці вузлових провідностей наведено на Рис. 11 .1. Матриця вузлових провідностей без нульових рядка та стовпця (вони можуть бути утворені як сума решти рядків та стовпців, а отже з ними визначник цієї матриці рівний нулю) повністю описує відповідну схему.
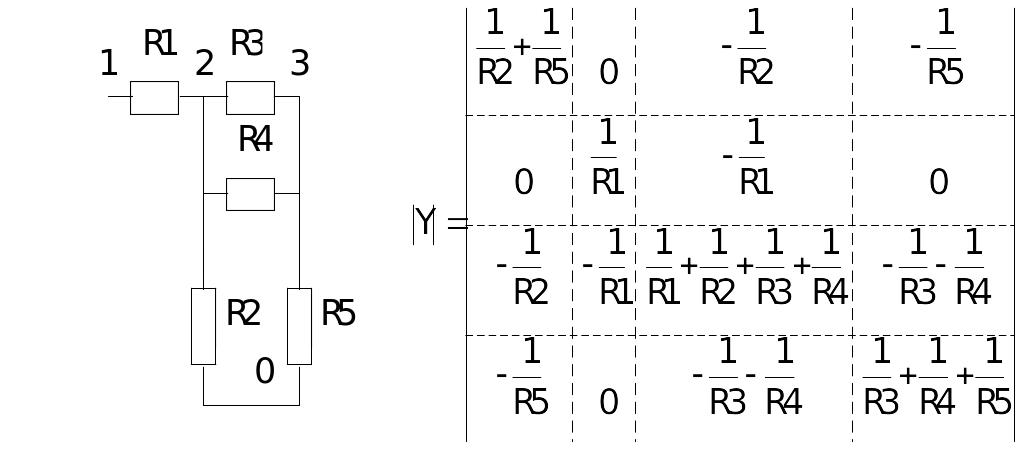
Рис. 11.1. Схема та її матриця вузлових провідностей.