7.3Приклад виконання завдання.

Задано функцію f(x)=e^x= і значення: x=2.85; =0.0001.

7.3.1Постановка задачі.

З метою оптимізації програми за часом виконання і кількістю виконуваних операцій необхідно визначити кожний член ряду а_n не безпосередньо за формулою, яка вимагає циклу для обчислення n! та “повільної” операції піднесення до степеня, а через відоме значення попереднього члену а_n-1, тобто за рекурентною формулою. Для виведення рекурентної формули в вираз для а_n підставимо n=n-1 та домножимо отриманий вираз так, щоб в результаті скорочень одержати вираз для а_n:

,

та знайдемо значення нульового члену ряду:

а₀=x⁰0!=11=1.

7.3.2Розробка структури даних.

Приклад розробки структури даних подано в Табл. 7 .3.

Табл. 7.3. Структура даних програми.

Позначення	Ім’я	Тип	Призначення, опис
x	x	дійсна	аргумент вхідна
f	F	дійсна	значення функції вихідна
n	n0	ціла константа	номер першого члену ряду, n0=0
n	n	ціла	номер члену ряду
аn	a	дійсна	n-й член ряду
	d	дійсна константа	похибка обчислення суми ряду
–	S	дійсна	сума ряду вихідна

7.3.3Розробка алгоритму

Оскільки необхідна кількість членів ряду невідома наперед, то необхідно використовувати цикли “до” або “поки” з виходом з них по досягненню заданої точності обчислень Треба відвести змінну для накопичення суми членів ряду, яку перед початком циклу потрібно обнулити. Для порівняння заданої та досягнутої похибок треба розрахувати f(x). Спрощена блок-схема алгоритму обчислень наведена на Рис. 7 .1.

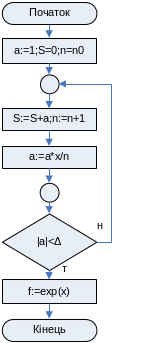
Рис. 7.1. Блок-схема алгоритму обчислення суми функціонального ряду.

На блок-схемі відсутні команди введення та виведення даних, які розміщуються студентом самостійно при виконанні роботи. Алгоритм використовує керуючу структуру “цикл до”. На блок-схемі відмічена контрольна точка КТ1, в якій зручно розмістити проміжний вивід для спостереження за ходом виконання програми, за збіжністю ряду при налагоджені програми.

7.3.4Текст програми мовою Pascal.

program RJAD;

const

n0: shortint=0;

d: real =1e-4;

var

x, a, F, S: real;

n: byte;

BEGIN

writeln (‘Введіть значення аргументу x’);

readln (x); {введення значення x}

a:=1; S:=0; n:=n0; {початкові значення змінних}

repeat {початок циклу “до”}

S:=S+a; {накопичення суми ряду}

n:=n+1; a:=a*x/n; {значення наступного члену}

writeln (n:4, a:12:5, S:12:5); {проміжний друк}

until abs(a)<d;{умова виходу з циклу “до”}

F:=exp(x); {значення функції}

writeln (‘сума ряду’, S:12:5, ‘функція’:15, F:12:5); {виведення}

writeln (‘Похибки: Задана’, d:8);

writeln (‘досягнута’:15, abs(F-S):8);

END.

7.3.5НАлагодження і результати тестування.

Відмічаються помилки та відповідні корекції алгоритму та тексту програми. Студенти наводять висновки про швидкість збіжності функціонального ряду, отримані на підставі виведених проміжних результатів. Порівнюється задана та досягнена точність розрахунків, наводяться результати роботи програми при декількох значеннях аргументу.

8.Лабораторна робота №8

Табулювання функції, заданої рядом Фур’є.

Мета роботи - засвоїти методику та виробити практичні навики застотування вкладених циклів.

8.1Перелік питань, які необхідно вивчити

• Програмна реалізація табулювання функцій;

• Обчислення суми ряду;

• Правила запису вкладених циклів;

• Поняття про періодичну функцію.

8.2Завдання.

Протабулювати функцію y=f(t) для М значень аргумента на інтервалі [a,b]. Функція задана аналітично та у вигляді ряду Фур’є:

.

Приклад графіка функції заданої аналітично та у вигляді суми перших трьох членів ряду Фур’є наведено на Рис. 8 .1.

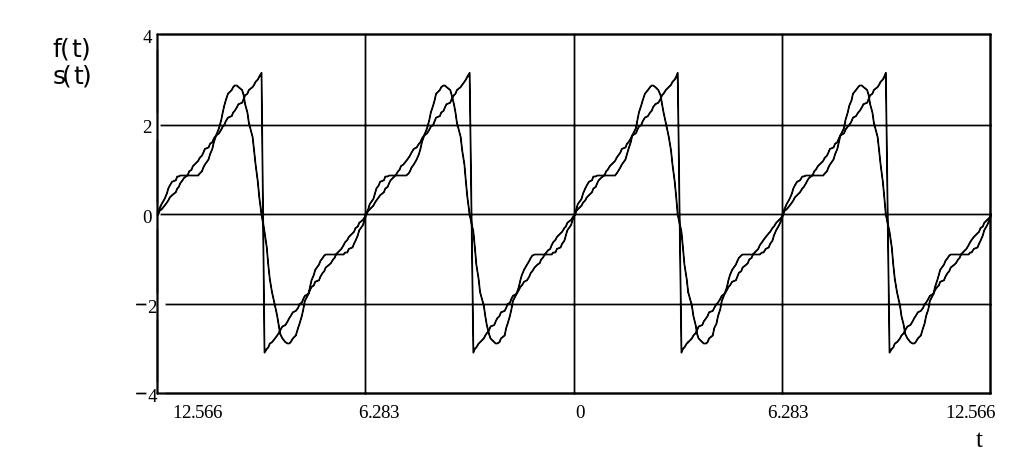
Рис. 8.1. Графіки функцій побудованих на основі результатів табулювання.

Варіанти завдань до лабораторної роботи №8 подано в Табл. 8 .1. При розрахунку врахувати N перших членів ряду. Не вказані в таблиці коефіцієнти a_k, b_k дорівнюють нулеві.

Табл. 8.1. Варіанти завдань до лабораторної роботи.

№	f(t)		ak, bk			a	b	M	N
1		[(t+) mod 2] 3		bk=2(-1)k+1k		-1.5	1.5	20	8
2		|F1 |4		ak=	(парні k) (непарні k)	0	2	16	5
3		(t mod 2)­		bk= -2k				8	3
4				bk=	(парні k) (непарні k)	-2	32	16	7
5		5sign(t) 5		bk=	(парні k) (непарні k)	-		20	15
6				bk=	(парні k) (непарні k)	0	2	18	17
7				bk=	(парні k) (непарні k)	0		20	15
8		t223		ak=(-1)k4k2		-		15	7
9		t(t)26		ak=	(парні k) (непарні k)	0		10	10
10		t(t)sign(t)		bk=	(парні k) (непарні k)	-2	2	20	8
11		|sin(t)|2			(парні k) (непарні k)	0	32	15	6
12		cos(t mod )			(парні k) (непарні k)	0	2	20	10
13		-1/ (t<0, t> ) sin(t)-1/ (0≤t≤)		b1=12	(парні k) (непарні k)	-2	32	16	10
14		F1cos(t)		b1=-12 bk=(-1)k2k(k21)		-	2	18	7
15		F1sin(t)1		a1=-12 ak=-2(-1)k(k21)		-2		18	5
16		(3t26t+22)12		ak=1k2		0	2	20	3
17		(t)2		bk=1k		0	2	16	9