Метод Ньютона Как обобщенный градиентный метод (Методические указания)
Челябинск, 1992 г.
Методические указания составлен в помощь студентам четвертого курса математического факультета, изучающим курс “Методы оптимизации”.
Длинная работа является руководством при проведении занятий по темам “Градиентные методы”, “Методы переменной метрики” и “Метод Ньютона” в курсе “Методы оптимизации”. Приведен ряд упражнений, разъясняющих связь, структуру и особенности методов с единой позиции.
§1 Обобщенный градиентный метод в задаче безусловной оптимизации
Пусть функция f(x) является гладкой функцией на всем пространстве Rn. Численный поиск точки локального минимума этой функции сводится к следующей схеме:
где
– два
последующих приближения искомой точки,
> 0 –длина шага в направлении
Если вектор ξk
является
направление
спуска (см.
рис 1), т.е..
< 0 для
≠
0 и
= 0 для
=
0, то процесс (1.1) называется обобщенным
градиентным методом
[I].
(Здесь и далее через
обозначается вектор градиента функции
,
вычисленный в точке
штрихом
вверху –
транспонирование). При этом, если для
любой сходящейся под последовательности
{
}<
{
}
такой, что
≠ 0, выполняется соотношение:
0 <
|
|,
||
||
< +∞,
(1.2)
то последовательно { } называют равномерно градиентной относительно последовательности { }.
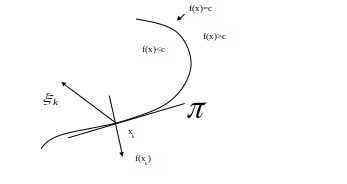
Рис.I.
Градиент
и вектор спуска
направлены в различные полупространства,
определяемые гиперплоскостью
–
касательной к линии
уровня
=c=const
в точке
.
По существу, условия
(1.2) обеспечивают ограниченность
последовательности {
}
и исключают взаимную ортогональность
векторов
и
в пределе.
Упражнение I.
Доказать, что последовательность {
}
будет равномерно градиентной, если для
всех
выполняются условия:
||
|| ≤ С2
||
||P
,
C1||
||P
≤ -
,
(1.3)
где числа C1>0, C2>0, P1≥0, P2≥ 0.
Упражнение 2. Доказать, что для
= - Dk , (1.4)
где Dk – положительно определенная симметричная матрица такая, что
C1||
||P
||Z||
2≤
С2 ||
||P
||Z||2
,
Z
Rn
(1.5)
Выполняется условия типа (1.3)
Пример 1. Последовательность { } , построенная градиентным методом:
, = - , (1.6)
является равномерно градиентной. В том легко убедиться, если положить в (1.5)
Dk = E ( E – единичная матрица ).
Конкретная
реализация обобщенного градиентного
метода (1.1) определяется способами выбора
шагового множителя
и
направления спуска
.
Примерами таких широко применяемых на
практике реализаций служит градиентный
метод, метод Ньютона, квазиньютоновские
методы, методы сопряженных градиентов
и многие их модификации [1,2,3,4,5,6,7].
Выбор шагового множителя обычно осуществляют одним из следующих способов [1, 5 ].
1 Правило Армийс.
При фиксированных
значениях числовых параметров
и
полагают
=
,
где
- наименьшее из неотрицательных целых
чисел
,
для которых
≥-
.
2 Правило Голдстейна
При фиксированном шаговый множитель выбирают из условия:
3 Одномерная минимизация.
Параметр выбирают из условия:
,
(1.7)
Где
–
максимально допустимая длина шага.
Обычно для решения (1.7) используется численные алгоритмы одномерного поиска [3,5,6,7]. Тогда, например, одномерную минимизацию можно завершить при выполнении неравенств (объясните почему):
(1.8)
где
и
- заданные числа из неравенства (0;1)
(параметр
чаще всего берут близким к 0, например,
см.упр.4)
4.Постоянный шаговый множитель.
Полагают
=
при
все
k.
Упражнение 3.
Указать промежутки значений шагового
множителя
,
изображенные на рис.2 и удовлетворяющие
а) правилу Армийо; б) правилу Голдстейна.
0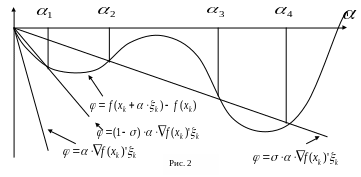
Утверждение 1. 1) g : R R, g( ) c1(R).
2)
M
R,
|M|<+
: g(
)≥M
R,
3) 0< < <1,
4)
g′(0)
= dg/d
|
<0,
1)-4)
0<c1<c2
:
[c1;c2]
выполнены неравенства:
g(0)-g(
)
≥ -
g′(0),
| g’( )|≤ ∙|g′(0)|.
Доказательство: Зафиксируем любое число r : <r< .
Обозначим A={ ≥0: r∙g′(0)≤g′( )≤0} . Это множество непустое, так как g′( )<0 и g( ) c1(R).
Пусть
=inf{
:
A}.
>0
так как r∙g′(0)>g′(0).
Тогда в силу определения для [0; ] выполнено неравенство:
g′( )≤ r∙g′(0). (1.9)
Следовательно,
(0;
):
| g′(
)|
≤
|
g′(
)|
для
[
-
;
+
]
(см. рис. 3)
Рис. 3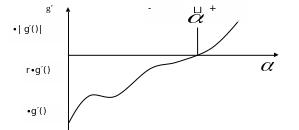
С учетом (1,9) получим:
g(
)=g(0)
+
g′(
)d
≤g(0)
+ r∙
g′(0)∙
<g(0)
+
∙
g′(0)∙
.
Поэтому в силу
непрерывности функции g(
)
(0;
);
g(
)
– g(0)≤
∙
g′(0)∙
при
[
-
;
+
]
(см. рис. 4)
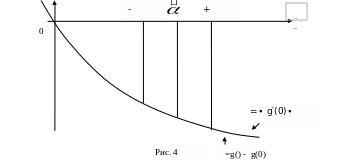
Полагая
=
min{
}
и c1
=
-
,
c2
=
+
,
получим требуемое утверждение.
Упражнение 4.
Используя утверждение 1 доказать, что
если функция
ограничена снизу на Rn,
<
0,
*
= +
,
а параметры
и
выбраны так, что 0<
<
<1,
то найдутся числа 0<c1<
c2
такие, что для любого
[c1,c2]
условия (1,8) будут выполнены.
Упражнение 5. Пусть { } - последовательность, построенная обобщенным градиентным методом (1.1), и { } является равномерно градиентной относительно { } последовательностью. Доказать, что если
{
}
{
}:
x*
и
f(x*)
≠ 0, то
0
при выборе шагового множителя по правилу Армийо.
Теорема 1.
1) f: Rn R, f(x) c1(Rn)
2){ } - последовательность, построенная обобщенным градиентным методом (1.1)
3){ } - равномерно градиентная относительно последовательность
4){ } - построена по правилу Армийо.
1)-4)
Любая предельная точка
*
последовательности {
}
является точкой
стационарности функции f(x)
,т.е.
=0.
*Упражнение 6. Используя упражнение 5 доказать теорему 1.
*Упражнение 7. Доказать теорему 1 при выборе шагового множителя и одномерной минимизации с *= , из правила Голдстейна и из соотношений (1.8)
Указание: При доказательстве использовать неравенство:
,
где
= xk
+
и
определено в результате одномерной
минимизации, а
=
xk
и
- из правила Армийо.
Теорема 1 позволяет ввести следующее правило для окончания итерационного процесса (1.1). Вычисления прекращаются, если полученная на очередной итерации точка xk удовлетворяет неравенству:
||
||
≤
(1.10)
где - достаточно малое положительное число.
На практике такая точка обычно отождествляется с точкой стационарности функции f(x).
Упражнении 8.
Доказать, что если для некоторых чисел
c1
> 0, c2
> 0, p1
> 0, p2
> 0 и
любого выполнены условия (1.3), то при
определенных соотношения между числами
и
критерий (1.10) окончания процесса (1.1)
эквивалентен критерию:
≤
.
Упражнение 9.
Пусть
*
- такая точка локального минимума функции
,
что при некоторых
>0,
>0
и для
O
(
- окрестность точки
*)
имеет место неравенство:
,
Rn,
где
-
(
)
- матрица вторых производных (матрица
Гессе) функции
,
вычисленная в точке
.
Доказать, что для
O
такого, что
верны оценки:
,
.