Правила дифференцирования

1. Производная постоянной функции равна нулю: с' = 0.

2 . Постоянный множитель можно выносить: (сu)' = cu' . 3. Производная суммы равна сумме производных: ( u + v )' = u' + v'.

4. Производная произведения: ( uv)' = u'v + uv'.

Пример 2. Найти производные следующих функций.

1). y = 2х³ 5x² + 7x + 4.

Последовательно применяются правила дифференцирования 3, 2, 1 и формула 1 из таблицы производных: у' = (2х³)' (5x²)' + (7x)' + (4)' =

2 (х³)' 5(x²)' + 7(x)' + 0 = 23х² 52x¹ + 71 = 6х² 10x + 7.

2). у = х²е ^х.

Применяются правило 4 и формулы 1, 2 из таблицы производных:

у' = (х²)'е ^х + х²(е ^х)' = 2х¹е ^х + х²е ^х = хе ^х(2+х).

3). у = хx(lnx2).

В ыражение хx переписывается как , тогда у = (lnx 2). Применяются правило 4 и формулы 1, 3 из таблицы производных:

у' = (х^3/2)'(lnx 2) + х^3/2(lnx 2)' = (3/2)(х^1/2)(lnx 2) + х^3/2(l/x 0) = 1,5x^.lnx 2x.

Следующее правило применяется при вычислении производной сложной функции.

Пусть F(x) = (fg)(x) = f(g(x)) суперпозиция двух функций f(u) и g(x). При этом f(u)  внешняя функция, g(x)  внутренняя функция, буква u  промежуточный аргумент. И пусть существуют: g_x'(x₀)  производная внутренней функции в точке x₀ и f_u '(u₀)производная внешней функции точке u₀ = g(x₀). Тогда существует F '(x₀) - производная сложной функции F(x) в точке x₀ и выполняется равенство:

F '(x₀) = f_u'(u₀) g_x'(x₀). (44)

Другими словами, производная сложной функции равна произведению прозводной внешней функции по промежуточному аргументу на производную внутренней функции.

Пример 3. Вычислить производные следующих функций.

1). y = log₃ (5x²+3).

Здесь log₃ (5x²+3)  сложная функция: u = (5x²+3)  внутренняя и у =

log₃u  внешняя функции. По формуле 3, (log₃ u)' = 1/ (uln3), а (5x²+3) =

= (10x+0) = 10x. Тогда, по формуле (44),

Здесь u = 1 – х²  внутренняя функция и у =u  внешняя функция.

Т огда 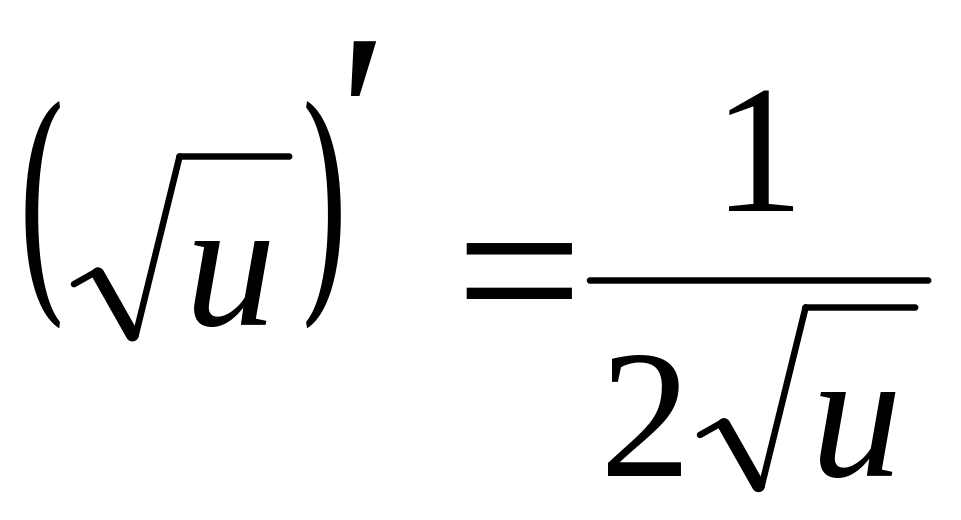и u = (1 - x²) = 2x. Следовательно,

З десь u =  x²  внутренняя и у = e^u  внешняя функции. Тогда (e^u)' = e^u, и ( x²) = 2x. Следовательно, по формуле (44), y= e^u (2x) = 2x .

4). y = x⁴ (8ln²x 4lnx + 1).

П о правилу 3, y' = (x⁴)'(8ln²x 4lnx + 1) + x⁴(8ln²x 4lnx + 1)' = 4x³(8ln²x 4lnx + 1) + x⁴(82lnx(1/x) 4(1/x) + 0) = 32x³ln²x.

И з свойств логарифмов следует: y = (2/3)(ln(13x) ln(1+3x)).

В следующем примере применяется так называемый метод логарифмического дифференцирования. Если исходная функция y = f(x) получена с помощью операций умножения, деления, возведения в степень или извлечения корня, то сначала находят логарифм этой функции: lny = lnf(x), при этом правую часть преобразуют с помощью соответствующих свойств логарифмов. Затем находят производные от обеих частей полученного равенства, при этом считают, что (ln y)= . Из вновь полученного равенства выделяют искомую производную у.

Сначала логарифмируют обе части исходного равенства:

Т еперь, дифференцируют это равенство:

Производная у  = f (x) называется производной 1-го порядка. И ее можно рассматривать как функцию от х. Тогда производная от f (x) называется производной 2-го порядка и обозначается через у = f (x). Это понятие распространяется на все натуральные числа следующим образом.

Определение 2. Производной n-го порядка от функции f (x) по х называется производная по х от ее производной (n-1)-го порядка, (обозначение:

y ⁽ⁿ⁾ = f⁽ⁿ⁾(x)).

Пример 4. Найти производные второго и третьего порядков.

1). y = x lnx.

Решение. Сначала находится производная 1-го порядка: y = x lnx +

х lnx = 1 lnx + x 1/х = lnx + 1. От полученной функции снова берется производная: y = lnx+ 1= 1/х + 0 = 1/х. Аналогично, y⁽³⁾ = (1/х)= 1/х².

2). y = x³ e^x .

Решение. у = х³ е^х + х³ е^х = 3х² е^х + х³ е^х= е^х (3х² + х³) ; у =

e^x (3x² + x³) + e^x (3x² + x³) = e^x (3x² + x³) + e^x (6x +3x²) = e^x (6x² + x³ + 6x);

у⁽³⁾ = е^х (6х² + х³ + 6х) + е^х (6х² + х³+ 6х) = е^х (9х² + х³ +18х + 6).