
- •Глава 6. Дифференциальное исчисление
- •§1. Производная функции
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функции
- •§3. Дифференциал функции
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Исследование функции на вогнутость и точки перегиба
- •Построение графиков функций
- •Упражнения
Глава 6. Дифференциальное исчисление
Важнейшим понятием современной математики является понятие производной функции. Оно возникло как результат многовековых усилий, направленных на решение задачи о касательной к данной кривой, задачи о скорости неравномерного движения и некоторых других задач. Подобные задачи интересовали математиков с давних времен, и накопившийся в этом направлении обширный материал получил теоретическое завершение лишь в 17 веке в трудах Ньютона и Лейбница.
§1. Производная функции
Пусть функция у = f(x) определена во всех точках некоторого интервала (а; b) и точка хо принадлежит этому интервалу. Пусть х другая точка из (а; b), тогда разность х = х хо называется приращением аргумента в точке хо, и разность у = f(x) f(xo) называется приращением функции f(x) в точке хо, соответствующим приращению х.
О![]() пределение
1.
Производной
функции
у = f(x) в точке
хо
называется предел отношения у
к
х
в точке хо,
когда х
стремится к нулю, если этот предел
существует, (обозначения:
f
(x0),
y(x0),
пределение
1.
Производной
функции
у = f(x) в точке
хо
называется предел отношения у
к
х
в точке хо,
когда х
стремится к нулю, если этот предел
существует, (обозначения:
f
(x0),
y(x0),
![]() ,
,
![]() ).
).
Пример 1. 1). Вычислить производную функции у = х3 в точке хо = 2.
Р![]() ешение.
По условию, х
= (х
2)
и у
=
(х323).
Тогда
ешение.
По условию, х
= (х
2)
и у
=
(х323).
Тогда
Ответ: y (2) = 12.
2). Вычислить производную функции у = lnx в точке хо = 1.
Р![]() ешение.
По условию, х
= (х
1)
и у
=
(lnx
ln1).
Последнее выражение преобразовывается
следующим образом: у
=
ln
x
ln(1
+ x
1)
=
ешение.
По условию, х
= (х
1)
и у
=
(lnx
ln1).
Последнее выражение преобразовывается
следующим образом: у
=
ln
x
ln(1
+ x
1)
=
Ответ: y (2) = 12.
Если конкретная точка х0 не указана, то производные записываются в общем виде для произвольного х так как это сделано в следующей таблице.
Таблица производных простейших функций
-
№
Функция
Производная
Частные случаи
1
x
x
1' = 0; x' = 1; (х2)' = 2x;
 ;
;

2
ах
ахlna
(amx)' = mamxlna; (еmx)' = memx.
3
logax



4
sinx
cosx
(sin(mx)) = m cos(mx).
5
cosx
sinx
(cos(mx)) = m sin(mx).
6
tgx

(tg(mx)) =
 .
.7
ctgx

(ctg(mx)) =
 .
.8
arcsinx

(arcsin(mx)) =

9
arccosx

(arcos(mx)) =

10
arctgx
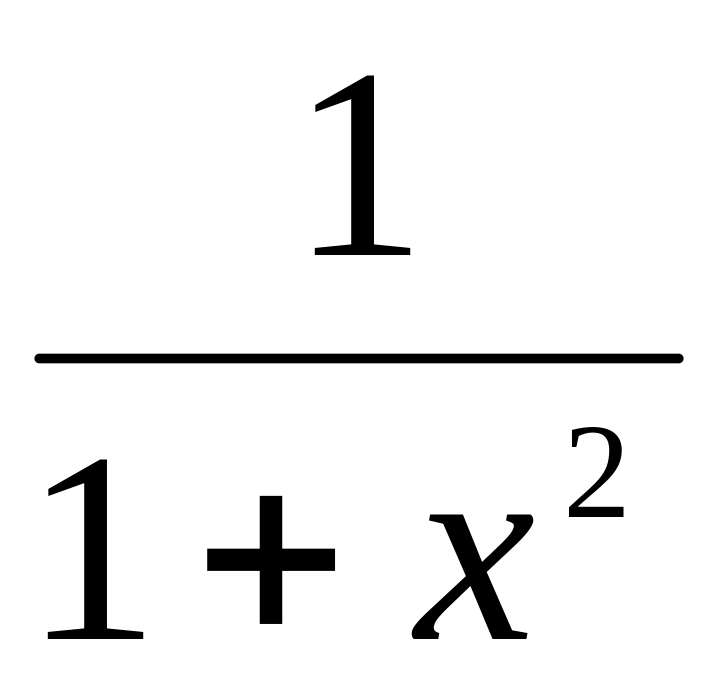
(arctg(mx)) =

11
arcctgx

(arcctg(mx)) =
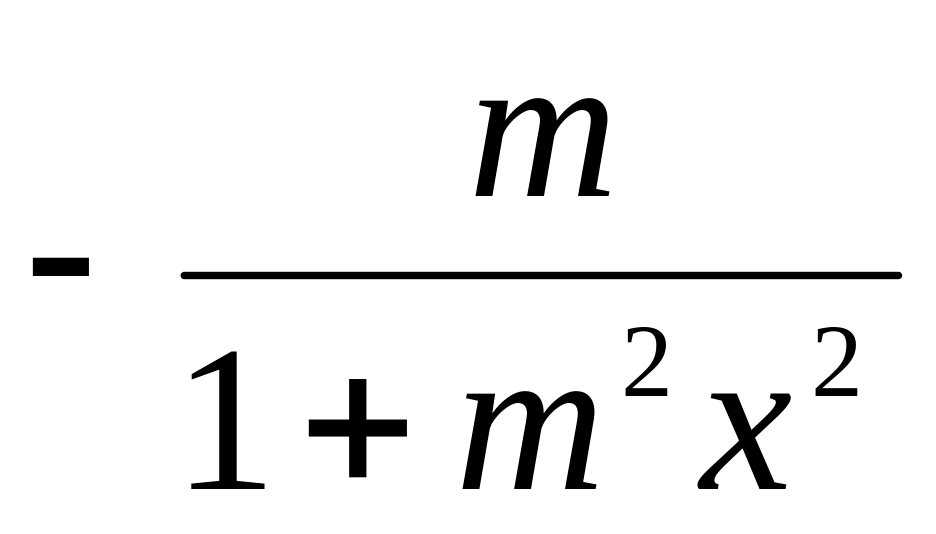
Доказательства этих формул и следующих правил предлагается читателю рассмотреть самостоятельно [8, с. 54].
