Основные свойства логарифмов

1). Основное логарифмическое тождество:

2). Логарифм от 1 равен нулю:

3). Логарифм от основания равен единице:

4). Логарифм произведения равен сумме логарифмов:

5). Логарифм дроби равен разности логарифмов:

6). При логарифмировании степени логарифм умножается на ее показатель:

7). При логарифмировании корня логарифм делится на показатель корня:

5. Логарифмической функцией называется функция вида у= log_ax, которая каждому значению х ставит в соответствие логарифм по основанию а от х. Основание а является положительным и не равно единице.

Областью определения логарифмической функции log_ax является проме­жуток (0; + ); она неограниченная и может принимать любые значения от  до +. При а > 1 функция log_ax возрастает от  до + (в этом случае пишут: log_a0 =  и log_a(+ = +. При а < 1 функция log_ax, убывает от + до  (т.е. log_a0 = + и log_a(+ = ).

у

Таблица значений

x y₁ y₂

0,25 -2 2

0,5 -1 1

1 0 0

2 1 -1

4 2 -2

8 3 -3

3

2 y₁ = log₂x

1

x

0 1 2 3 4 5 6 7 8

-1

-2 y₂ = log_0,5x

-3

Черт.25.

При основании а = е  2,72 логарифмы log_еx называются натуральными и обозначаются ln x . График функции у = ln x пересекает ось Ох под углом 45^о.

6. Тригонометрические функции. В декартовой системе координат XOY строится окружность с центром в начале координат и радиусом 1. На окружности берется точка М, в нее из центра проводится радиус-вектор . Буквой  обозначается угол, образованный вектором с осью ОХ.

1) синусом угла  называется ордината точки М, обозначение: sin ;

2) косинусом угла  называется абсцисса точки М, обозначение: cos;

3) тангенсом угла  называется отношение sinк сos если сos  0, обозначение: tg;

4) котангенсом угла  называется отношение сos к sin если sin  0, обозначение: ctg.

Y

M(cos; sin)

 0 X

2

Черт.26.

Из пунктов 1), 2) данного определения следует, что значения функций sin и cos заключены в промежутке [1; 1]: 1 sin 1 и 1 сos  1. Кроме того, эти значения повторяются, когда точка М делает полный оборот по окружности, т.е. sin(+ sinи сos( сos. При  = 0⁰ точка М занимает крайнее правое положение, и ее координаты равны (1; 0), поэтому

сos0⁰ 1 и sin0⁰= 0. При этом tg0⁰ = =0, но значение сtg0⁰ не определено. При  = 90⁰ точкам М занимает верхнее положение, и ее координаты равны (0; 1), поэтому сos90⁰ 0 и sin90⁰= 1. При этом сtg90⁰ = =0, но значение tg90⁰ не определено. Аналогично находятся значения данных функций в других точках. В следующей таблице приведены основные значения этих функций.

Между собой данные функции связаны следующими равенствами, которые называются основными тригонометрическими тождествами:

sin²+ сos² 1; 1+ tg²= ; 1+сtg²  tg= ; ctg=

 	900	600	450	300	00	300	450	600	900	1200	1350	1500	1800
													 
sin	1				0				1				0
cos	0				1				0				 1
tg					0		1				1		0
ctg	0		1				1		0		1		

Следующие формулы часто используются для преобразования сложных тригонометрических выражений.

Формулы приведения:

Формулы понижения степени:

сos² sin² 

sinсos ; cos² sin²cos2

Формулы преобразования произведения в сумму:

sinсos 

cosсos 

sinsin .

Теперь определяются числовые тригонометрические функции.

Функцией y = sinx называется отображение, при котором каждому

значению х ставится в соответствие синус угла в х радиан. Областью определения этой функции является (; ), область значений [1; 1]. Как было отмечено выше, sinx – периодическая функция с наименьшим положительным периодом 2Ее график имеет следующий вид.

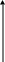y

₁

_. x

^1

Черт.27.

Функцией y = cosx называется отображение, при котором каждому значению х ставится в соответствие косинус угла в х радиан. Областью определения этой функции является (; ), область значений [1; 1]. Как было отмечено выше, сosx – периодическая функция с наименьшим положительным периодом 2Ее график имеет следующий вид.

y

₁

_. x

^1

Черт. 28.

Функцией y = tgx называется отображение, при котором каждому значению х ставится в соответствие тангенс угла в х радиан. Областью определения этой функции являются интервалы вида , kZ. Область значений (; ). Функция tgx также периодическая и ее наименьший положительный период равен :  tg(x+) = tgx.Ее график изображен на следующем чертеже.

у

_. x

Черт.29.

7. Обратные тригонометрические функции.

Арксинусом числа х называется угол , расположенный в промежутке и синус которого равен х, обозначение: arcsin x.

Арккосинусом числа х называется угол , расположенный в промежутке и косинус которого равен х, обозначение: arcos x.

Арктангенсом числа х называется угол , расположенный в промежутке и тангенс которого равен х, обозначение: arctg x.

Арккотангенсом числа х называется угол , расположенный в промежутке и котангенс которого равен х, обозначение: arcctg x.

Согласно данным определениям выполняются следующие тождества:

sin(arcsin x)  x, cos(arcos x)  x, tg(arctg x)  x, ctg(arcctg x)  x.

Также как в пункте 6 определяются числовые функции:

у = у = у = у = .

Графики этих функций показаны на чертеже 30.

у у

х

^{-1 0 1}

1 0 1 х

а) у = б) у =

у у

х

^{-1 0 1}

1 0 1 х

в) у = г) у =

Черт.30.

К простейшим функциям относятся степенные, показательные, логариф­мические, а также тригонометрические и обратные тригонометрические функ­ции.

Определение 7. Элементарными функциями называются простей­шие функции и все функции, получаемые из простейших с помощью конечного числа применений операций сложения, вычитания, произведения, деления и суперпозиции.

В следующем примере указаны элементарные функции, которые описы­вают зависимости между некоторыми реальными величинами в соответствую­щих областях экономики.

Пример 8. 1). Зависимость спроса у на некоторый товар от его цены х может иметь вид: или у = 6е^-3х.

В случае дефицитного товара зависимость спроса у от времени t может быть описана логистической функцией (где k, p, a – специальные числа):

2). Зависимость выручки у от спроса х на некоторый товар может иметь вид дробно-рациональной функции

3). Зависимость издержек производства f(x) от объема производства x имеет вид линейной функции, например: f(x) = 5х+300. Зависимость себе­стоимости g(x) от объема производства и издержек производства следующая g(x) = . Тогда зависимость себе­стоимости от объема x принимает вид: g(x) = 5+ .

4). Прогноз численности населения можно производить по формулам у = bt + c и у = cа^t, где c  исходная численность, b  средний абсолютный при­рост, а  средний темп роста, t  период, на который делается прогноз.

5). Рентабельность у связана с себестоимостью продукции х зависимо­стью у = 1, где m  цена продукции.

6). Распределение дохода в обществе c рыночной экономикой описыва­ется законом Парето: y = ax^m, где у  число лиц, имеющих доход, не меньший х, и m, a – положительные постоянные, например: a = 210⁹, m = 1,5.

7). Зависимость суммы вклада S под сложный процент от времени t

хране­ния вклада определяется формулой , где S₀  первоначальный вклад, m%  процентная ставка .

8). Нормальный закон распределения вероятностей играет важную роль в статистике, он задается функцией плотности f(x) вида сложно-показательной функции .