§2. Простейшие функции

1. Степенной функцией называется функция вида у = х^, которая каж­дому значению аргумента х ставит в соответствие х в степени .

Пример 5. Графики следующих степенных функций представлены на черт. 23:

а) у = х, б) у = х^, в) у = х³, г) у = = , д) у = = x^, е) y = = x^.

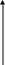
y y y

x x x

_{0 0 0}

a) б) в)

y y у

x x х

^{0 0 0}

г) д) е)

Черт.23.

2. Действия со степенями. Для натурального числа n степенью аⁿ называется n-кратное умножение а на себя:

Для n = 0 полагают: а⁰ = 1. Для дробного показателя принято следующее соглашение: , т.е. корень n–й степени из a^m. Для отрицательного показателя (целого или дробного) полагают:

Пример 6. 1). 2⁵ = 32, 2¹⁰ = 1024, 3⁴ = 81, 4³ = 64, 15² = 225, 25² = 625.

2). 5⁰ = 1, х⁰ = 1,

Основные свойства степеней

1). При умножении степеней с одинаковым основанием показатели складываются:

2). При делении степеней с одинаковым основанием показатели вычитаются:

3). При возведении степени в степень показатели умножаются:

4). При извлечении корня из степени ее показатель делится на показатель корня:

3. Выше были определены степени для любого рационального числа х. Кроме того, имеются специальные соглашения для определения степени в случае иррационального показателя х (о них будет сказано в разделе «предел функции»). Тем самым, положительное число а можно возводить в степень с любым вещественным показателем. Это позволяет определить следующую функцию.

Показательной функцией называется функция вида у = а^х, которая ка­ждому значению х ставит в соответствие а в степени х. Число а называ­ется основанием, оно положительное и не равно единице: а > 0, а  1.

y

x y₁ y₂

3 0,12 8

2 0,25 4

1 0,5 2

0 1 1

1 2 0,5

2 4 0,25

3 8 0,12

y₂= 0,5^x 4 y₁= 2^x Таблица значений

3

2

1

x

-3 -2 -1 0 1 2 3

Черт.24.

Показательная функция всюду определенная: D_f = (; +; она всегда положительная (а^х > 0), и неограниченная (max а^х = +). При а > 1 функция

а^х возрастает от 0 до + (в этом случае пишут: а^ = 0 и а^+ = +. При а < 1 функция а^х убывает от + до 0 (т.е. а^ = + и а^+ = 0).

Особое значение имеет показательная функция e^x со специ­альным основанием е  2,72, эта функция называется экспонентой и обознача­ется у = exp(x) .

4. Логарифмы. Пусть а > 0, a  1 и N – некоторое положительное число.

Логарифмом числа N по основанию а называется показатель n степени, в которую нужно возвести а чтобы получить число N, обозначение:

Пример 7. 1). так как 2). так как