Лекция №7

Изменение физических величин во времени

Рассмотрим среднее значение физической величины L, изменяющееся во времени:

.

Вычислим производную

.

Заменим в этом выражении производные волновых функций через гамильтониан из уравнения Шредингера:

.

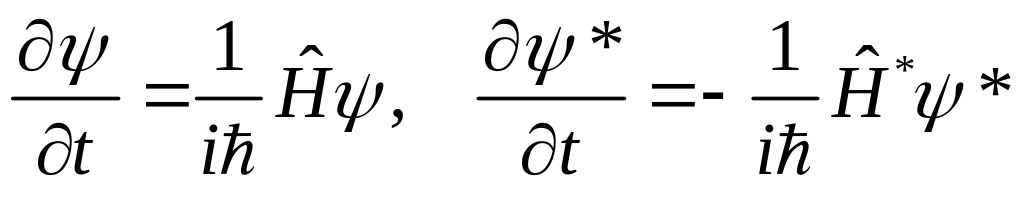Тогда

.

Преобразуем первый интеграл, воспользовавшись самосопряженностью гамильтониана:

,

что приводит к выражению

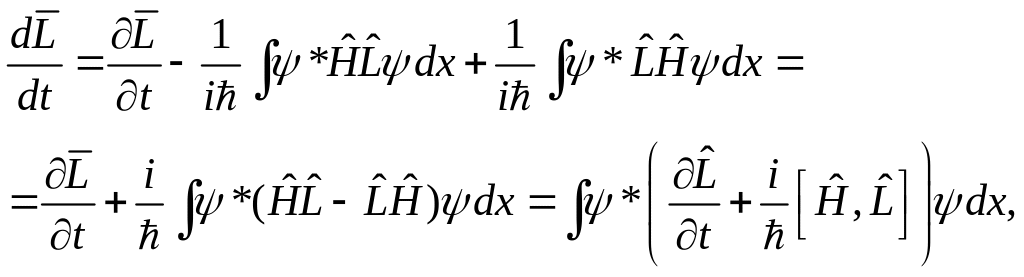
откуда получим выражение для производной оператора:

Определение

Если , то соответствующая физическая величина L называется сохраняющейся или интегралом движения.

Следствия:

1.Если оператор явно не зависит от времени, то есть , интегралом движения является величина, оператор которой коммутирует с , то есть

2. Положим , тогда, если гамильтониан не зависит от времени, то полная энергия системы сохраняется (замкнутая система).

Тождественность частиц. Бозоны и фермионы

В классической механике можно различить траектории движения электронов, например, в электронно-лучевой трубке. Но если электронно-лучевую трубку уменьшить до размеров, сравнимых с длиной волны Де Бройля, то определить траекторию движения конкретного электрона невозможно. Таким образом, в микромире, подчиняющемся квантовой механике, вследствие вероятностного описания движения невозможно точно идентифицировать частицы. Этот факт составляет содержание принципа неразличимости (тождественности) частиц.

Рассмотрим следствие данного принципа. Пусть производится перестановка двух частиц, описываемых волновой функцией (х₁, х₂). Тогда на основании принципа неразличимости состояний до и после перестановки, а также того, что волновая функция определена с точностью до множителя е^i , можно записать

.

Но в силу произвольности идентификации (нумерации) частиц справедлива также запись

.

Из этих двух равенств следует:

,

откуда

e^2ia=1 или e^ia= ±1,

или окончательно

. (7.1)

Это означает, что возможны два типа волновых функций — симметричные, соответствующие знаку “+” в (7.1), и антисимметричные, соответствующие знаку ““. В релятивистской квантовой механике показывается, что симметричные волновые функции описывают частицы со спиновым квантовым числом, принимающим целые значения (бозоны), а антисимметричные волновые функции — частицы с полуцелыми (кратными 1/2) значениями спинового квантового числа (фермионы).

Принцип Паули. Обменное взаимодействие

Пусть имеем систему из N частиц, не взаимодействующих между собой и находящихся в состояниях р₁,...,р_N. Для системы бозонов волновая функция N частиц (x₁,...x_N) выражается через одночастичные волновые функции на основании правила вычисления вероятности независимых событий в виде суммы N! всевозможных произведений:

(7.2)

и является симметричной функцией относительно перестановок любых частиц.

Для системы N фермионов волновая функция должна изменять знак при перестановке любых двух частиц. Поэтому она может быть представлена в виде определителя:

. (7.3)

Из (7.3) следует, что если среди состояний р₁,...,р_N есть два одинаковых, то две строки определителя будут одинаковыми и волновая функция будет равна нулю. Следовательно, вероятность такого события равна нулю. Таким образом, в системе одинаковых фермионов не могут одновременно находиться в одном и том же состоянии (с одинаковым набором квантовых чисел) две (или более) частицы. Это есть так называемый принцип Паули.

Из принципа Паули следует существование чисто квантового взаимодействия, так называемого обменного взаимодействия. Пусть каким-то образом производится сближение двух частиц в одном квантовом состоянии. Поскольку принцип Паули запрещает нахождение в одном месте таких частиц, то возникает их отталкивание. Природа этого взаимодействия выясняется в квантовой электродинамике и состоит в обмене виртуальными фотонами. Обменное взаимодействие может приводить не только к отталкиванию, но и к притяжению частиц. Например, обмен -мезонами между нуклонами в атомном ядре является причиной ядерных короткодействующих сил, а притяжение электронов в кристаллической решётке за счёт обмена фононами, является причиной возникновения сверхпроводимости.