Лекция №3

ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ

Одним из основных принципов квантовой механики является принцип неопределенности, который устанавливает принципиальную невозможность одновременного точного измерения координаты и импульса частицы или энергии и момента времени.

Действительно, как было показано в Лекции 1, правильное описание свободного движения частицы дается не функцией Де Бройля, а волновым пакетом, то есть суммой близких по значению импульса волн Де Бройля. При этом приближенно можно считать, что область локализации частицы Δх и область наиболее вероятных значений импульса Δр на основании (1.18) связаны соотношением

, (3.1)

называемым соотношением неопределенностей для координаты и импульса частицы.

Физический смысл соотношения (3.1), являющийся содержанием принципа неопределенности Гейзенберга, состоит в том, что у квантовой частицы не могут быть одновременно точно измерены координата и импульс. Так, при более точном измерении координаты величина Δх уменьшается, но тогда должна увеличиваться ошибка измерения импульса Δр , и наоборот. В силу малой величины h это справедливо только для квантовых частиц, локализованных в области атомных размеров. Для классических частиц, имеющих макроскопические размеры, можно считать h = 0, тогда из (3.1) следует

,

что означает возможность одновременного точного измерения координаты и импульса. Предельный переход h → 0 в квантовомеханических формулах называется переходом в квазиклассическое приближение.

Отражением глубокой связи между физикой и математикой, как показал Э. Ферми, является возможность формального получения предельной формулировки принципа неопределенности из свойств интегрального преобразования Фурье, связывающего координатное пространство и обратное k-пространство (или, с учетом формулы р=ћk, импульсное пространство).

Предположим, что частица имеет точно определенное значение координаты х=х₀. Тогда ее волновая функция, являющаяся собственной функцией оператора координаты с непрерывным собственным значением х₀, т.е.

имеет вид -функции Дирака, т.е.

.

Представим рассматриваемую волновую функцию в виде интеграла Фурье в k- и р- пространствах:

где ² – плотность вероятности того, что частица имеет импульс р. С помощью обратного преобразования Фурье найдем

.

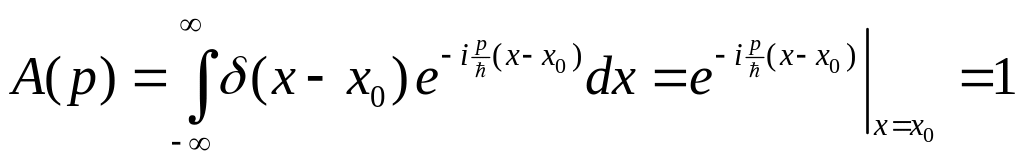Это означает, что частица, у которой точно известна координата, с одинаковой вероятностью может иметь любое значение импульса от – до .

Легко доказать, что верно и обратное утверждение, т.е. частица, у которой точно известен импульс, может с равной вероятностью иметь любую координату от – до . Таким образом, из формальных соображений получена формулировка принципа неопределенности в предельном случае.

Соотношения неопределенностей для конечных Δх и Δр можно получить также, из следующих простых физических соображений. Проварьируем формулу Де Бройля p=ħk (запишем ее в конечных приращениях):

δp=ħδk=ħδ(2π/)= –ħ (2π/²) δ.

Учитывая, что неопределенность длины волны Де Бройля δ≈δх, где δх – неопределенность координаты частицы, а также то, что для квантового объекта размеры, меньшие длины волны Де Бройля, не имеют смысла и, следовательно, δ≈δх≈, получим

|δp| ≈ ħ2π/|δx|

или, что совпадает с (3.1),

|δp| |δx|≈ h .

Это соотношение не противоречит более строгому соотношению, полученному впервые В.Гейзенбергом:

|δp||δx|≥ ħ/2 . (3.1)

Проварьируем теперь соотношение Планка E=h

δE=hδ= hδ(1/T)= h(1/T²)δT.

Полагая, что в течение времени Т происходит переход между энергетическими состояниями квантовой системы, можно считать неопределенность измерения этого времени δT ≈ Т. Тогда получим

|δE| ≈ h |1/δT|

или

|δE| |δT| ≈ h. (3.2)

то есть невозможно одновременно измерить энергию системы и временной интервал самого измерения. Более строгий вывод, проведенный Гейзенбергом, даёт неравенство:

|δE| |δT| ≥ħ . (3.2)

Одновременно измеримыми величинами являются, например, импульс и энергия, действительно

Невозможность одновременного измерения некоторых физических величин в квантовой механике требует формального описания.

Определение

Физические величины F и G одновременно измеримы, если соответствующие операторы и обладают общей системой собственных функций.

В принятых обозначениях, рассматривая для простоты только дискретный спектр, это определение означает:

.

Определение

Коммутатором операторов двух физических величин называется оператор

.

Теорема

Для того, чтобы физические величины F и G были одновременно измеримы, необходимо и достаточно, чтобы коммутатор их операторов был равен нулю:

, (3.3)

или, как еще принято говорить, чтобы операторы и коммутировали:

. (3.4)

Доказательство

Пусть физические величины F и G одновременно измеримы, следовательно, они имеют общий полный базис собственных функций . Тогда любую волновую функцию можно представить в виде

.

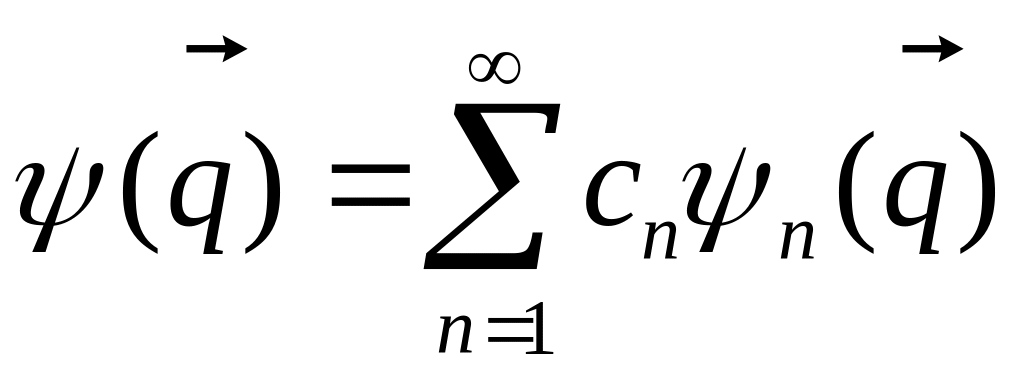Подействуем на произведением операторов:

.

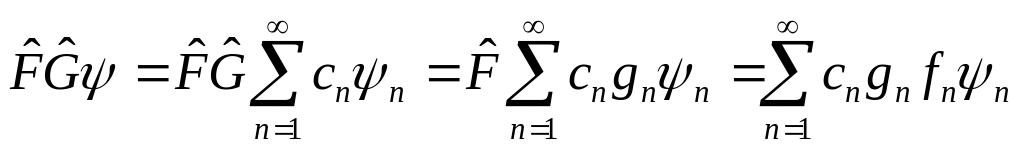
Из полученных равенств следует, что , то есть необходимое условие теоремы доказано.

Докажем условие достаточности, ограничившись невырожденным спектром. Пусть операторы и коммутируют и оператор имеет систему собственных функций {_n}, то есть

.

Пусть действие оператора на функции _n дает некоторую функцию _n , то есть

.

Подействуем на _n оператором :

.

Таким образом, _n также является собственной функцией оператора _{, то есть тоже образует полный базис. Но в силу единственности базиса (невырожденности спектра)} _n может отличаться от _n только на некоторую константу, то есть

.

Тогда

,

следовательно, операторы и _{имеют общую систему собственных функций. Теорема доказана.}

Для примера вычислим коммутатор операторов импульса и координаты. Пусть

,

тогда

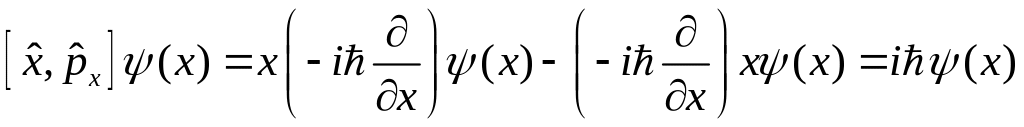, (3.5)

что соответствует ранее полученному результату, состоящему в том, что координата и импульс не могут быть измерены одновременно.