
- •22 Кафедра математического анализа
- •Глава 1. Дифференциальные уравнения
- •§1 Дифференциальные уравнения первого порядка
- •Уравнение вида
- •§2. Дифференциальные уравнения высших порядков. Основные понятия
- •§3. Уравнения второго порядка, допускающие понижение порядка
- •§4. Линейные однородные дифференциальные уравнения второго порядка
- •§ 5. Линейные неоднородные дифференциальные уравнения второго порядка
- •§6. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •§7. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Задания для самостоятельного решения
§2. Дифференциальные уравнения высших порядков. Основные понятия
Уравнение вида
 ,
,
где
- независимая переменная;
- искомая функция;
 - ее производные, называется дифференциальным
уравнением n–го
порядка.
- ее производные, называется дифференциальным
уравнением n–го
порядка.
Обычно изучают уравнения, которые могут быть записаны в виде, разрешенном относительно старшей производной
|
(17) |
Решением
уравнения (17)
называется функция
 ,
,
 ,
которая при подстановке в уравнение
обращает его в тождество. График решения
называется интегральной
кривой.
,
которая при подстановке в уравнение
обращает его в тождество. График решения
называется интегральной
кривой.
Теорема
(Коши).
Если функция
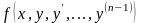 и ее частные производные
и ее частные производные
 ,…,
,…, определены и непрерывны в некоторой
области
пространства переменных
определены и непрерывны в некоторой
области
пространства переменных то какова бы ни была внутренняя точка
то какова бы ни была внутренняя точка
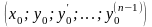 области
,
в некоторой окрестности точки
области
,
в некоторой окрестности точки
 существует единственное решение
уравнения
существует единственное решение
уравнения
 ,
удовлетворяющее условиям
,
удовлетворяющее условиям
|
(18) |
Условия (18) называют начальными условиями решения.
Как и для уравнения первого порядка, задачу отыскания решения по заданным начальным условиям называют задачей Коши.
Функция
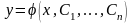 ,
зависящая от
и n
произвольных постоянных
,…,
,
зависящая от
и n
произвольных постоянных
,…, ,
называется общим
решением уравнения (17)
в некоторой области
,
если она является решением уравнения
(17) при любых значениях постоянных
,…,
и если при любых начальных условиях
(18) существуют единственные значения
постоянных
,
называется общим
решением уравнения (17)
в некоторой области
,
если она является решением уравнения
(17) при любых значениях постоянных
,…,
и если при любых начальных условиях
(18) существуют единственные значения
постоянных
 ,…,
,…, такие, что функция
такие, что функция
 удовлетворяет данным начальным условиям.
удовлетворяет данным начальным условиям.
Любая функция , получающаяся из общего решения уравнения (17) при определенных значениях постоянных ,…, , называется частным решением.
Контрольные вопросы:
Дайте определение дифференциального уравнения n-го порядка.
Что называется решением дифференциального уравнения n-го порядка?
Дайте определение общего решения дифференциального уравнения n-го порядка.
Что называется частным решением дифференциального уравнения n-го порядка?
Что называется задачей Коши?
§3. Уравнения второго порядка, допускающие понижение порядка
Уравнение вида
|
(19) |
называется дифференциальным уравнением второго порядка, разрешенным относительно производной.
Рассмотрим три частных случая, когда решение уравнения (19) с помощью замены переменной сводится к решению уравнения первого порядка. Такое преобразование уравнения (19) называется понижением порядка.
1)
Уравнение
вида
 .
Уравнение
не содержит
и
.
Введем новую функцию
.
Уравнение
не содержит
и
.
Введем новую функцию
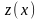 ,
полагая
,
полагая
 .
Тогда
.
Тогда
 ,
и уравнение превращается в уравнение
первого порядка:
,
и уравнение превращается в уравнение
первого порядка:
 с искомой функцией
.
Решая его, находим:
с искомой функцией
.
Решая его, находим:
 .
Так как
,
то
.
Так как
,
то
 .
.
Отсюда, интегрируя еще раз, получаем искомое решение:
 ,
,
где и - произвольные постоянные.
Пример
1.
Найти общее решение уравнения
 .
.
Полагая
,
получаем уравнение первого порядка
 .
Интегрируя его, найдем
.
Интегрируя его, найдем
 .
Заменяя
на
и интегрируя еще раз, находим искомое
общее решение:
.
Заменяя
на
и интегрируя еще раз, находим искомое
общее решение:
 .
.
2)
Уравнение
вида
 .
Уравнение не содержит
.
Положим, как и в предыдущем случае,
;
тогда
,
и уравнение преобразуется в уравнение
первого порядка относительно
:
.
Уравнение не содержит
.
Положим, как и в предыдущем случае,
;
тогда
,
и уравнение преобразуется в уравнение
первого порядка относительно
:
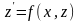 .
Решая его, найдем
.
Решая его, найдем
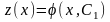 .
Так как
,
то
.
Так как
,
то
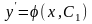 .
Отсюда, интегрируя еще раз, получаем
искомое решение
.
Отсюда, интегрируя еще раз, получаем
искомое решение
 ,
,
где и - произвольные постоянные.
Пример
2.
. Найти общее решение уравнения
 .
.
Полагая
,
получаем линейное уравнение первого
порядка
 .
Решая его, найдем
.
Решая его, найдем
 .
Тогда
.
Тогда
 - искомое решение.
- искомое решение.
3)
Уравнение вида
 .
Уравнение не содержит
.
Вводим новую функцию
.
Уравнение не содержит
.
Вводим новую функцию
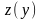 ,
полагая
,
полагая
 .
Тогда
.
Тогда
 .
.
Подставляя
в уравнение выражения для
 ,
получаем уравнение первого порядка
относительно
,
получаем уравнение первого порядка
относительно
 как
функции от
:
как
функции от
:

 .
.
Решая
его, найдем
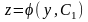 .
Так как
.
Так как
 ,
то
,
то
 .
Отсюда
.
Отсюда
 .
Получено уравнение с разделяющимися
переменными, из которого находим общее
решение данного уравнения:
.
Получено уравнение с разделяющимися
переменными, из которого находим общее
решение данного уравнения:
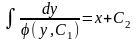 ,
,
где
 - произвольные постоянные.
- произвольные постоянные.
Пример
3.
Найти общее решение уравнения
 .
.
Полагая
 и учитывая, что
и учитывая, что
 ,
получаем
,
получаем
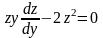 .
Это уравнение первого порядка с
разделяющимися переменными. Приводя
его к виду
.
Это уравнение первого порядка с
разделяющимися переменными. Приводя
его к виду
 и интегрируя, имеем
и интегрируя, имеем
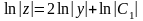 ,
откуда
,
откуда
 .
Учитывая, что
,
находим:
.
Учитывая, что
,
находим: ,
откуда получаем искомое решение
,
откуда получаем искомое решение
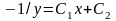 или
или
 .
.
При
сокращении на
было потеряно решение уравнения
 ,
т.е.
,
т.е.

 .
В данном случае оно содержится в общем
решении, так как получается из него при
.
В данном случае оно содержится в общем
решении, так как получается из него при
 (за исключением решения
).
(за исключением решения
).
