Свойства неопределенного интеграла

Вычислению интегралов от тех функций, которые не представлены в приведенной выше таблице интегралов, часто помогают приводимые ниже свойства интегралов.

1. Производная от интеграла равна подынтегральной функции:

.

2. Интеграл от производной равен самой функции (плюс, естественно, ) : .

3. Интеграл от суммы-разности равен сумме-разности интегралов:

4. Постоянный множитель можно выносить за знак интеграла:

Замечание 1. Поскольку есть множество всех первообразных для , то в первом свойстве слева под знаком производной стоит бесконечное множество функций. Поэтому понимать это свойство надо в том смысле, что производная от любой из указанных первообразных равна . Что сразу следует самого определения первообразной. Остальные свойства легко доказываются с помощью правила (*). Докажем, например, по этому правилу последнее свойство интегралов. Для этого нужно взять производную от правой части равенства и убедиться, что получим выражение под интегралом в левой части:

{постоянный множитель при вычислении производной можно выносить за знак производной}= {по первому свойству}= , что как раз является выражением под интегралом в левой части.

Замечание 2. Сравним трудоемкость вычисления интегралов и производных. Для вычисления производных от различных функций тоже (как и для интегралов) сначала была дана таблица производных от основных элементарных функций (степенных, показательных, логарифмических, тригонометрических и т.д.). Затем были даны свойства производных, среди которых присутствовало свойство вынесения постоянного множителя за знак производной, а также формулы для производных от суммы-разности функций, произведения и частного, производных от сложных функций (т.е. функций от функций – например, ). Таким образом, пользуясь таблицей производных и этими свойствами, можно было вычислять производную от функций, заданных сколь угодно сложными формулами, в которых перечисленные элементарные функции умножались бы на числа, складывались, вычитались, умножались и делились между собой, а также брались бы функции от функций. Но таковыми являются все заданные формулами функции, которые могли бы возникнуть в Вашем воображении! Таким образом, для любой функции (представленной сколь угодно сложной формулой) можно (используя таблицу и перечисленные свойства) получить формулу, выражающую производную от данной функции. Конечно, чем объемнее формула, тем дольше придется заниматься получением выражения для производной, но принципиальных проблем для этого нет. Вернемся к вычислению интегралов. Для них тоже есть таблица интегралов от основных элементарных функций и свойства. Однако среди свойств есть только вынесение множителя за знак интеграла и формула интеграла от суммы или разности функций. И нет формул для интеграла произведения или частного функций, а также интеграла от сложной функции! Такие формулы многие студенты сами «придумывают» на контрольных работах и экзамене, за что получают снижение оценки как за грубую ошибку. Таким образом, пока имеется принципиальная возможность вычислять интегралы лишь от таких функций, которые выражаются через основные элементарные функции только с помощью их сложения, вычитания и умножения на числа. Но не умножения, деления и взятия функций от функций! Этот факт значительно усложняет задачу вычисления интегралов, так как многие функции в своей формульной записи содержат именно эти «запрещенные» операции! Именно поэтому вычисление интегралов, в общем случае, намного сложнее вычисления производных! По этой причине при вычислении интегралов от функций, в записи которых есть умножение-деление или сложные функции, пытаются тождественно преобразовать подынтегральное выражение так, чтобы в нем остались только «разрешенные» операции (+, − , умножение на числа). Как именно иногда можно умножение-деление свести к сложению-вычитанию будет видно из приведенных ниже примеров. Но очень часто это сделать невозможно. Для этих случаев в учебниках описывается множество искусственных частных приемов (некоторые из них мы пройдем позднее) , каждый из которых, к сожалению, «срабатывает» только для узкого класса подынтегральных функций своего частного вида. Но даже набор этих приемов помогает вычислить интегралы далеко от всех функций. Есть функции (даже достаточно простого вида), интегралы от которых принципиально не могут быть выражены в виде «обычных» формул (основных элементарных функций, соединенных в формулу перечисленными выше операциями ). Например, если выражается формулой просто (табличный интеграл), то уже чуть усложненный «обычной» формулой не выражается (хотя производную от вычислить совсем несложно благодаря формуле производной от сложной функции или обобщенной таблице производных: ) . И дело не в том, что пока никто не смог найти эту формулу, а в принципиальной невозможности существования такой формулы: нельзя придумать такую формулу (ее попросту не существует!), беря производную от которой получили бы . Таким образом, первообразная от обычной привычной формулой не выражается, а потому не выражается такой формулой и . Такие интегралы называют «неберущимися» или интегралами, которые не выражаются в элементарных функциях. Не следует, однако, думать, что если привычное «формульное» представление интеграла невозможно, то и интеграла нет. Можно считать, что для его выражения просто не хватает запаса привычных формул и их надо расширить, то есть выйти за рамки множества функций, выражающихся через основные элементарные функции с помощью арифметических операций и функций от функций. В науке и её приложениях в технике, экономике и других дисциплинах применяются такого типа функции, которые называются специальными функциями. К специальным функциям относятся и многие «неберущиеся» интегралы от элементарных функций. Вот некоторые такие функции и их названия:

а) − «почти» функция Лапласа б) − интегральный синус в) − интегральный косинус г) − интегральная экспонента д) − интегральный логарифм.

А теперь приведем примеры, в которых можно обойтись перечисленными свойствами интегралов и таблицей интегралов от основных элементарных функций.

Пример 1. Вычислить .

Решение. = {свойство 3} = = = {свойство 4} = = {формулы 3, 2, 1 таблицы интегралов } = = .

Итак, = .

Пример 2. Вычислить .

Решение. = {свойство 3} = = {свойство 4} = = {формула 10 таблицы интегралов и формула 11 при } = . Итак, = .

Если при взятии интеграла использовались только приведенные выше свойства и приведенная выше простая таблица интегралов, то говорят, что интеграл вычислен методом непосредственного интегрирования.

Пример 3. Вычислить интеграл методом непосредственного интегрирования.

Решение. Сложность в том, что подынтегральная функция содержит операцию умножения, а формулы для интеграла от произведения функций нет! Но в этом случае легко избавиться от умножения, раскрыв скобки:

= {заменяем корни дробными степенями} = = {раскрываем скобки под знаком интеграла}= = {свойство 3 и 4 интегралов − интеграл от суммы равен сумме интегралов, а постоянные множители можно выносить за знак интеграла} = = = {формула 3 таблицы интегралов при и } = = .

Итак, = .

Пример 4. Вычислить .

Решение. Здесь под интегралом присутствует деление (на ), но формулы для интеграла от частного двух функций не существует. В этом примере тоже можно деление свести к сложению-вычитанию, деля каждое слагаемое в числителе на знаменатель:

={делим каждое слагаемое в числителе на знаменатель и заменяем корень дробной степенью}=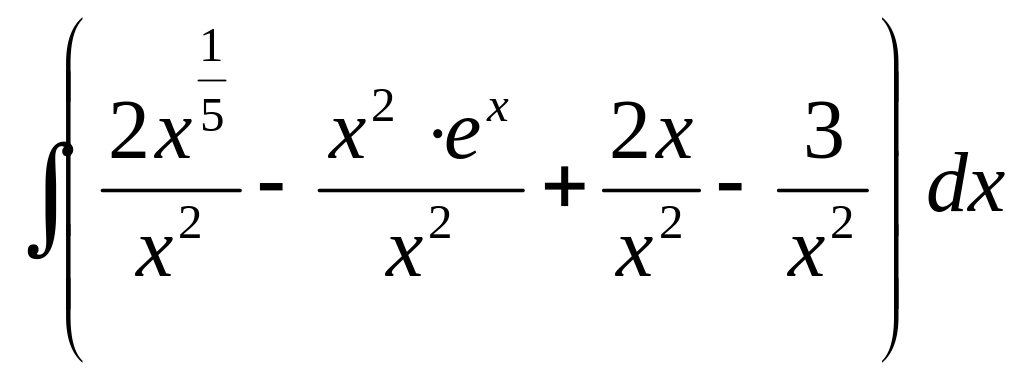 = = = {интеграл от разности равен разности интегралов, числовые множители выносим за интегралы}= = {смотрим таблицу интегралов} = = .

Итак, = .