Частные производные

Особую роль для приложений играет обобщение понятия производной с функции одной переменной на функции двух и более переменных. Для функции двух переменных существует уже 2 типа производных (по количеству независимых переменных и ), которые характеризуют скорость и характер изменения функций по каждой из переменных. Они называются частными производными. Перейдем к точным формулировкам. Пусть функция определена в некоторой окрестности точки (теперь окрестностью точки на координатной плоскости называется множество точек внутри некоторого круга с центром в данной точке). Зафиксируем в этой функции одну из переменных. Сначала зафиксируем , тогда переменная станет уже функцией одного переменного , которую обозначим : . Частной производной по переменной функции в точке называется обычная производная функции одного переменного в точке (если она, конечно, существует). Имеется несколько обозначений частной производной по в точке : , , , . Аналогично, зафиксируем , тогда переменная станет уже функцией одного переменного , которую обозначим . Частной производной по функции в точке называется обычная производная функции в точке (если она, конечно, существует). Обозначения частной производной по у: , , , . Из определения частных производных следует следующее

Правило вычисления частных производных для функции двух переменных.

1. Частная производная по вычисляется по обычным правилам вычисления производных, если переменную (и вообще, любое выражение, не содержащее ) считать постоянным числом.

2. Частная производная по вычисляется по обычным правилам вычисления производных, если переменную (и вообще, любое выражение, не содержащее ) считать постоянным числом.

В связи с изложенной схемой напомним правила вычисления обычных производных, касающиеся чисел: а) производная от числа равна нулю ( ); б) если число является множителем, то постоянный множитель можно выносить за знак производной.

Пример 1. Найти выражения для обеих частных производных функции в произвольной точке . Найти значение частной производной по в точке , т.е. найти .

Решение. Найдем сначала выражение для частной производной по , т.е. . Ясно, что 3 есть число, но так как оно умножается на , то оно является постоянным множителем, а потому по обычным правилам вычисления производной его можно вынести за знак производной. Однако кроме числа 3 есть еще и множитель , который, по приведенному выше правилу вычисления частной производной по , тоже надо считать постоянным числом (в выражении нет иксов!). Поэтому при вычислении частной производной по все выражение можно считать постоянным множителем (при ), а потому может быть вынесено за знак производной. Итак, . По обычным правилам вычисления производной (из простой таблицы производных) : . Окончательно получаем: . Вычислим теперь производную по , вспоминая, что теперь постоянным числом надо считать любое выражение, не содержащее , а в остальном применять обычные правила вычисления производных. После предыдущих комментариев по вычислению уже должна быть понятна следующая цепочка преобразований: . Итак, . Тогда .

Пример 2. Найти частные производные функции . Решение. Найдем выражение для . Вспоминаем, что производная суммы-разности выражений равна той же сумме-разности производных от этих выражений, поэтому . Далее, при вычислении каждой их получившихся производных по учитываем, что выражения, не содержащие , считаются постоянными (числами), а потому они либо выносятся за знак производной (если являются множителями при выражении, которое содержит), либо производная от них равна нулю. Поэтому

. Итак, . Аналогично вычисляем производную по , но теперь числами считаем выражения, не содержащие , а потому снова либо выносим их за знак производной, либо сразу заменяем на 0: .

Пример 3. Найти частные производные функции .

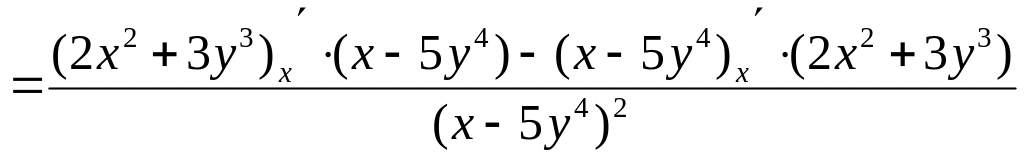Решение. Найдем . Поскольку выражение для функции представляет собой дробь (точнее, отношение двух функций), то вспоминаем соответствующую формулу из правил вычисления обычной производной: . Применяя ее, получаем . Вычислим отдельно производные, присутствующие в числителе полученного выражения: , . Подставляя вычисленные выражения, получаем . Раскрывая скобки в числителе и приводя подобные: . Аналогично вычисляется и производная по : . Далее, , . Подставляя полученные выражения в формулу для производной, окончательно получаем .

Пример 4. Найти частные производные функции .

Решение. Производная по : {применяем формулу для производной от произведения } = . Вычислим отдельно возникшие производные и вставим полученное обратно в формулу: {применяем из обобщенной таблицы производных формулу } , {применяем из обобщенной таблицы производных формулу } {вспоминаем, что при вычислении производной по переменную нужно считать числом (в данном случае – постоянным множителем) и выносить за знак производной}= . Подставляя вычисленные производные в формулу для , получаем . Аналогично для производной по переменной : . Посчитаем возникшие производные: , { - постоянный множитель при взятии производной по } = . Подставляя полученные производные в выражение для , окончательно получим .

Пример 5. Доказать, что функция удовлетворяет условию: . Решение. Для доказательства требуемого мы должны в правую часть данного условия подставить , а в левую часть этого условия вместо частных производных и подставить вычисленные их выражения, а затем убедиться, что получилось тождество. Найдем эти производные: частная производная {производная от произведения } = {выражение не содержит , а потому при вычислении производной по его надо считать числом, производного от которого, как известно, есть 0} . Итак, . Далее, аналогично {переменная при вычислении производной по считается числом (в данном случае это постоянный множитель) – выносится за знак производной } . Итак, . Подставляя полученные производные в левую часть проверяемого условия, получим { вспоминаем, что как раз } , что и требовалось получить.

Пример 6. Найти частную производную по функции .

Решение. Попробуйте теперь понять проводимые преобразования без пояснительных комментариев с моей стороны: = . Окончательно .

Аналогично определяются частные производные для функции трех (и более) переменных Таких производных уже будет 3 типа (по количеству независимых переменных , и ). Частная производная от функции по в точке может обозначаться одним из следующих способов: , , , . Аналогичные обозначения могут быть использованы для частной производной по ( , , , ) и по ( , , , ).

Правило вычисления частных производных для функции трех переменных практически то же самое, что и для функции двух переменных (сравните).

1. Частная производная по вычисляется по обычным правилам вычисления производных, если переменные и (и вообще, любое выражение, не содержащее ) считать постоянным числом.

2. Частная производная по вычисляется по обычным правилам вычисления производных, если переменные и (и вообще, любое выражение, не содержащее ) считать постоянным числом.

3. Частная производная по вычисляется по обычным правилам вычисления производных, если переменные и (и вообще, любое выражение, не содержащее ) считать постоянным числом.

Аналогично формулируется правило вычисления частных производных для функции любого числа переменных.

Пример 6. Найти частные производные функции . Решение. Используем сформулированное правило: {в первом слагаемом выражение не содержит , а потому при вычислении производной по оно считается постоянным множителем при и выносится за знак производной} {т.к. } . Далее, {в первом слагаемом выражение не содержит , а потому при вычислении производной по оно считается постоянным множителем при и выносится за знак производной} . Наконец, {в первом слагаемом выражение не содержит , а потому при вычислении производной по оно считается постоянным множителем при и выносится за знак производной; выражение под знаком производной во втором слагаемом не содержит , а потому считается числом при вычислении производной по } .