Интегрирование некоторых иррациональных выражений

Рассмотрим в первую очередь интегрирование выражений, в которых аргумент входит только под знаком показательной функции (для простоты – экспоненты). Это интегралы вида . Здесь под понимается любая формула, в которую аргумент входит только под знаком экспоненты (где − некоторое число). В этом случае рекомендуется замена переменной в интеграле по формуле (так новая переменная связана с исходной переменной ). Найдем дифференциал новой переменной : . Учитывая, что , получаем , откуда . Поэтому при замене переменной в интеграле вида для указанной замены выражение везде заменяется на , а заменяется на . Оформляется это следующей записью:

(1) .

После вычисления интеграла в правой части (1) следует в ответе вернуться к исходной переменной , заменяя обратно на .

Приведем пример.

Пример 1. Вычислить .

Решение. Это интеграл вида при , поскольку под интегралом входит только в выражение вида (то, что встречается и выражение не мешает такому выводу, так как ). Поэтому используем замену переменной (1) (при ) : .

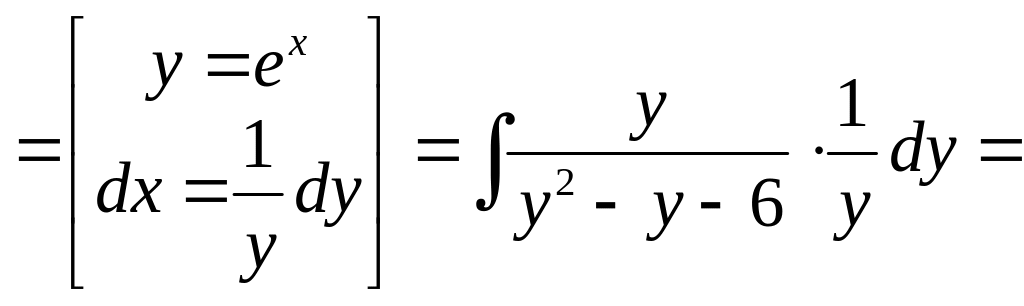
По переменной получился интеграл от рациональной функции . Воспользуемся тем, что в предыдущем параграфе мы уже вычисляли интеграл от такой функции (только переменная была не , а привычная ) и получили такой ответ: . Заменяя обозначение переменной с на нужное в данном примере , получаем:

.

Возвращаясь к исходной переменной , заменяем в полученном ответе на , получаем окончательный ответ:

.

Рассмотрим теперь интегрирование некоторых выражений, в которых встречаются корни любой степени от линейных по выражений. Это интегралы вида . Здесь под понимается любая формула, в которую аргумент может входить и сам по себе, но обязательно входит и в комбинацию вида так и в комбинации вида (где и − некоторые числа). В этих случаях новая переменная вводится по формуле . Выразим обратно старую переменную через новую , для чего возведем обе части последнего равенства в степень : . Отсюда . Найдем из этой формулы дифференциал переменной , считая ее функцией от : . Таким образом, при замене переменной по формуле нужно в подынтегральном выражении везде заменить на , выражение везде заменить на , а заменить на .

Оформляется это следующей записью:

(2) .

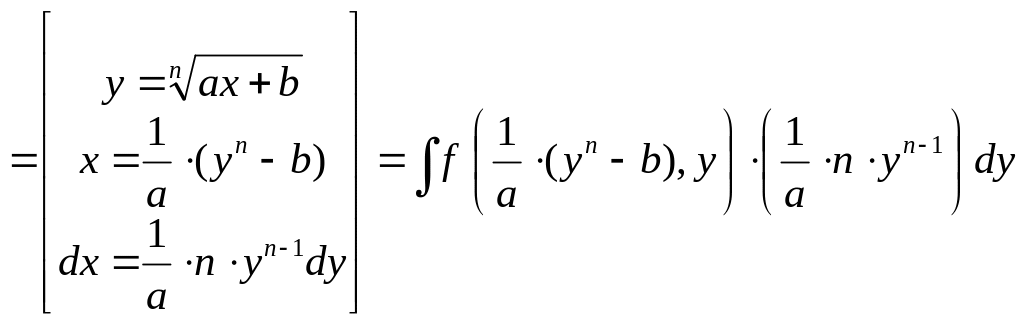После вычисления интеграла в правой части (2) следует в ответе вернуться к исходной переменной , заменяя обратно на .

Приведем пример.

Пример 2. Вычислить .

Решение. Это интеграл изучаемого вида , так как в подынтегральное выражение входит квадратный корень . По приведенной в таких случаях рекомендации применяем метод замены переменной, вводя новую переменную интегрирования по формуле . Выразим обратно старую переменную через новую , возводя обе части равенства в квадрат: . Отсюда . Выразим дифференциал через дифференциал новой переменной : , т.е. . Теперь для получения интеграла по новой переменной в подынтегральном выражении заменяем на , выражение заменяем на , а на : 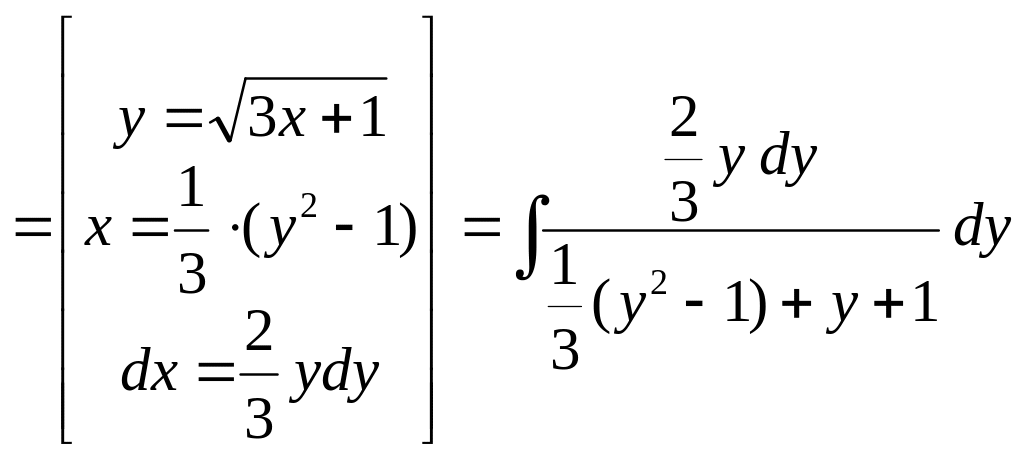= { для упрощения умножим числитель и знаменатель дроби на 3} = . Таким образом, мы пришли к необходимости вычисления интеграла . Это интеграл от рациональной функции (алгебраической дроби), поэтому его вычисление проводим по схеме, предложенной в предыдущем параграфе (с учетом того, что переменная теперь имеет обозначение не , а ) .

1) Для разложения на множители квадратного трехчлена в знаменателе приравниваем его нулю и находим корни: , , . Поэтому знаменатель так раскладывается на множители: .

2) В соответствии с полученным разложением на множители знаменателя записываем интегрируемую дробь в виде суммы простейших дробей с неопределенными коэффициентами и : .

3) Находим числовые значения неопределенных коэффициентов и . Приведем сумму дробей к общему знаменателю:

.

Таким образом, . Приравнивая числители этих дробей, получим, что для всех должно выполняться равенство : . Подставим в это равенство поочередно и (те значения , при которых одно из слагаемых слева обращается в 0):

а) при получаем , т.е. , откуда .

б) при : , т.е. .

4) Итак, и , поэтому . Поэтому получаем такой ответ в новой переменной :

.

Остается сделать в полученном ответе переход к старой переменной , заменяя на , после чего получается окончательный ответ для исходного интеграла:

.

Рассмотрим теперь интегрирование некоторых выражений, в которых встречается квадратные корни типа . Это интегралы вида . В этих случаях опять применяется замена переменной, причем старая переменная так выражается через новую переменную : . При такой замене переменной переходит в , а . Таким образом,

(3) .

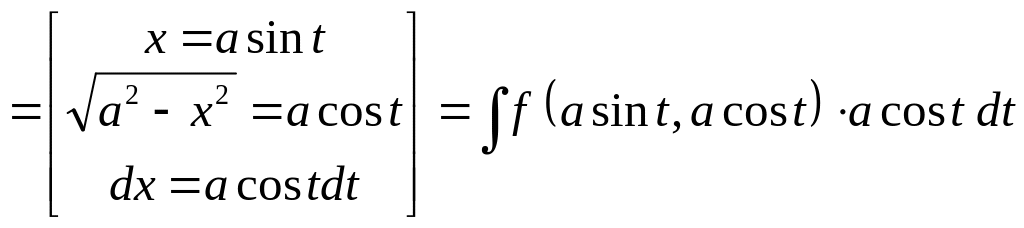После вычисления интеграла по новой переменной в правой части, необходимо вернуться снова к исходной переменной . Если , то , поэтому . Таким образом, после вычисления полученного интеграла по переменной необходимо в ответе заменить на .

Рассмотрим пример.

Пример 3. Вычислить .

Решение. Это интеграл изучаемого вида , так как в подынтегральное выражение входит , а это как раз при . Делаем рекомендуемую в (3) замену переменных :

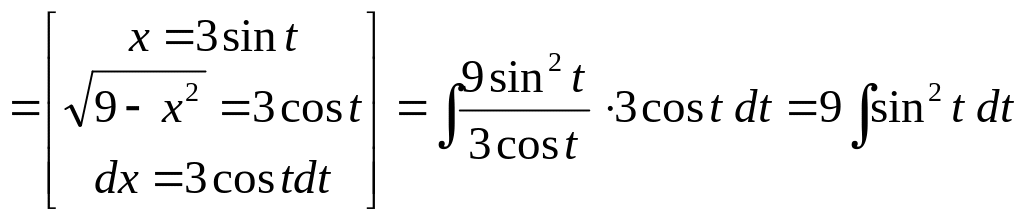= { используем формулу понижения степени }= . Возвращаясь к исходной переменной по формуле , окончательно получаем:

.

96