Интегрирование выражений, содержащих логарифмы
Если
логарифм (или его натуральная степень)
под интегралом умножается на некоторую
степень
,
то интеграл вычисляется методом
интегрирования по частям, что разобрано
выше. Рассмотрим теперь интегрирование
выражений, в которых аргумент
в числителе входит только
под знаком логарифма (для простоты –
натурального). Это интегралы вида
. Здесь под
понимается любая формула, в которую
аргумент
входит только в комбинации
(где
и
− некоторые числа), причем вся эта
формула обязательно под интегралом
должна делиться на
(это деление может быть и представлено
и умножением на
). В этом случае рекомендуется замена
переменной в интеграле по формуле
(так новая переменная
связана с исходной переменной
).
Найдем дифференциал
:
.
Таким образом,
,
откуда
.
Поэтому при замене переменной в интеграле
вида
(который может быть записан и в виде
) при указанной замене
выражение
везде заменяется на
,
а
заменяется на
.
Оформляется это следующей записью:
(1)
.
Отметим,
что в часто встречающемся частном случае
интеграла вида
(т.е. при
) формула (1) переходит в более простую:
(2)
.
Приведем примеры на описанный прием вычисления интегралов.
Пример 1.
Вычислить
.
Решение. В числителе
входит только в комбинации
и есть
в знаменателе, поэтому используем замену
переменной (1) (при
) :
{
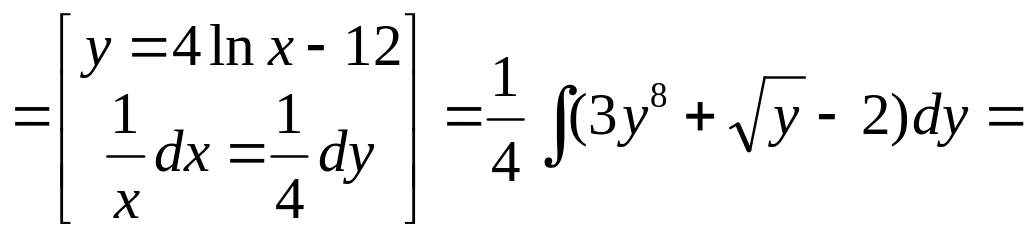
остались интегралы из простой таблицы,
только переменная интегрирования теперь
обозначена не
,
а
, поэтому и ответ будет с этой переменной}
{
возвращаемся в полученном ответе к
старой переменной
, учитывая, что
}=
.
Окончательно:
.
Замечание.
В конце ответа можно было бы заменить
одной буквой
− от этого все множество соответствующих
первообразных не изменилось бы.
Пример 2.
Вычислить
.
Решение. В числителе
входит только под знаком логарифма есть
в знаменателе, поэтому используем замену
переменной (2) :
{
первый интеграл – табличный, а для
вычисления второго воспользуемся
результатом примера 2 предыдущего
параграфа
,
заменив, естественно,
на
}=
={
возвращаемся в полученном ответе к
старой переменной
, учитывая, что
}
. Итак,
.
Интегрирование выражений, содержащих тригонометрические функции
Рассмотрим
интегрирование некоторых типов выражений,
в которых аргумент
входит только под знаком тригонометрических
функций. Прежде всего рассмотрим
интегралы вида
и
. В интеграле
под
понимается любая формула, в которую
аргумент
входит только в комбинацию
(где
− некоторое число), причем вся эта
формула обязательно под интегралом
должна умножаться на
.
Аналогично, в интеграле
под
понимается любая формула, в которую
аргумент
входит только в комбинацию
,
но вся эта формула под интегралом
умножается на
.
Для интегралов вида
рекомендуется замена переменной
.
Найдем дифференциал новой переменной:
,
откуда
.
Отсюда следует, что при переходе в
интеграле
к новой переменной
(со связью переменных
)
следует в формуле
везде
заменить на
,
а оставшееся выражение
заменить на
.
Аналогично, легко показать, что при
переходе в интеграле
к новой переменной
(со связью
)
следует в формуле
везде
заменить на
,
а оставшееся выражение
заменить на
.
Оформляется это следующей записью:
(1)
.
(2)
.
Приведем примеры на вычисления интегралов указанных типов.
Пример 1.
Вычислить
.
Решение. Это
интеграл типа (1) (при
),
поскольку
входит только в комбинацию
и есть множитель
перед
.
Тогда по формуле (1) :
{ возвращаемся к старой переменной
,
учитывая, что
}
=
Окончательно:
Пример 2.
Вычислить
.
Решение. Это
интеграл типа (2) (при
),
поскольку
входит только в комбинацию
и есть множитель
перед
.
По формуле (2) :
{для
удобства вносим знак « − » в скобки
подынтегрального выражения, меняя знаки
в них}=
=
{возвращаемся
к старой переменной
}
.
Итак,
.
Пример 3.
Вычислить
.
Решение. Это
интеграл типа (1) при
,
поскольку
входит только в комбинацию
и есть множитель
перед
.
По формуле (1) :
.
Окончательно:
.
Пример 4.
Вычислить
.
Решение. Формально
подынтегральное выражение не позволяет
данный интеграл отнести к типу (1) или
(2). Вот если бы степень синуса или степень
косинуса была бы равной 1,
то интеграл бы оказался одного из этих
типов. Для того, чтобы привести интеграл
к нужному типу, воспользуемся основным
тригонометрическим тождеством
,
которое позволяет выразить квадрат
одной из тригонометрических функций
через другую. Подынтегральная функция:
.
Поэтому
.
Теперь видно, что это интеграл вида (1),
причем
,
а перед
стоит
.
Тогда по формуле (1):
.
Таким образом,
.
Рассмотрим теперь
интегралы
от произведений тригонометрических
функций вида
.
Для избавления от произведения под
интегралом и превращения его в
сумму-разность используются следующие
формулы тригонометрии:
,
,
.
Пример 5.
Вычислить
.
Решение. Используем
последнюю формулу произведения синуса
и косинуса:
=
={пользуемся
нечетностью синуса:
}
=
.
Окончательно получаем:
.
Рассмотрим теперь
вычисление
интегралов от четных степеней
тригонометрических функций.
Для их вычисления используют следующие
тригонометрические формулы понижения
степени:
и
.
Пример 6.
Вычислить
.
Решение. Используем
формулу понижения степени
:
.
Итак,
.
Пример 7.
Вычислить
.
Решение. Используем
формулу понижения степени
,
представив четвертую степень как
«квадрат в квадрате»:
{раскрываем
квадрат суммы}
{к
последнему интегралу снова применяем
формулу понижения степени}=
.
Окончательно :
.