
- •Оглавление
- •Раздел VII. Функции нескольких переменных 4
- •Раздел VIII. Неопределенный интеграл 54
- •Раздел VII. Функции нескольких переменных Основные понятия
- •Частные производные
- •Частные производные высших порядков
- •Производная по направлению и градиент
- •Экстремумы функций двух переменных
- •Раздел VIII. Неопределенный интеграл Основные понятия
- •Свойства неопределенного интеграла
- •Внесение под знак дифференциала и обобщенная таблица интегралов
- •Замена переменной в неопределенном интеграле
- •Интегрирование по частям
- •Интегрирование выражений, содержащих логарифмы
- •Интегрирование выражений, содержащих тригонометрические функции
- •Интегрирование рациональных функций
- •Интегрирование некоторых иррациональных выражений
Интегрирование по частям
Это
второй из наиболее общих специальных
методов вычисления интегралов. Пусть
функции
![]() и
и
![]() дифференцируемы (т.е. имеют производную)
на рассматриваемом интервале изменения
.
Тогда верно равенство
дифференцируемы (т.е. имеют производную)
на рассматриваемом интервале изменения
.
Тогда верно равенство
![]()
Данная
формула и называется формулой
интегрирования по частям,
а доказывается она легко применением
правила (*) и формулы производной
произведения. Эту формулу можно записать
и в более компактной форме, если заметить,
что по определению дифференциала функции
![]() ,
а
,
а
![]() .
Делая соответствующую подстановку в
написанной формуле и опуская для
краткости обозначение аргумента х
у функций, получим
.
Делая соответствующую подстановку в
написанной формуле и опуская для
краткости обозначение аргумента х
у функций, получим
![]()
Именно в такой форме формула записана во многих учебниках. Но, думается, удобнее ее применять в первоначальной форме, тоже опустив для краткости обозначение аргумента х у функций :
(1)
![]() .
.
Доказательство
формулы (1) достаточно простое. По правилу
(*) (в параграфе «Основные понятия») для
того, чтобы убедиться, что правая часть
формулы (1) действительно представляет
собой значение интеграла в левой части,
надо взять производную от правой части
(1) и получить при этом подынтегральную
функцию
![]() в интеграле слева. Проделаем это:
в интеграле слева. Проделаем это:
![]() ={используем
формулу производной произведения и
свойство 1 неопределенного интеграла
в параграфе «Свойства неопределенного
интеграла» о том, что производная от
интеграла равна подынтегральной
функции}
={используем
формулу производной произведения и
свойство 1 неопределенного интеграла
в параграфе «Свойства неопределенного
интеграла» о том, что производная от
интеграла равна подынтегральной
функции}![]() ,
что и требовалось.
,
что и требовалось.
Формула
интегрирования по частям (как и замены
переменной) сводит вычисление одного
интеграла (в левой части) к вычислению
другого интеграла (в правой части).
Поэтому ее целесообразно применять
только тогда, когда второй интеграл
оказывается более простым для вычисления,
чем первый. Формула интегрирования по
частям применяется для интегрирования
произведения функций разного типа
(например, тригонометрической и степенной,
тригонометрической и показательной,
степенной и показательной (логарифмической)
и т.д. ). Далее будут даны более конкретные
рекомендации. Для применения формулы
(1) интегрирования по частям надо разбить
подынтегральную функцию на 2 сомножителя,
взяв один из них за u,
а другой за v′
(причем очень
важно правильно выбрать, что за что
брать – от этого зависит успех применения
формулы). Потом
по этим данным нужно найти u′
и v
для подстановки их в правую часть формулы
(1). Выражение для u′
получается из u
обычным дифференцированием, а выражение
для v
из v′
(как и всякое восстановление функции
по известной ее производной) получается
интегрированием:
![]() (см. свойство 2 интеграла), причем при
вычислении этого интеграла достаточно
найти только одну первообразную, поэтому
«+С» потом можно не писать.
(см. свойство 2 интеграла), причем при
вычислении этого интеграла достаточно
найти только одну первообразную, поэтому
«+С» потом можно не писать.
Пример 1.
Вычислить
![]() интегрированием по частям (впрочем,
по-другому и не получится).
интегрированием по частям (впрочем,
по-другому и не получится).
Решение. Применяем
формулу (1), взяв
за
![]() ,
а
,
а
![]() за
за
![]() :
:
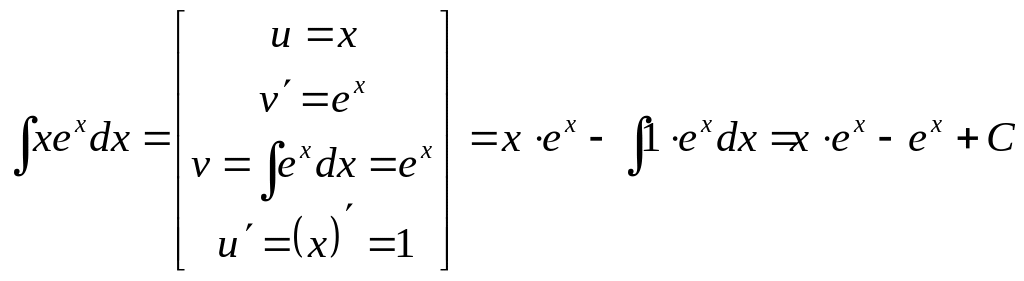
Между большими квадратными скобками записывается комментарий, описывающий подготовку к применению формулы (1) интегрирования по частям. Содержимое комментария, в принципе, не является частью формулы и записывается для удобства.
Дадим теперь обещанные конкретные рекомендации по применению этой формулы. Чаще всего формула интегрирования по частям (1) применяется для вычисления интегралов следующих типов (одновременно даны рекомендации − что брать за , а что за ) :
1.
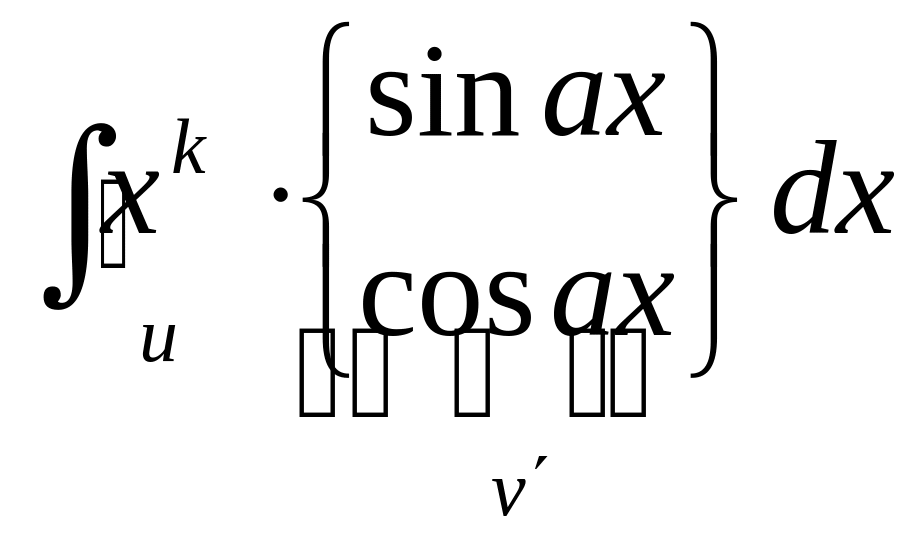 2.
2.
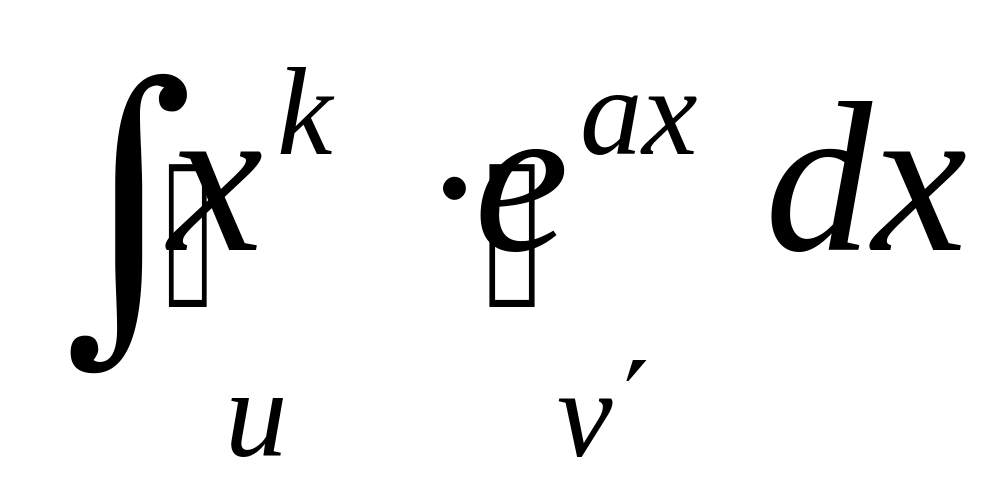 3.
3.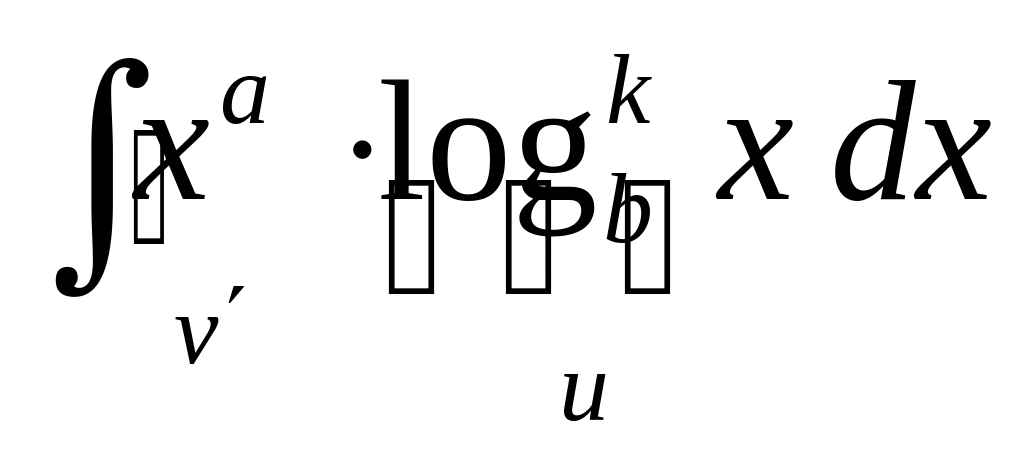 4.
4.
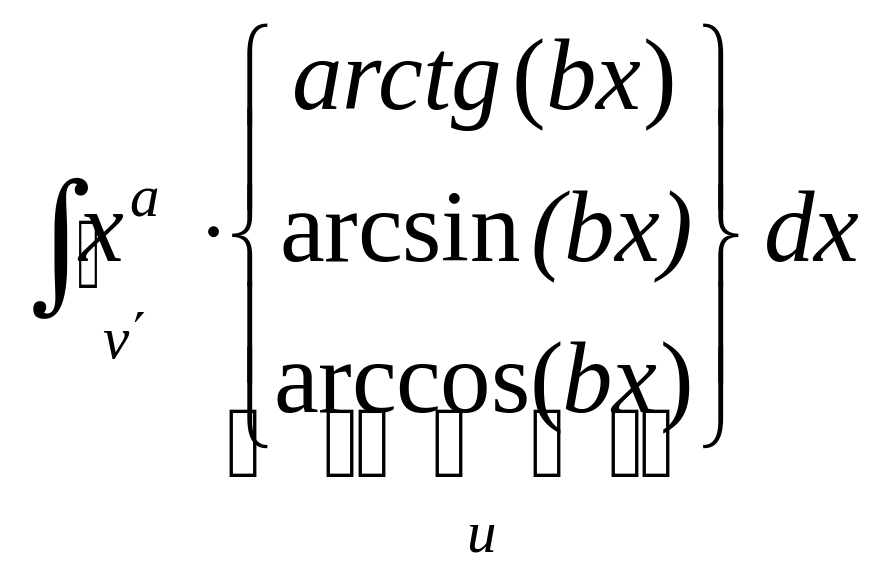 .
.
В написанных интегралах − неотрицательное целое число, a и b – произвольные числа (в основании логарифма, естественно, b>0 и b ≠ 1). Причем там, где стоит в показателе степени, интегрирование по частям приходится проводить раз, пока не получится интеграл из таблицы интегралов.
Пример 2.
Вычислить
![]() .
.
Решение. Это
интеграл первого из перечисленных выше
типов при
![]() и
,
поэтому перед применением формулы (1)
делаем рекомендуемый выбор функций
и
:
и
,
поэтому перед применением формулы (1)
делаем рекомендуемый выбор функций
и
:
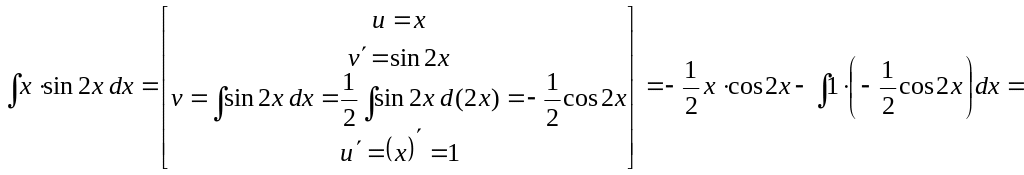
![]()
Пример 3.
Вычислить
![]() .
.
Решение. В данном
примере под интегралом только одна
функция, поэтому казалось бы формулу
интегрирования по частям применять
нельзя. Однако всегда вторым множителем
можно сделать единицу:
![]() .
Теперь видно, что это интеграл третьего
типа при
.
Теперь видно, что это интеграл третьего
типа при
![]() (так как
(так как
![]() ),
),
![]() и
.
Применяем формулу (1):
и
.
Применяем формулу (1):
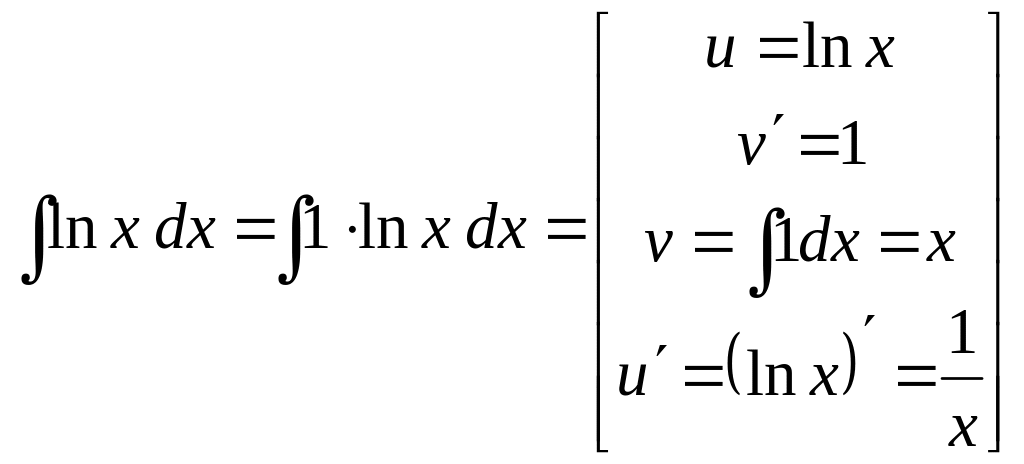 =
=
![]() .
.
Пример 4.
Вычислить
![]() .
.
Решение. Поскольку
![]() ,
то это снова интеграл третьего типа при
,
то это снова интеграл третьего типа при
![]() ,
и
:
,
и
:
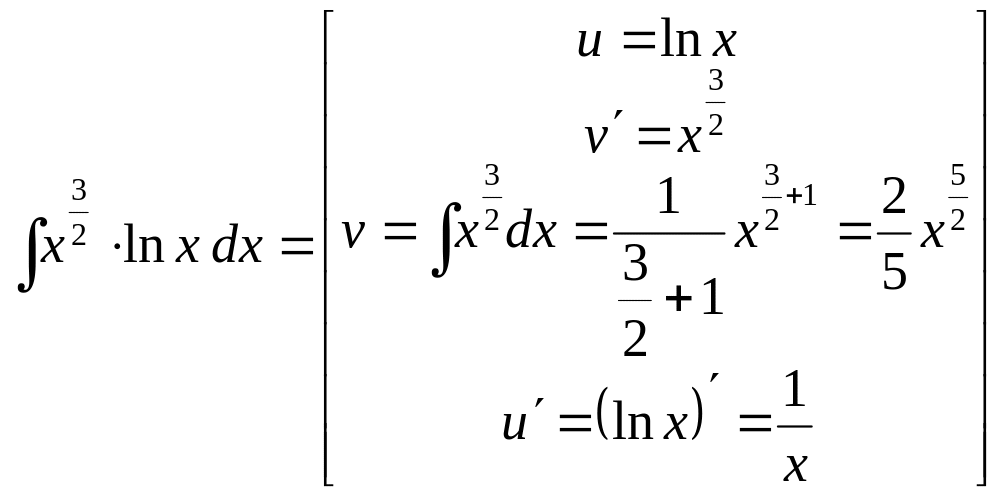
![]()
![]() .
.
Пример 5.
Вычислить
![]() .
.
Решение. Это
интеграл второго типа при
![]() (а потому формулу интегрирования по
частям придется применять 2 раза) и
:
(а потому формулу интегрирования по
частям придется применять 2 раза) и
:
(2)
![]()
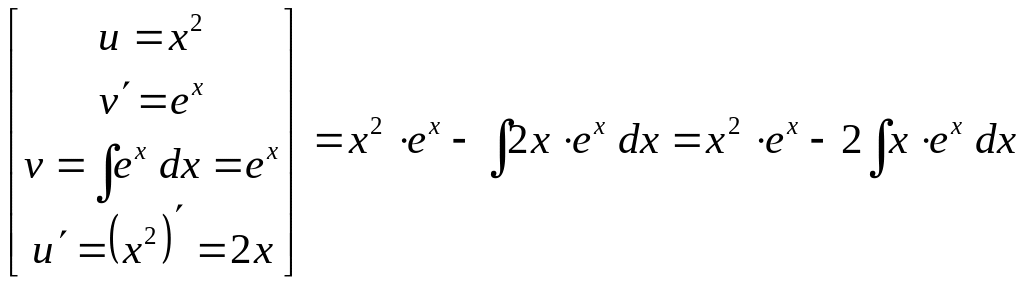 .
.
Справа в (2) опять
получился интеграл того же типа, но при
.
Вычислим его снова по формуле интегрирования
по частям и подставим в (2) :
![]()
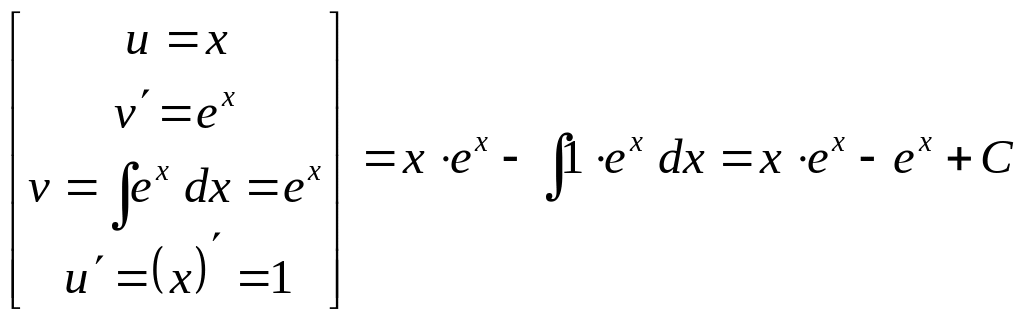 .
Подставляя в (2), окончательно получим
:
.
Подставляя в (2), окончательно получим
:
![]() .
.
Пример 6.
Вычислить
![]() .
.
Решение. Это
интеграл четвертого типа из тех, которые
выше рекомендовано вычислять методом
интегрирования по частям (![]() ):
):
![]()
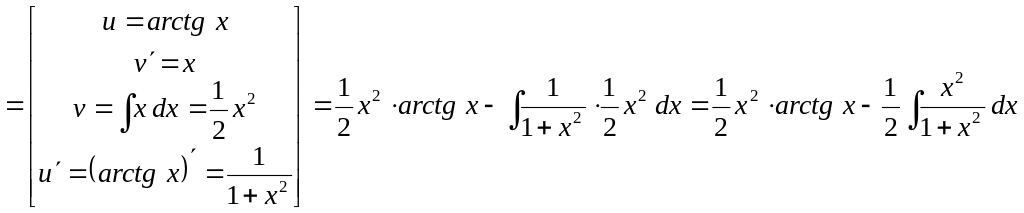 .
Вычислим последний интеграл, приведя
его к табличным:
.
Вычислим последний интеграл, приведя
его к табличным:
![]() =
=![]() .
Подставляя полученное значение интеграла
в предыдущее выражение, окончательно
получим:
.
Подставляя полученное значение интеграла
в предыдущее выражение, окончательно
получим:
![]() .
.
Рассмотрим теперь некоторые специальные приемы для интегрирования некоторых классов функций.
