Непрерывные функции

Н епрерывность − понятие геометрическое. Можно говорить о непрерывной линии, поверхности и т.п. . Когда вводится понятие непрерывности функции, то имеют в виду не вид формулы , которой задается функция, а форму ее графика, который действительно имеет вид некоторой линии на координатной плоскости . Рассмотрим (на рисунке) возможный вид графика некоторой функции . Видно, что график во всех своих точках имеет вид непрерывной линии, кроме одной точки, в которой линия графика терпит разрыв. Это происходит в точке с -координатой, равной , но не происходит в точке с -координатой, равной, например, . Поэтому интуитивно хочется назвать точку (число) точкой разрыва функции, а точку (да и все остальные точки, кроме ) точками непрерывности функции. Но для того, чтобы дать строгие определения, необходимо опираться не на график функции, который в общем случае построить достаточно непросто, а на выражение (формулу) , которым задана функция. Попробуем выяснить, чем отличается поведение функции в точке (которую естественно было бы назвать точкой непрерывности функции ) от ее поведения в точке (которая в дальнейшем получит название точки разрыва этой функции). Выясним (ориентируясь на представленный график функции), чему равен левый предел функции в точке . Для этого представим себе набор точек (чисел) , приближающихся к слева (со стороны чисел, меньших ) и по представленному графику попробуем определить, к какому числу приближаются значения функции в этих точках. Из графика видно, что таким значением является число − значение функции в самой точке . Поэтому получаем . Аналогично получаем, что для правого предела в точке тоже выполнено . Итак, для точки , которую естественно было бы назвать точкой непрерывности функции, выполнено: . Из утверждения (выше) об односторонних пределах их равенство означает наличие обычного предела функции в точке , равного их общему значению − значению функции в самой точке : . В точке же , как видно из приведенного графика, односторонние пределы не совпадают ( , , причем ), поэтому равенство (или, что то же самое, равенства ) не выполняется. Вот чем отличается поведение самой функции в точке (точке «непрерывности») от поведения в точке (точке «разрыва» функции). Поэтому примем следующее определение.

П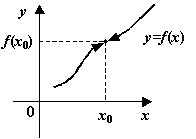 усть функция задана в некоторой окрестности точки . Эта точка называется точкой непрерывности данной функции, если выполнено: или (что то же самое) . Иллюстрация на рисунке. Далее, функция называется непрерывной на некотором интервале (a,b), если она непрерывна в каждой точке этого интервала.

Введем еще полезное для дальнейшего понятие односторонней непрерывности функции в точке. Как указано выше, функция непрерывна в точке , если , то есть выполнено 2 условия: 1) 2) . А что если одно из этих условий выполнено, а другое нет? Конечно, функцию в этом случае нельзя считать непрерывной в точке . Тогда естественно ее признать непрерывной с одной стороны (с какой − в зависимости от того, какое из равенств выполнено). Итак, пусть функция определена на полуинтервале (теперь уже можно не требовать, чтобы функция была бы определена с обеих сторон от , так как речь пойдет только о правом пределе в этой точке). Она называется непрерывной справа в точке , если выполнено . Аналогично, если функция определена на полуинтервале и выполнено , то она называется непрерывной слева в точке . Очевидно, что справедливо следующее

Утверждение. Пусть функция задана в некоторой окрестности точки . Она непрерывна в этой точке только в том случае, если она непрерывна в ней справа и слева.