Замечательные пределы
В истории математики некоторые пределы играли достаточно важную роль, однако, их вычисление не могло быть проведено привычными приемами (например, перечисленными выше), а потому для их вычисления использовались достаточно громоздкие построения и рассуждения. Эти пределы впоследствии были названы замечательными. Мы не будем проводить соответствующие доказательства, поскольку в дальнейшем появится упомянутый выше универсальный способ вычисления пределов (с помощью производных), которым вычисляются замечательные и многие другие пределы.
1.
− первый
замечательный предел.
2.
− второй
замечательный предел.
Этот предел является определением
«замечательного» числа е. Это число
играет в математике не меньшую роль,
чем известное число
.
Число е
(точнее, второй замечательный предел,
который это число определяет), возникает
естественным образом и в ряде практических
задач. Например, в задаче о банковский
процентах. Прежде, чем ее изложить,
напомним понятие процента. Один процент
от некоторого числа а
есть сотая
часть этого числа: {1
% от числа
а}
=
.
Тогда р %
от числа а,
естественно, в р
раз больше: {р%
от числа а}
=
.
Посмотрим, к какому числу
мы придем, если увеличим число
на р% :
.
Поэтому получаем правило :
(*) увеличение
числа на р% означает умножение его на
выражение
.
А теперь обещанная
Задача о банковских
процентах.
Банк дает 100 % годовых (для простоты), а
на другой срок − пропорционально
длительности срока (
года – 50 %; 1 месяц –
%;
1 день –
%
и так далее). Задача заключается в том,
чтобы выработать такую стратегию
взаимоотношений с банком в течение года
, чтобы, имея начальную сумму в а
рублей,
получить в конце года максимальную
прибыль. Сравним различные стратегии
вкладов с начальной суммой
рублей и
будем следить за суммой вклада в конце
года.
1. Первая стратегий
− самая ленивая: кладем деньги в банк
и ждем год. Тогда в конце года сумма,
очевидно, удвоится: 
;
.
2. Вторая стратегия:
кладем в банк наши а
рублей на полгода, после чего изымаем
ее вместе с набежавшими процентами, а
затем тут же все эти деньги кладем
обратно в банк на оставшиеся полгода.
Через первые полгода снятая сумма,
согласно правилу (*) (где р=50%)
, будет равна
.
В конце года полученная сумма опять
увеличится на 50%,
а потому, согласно правилу (*), мы получим
:
;
.
3. Берем с процентами
и снова кладем каждый
месяц. В конце первого месяца получим
сумму (которую сразу же положим на
следующий месяц), равную
.
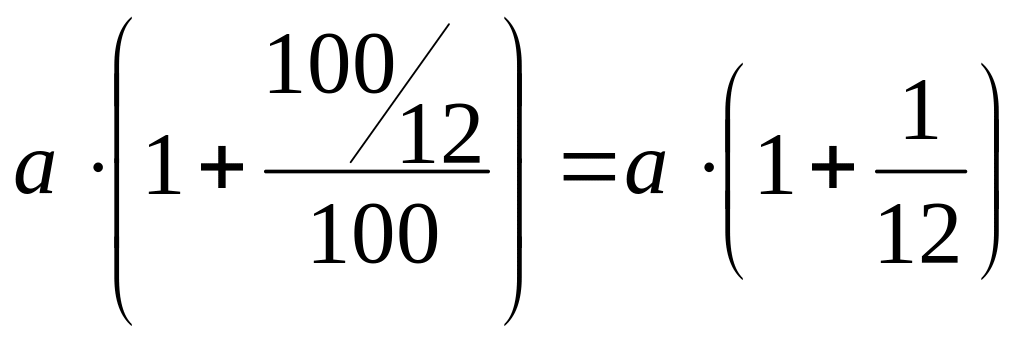Тогда в конце года получим
;
.
4. Берем-кладем
каждый день. В конце года получим сумму,
равную
;
.
Таким образом, чем
чаще мы бегаем в банк и «капитализируем»
накопившуюся сумму, тем больший доход
в конце года мы получаем. Коэффициент
увеличения вклада к концу года принимал
следующие все возрастающие значения:
2,
,
,
.
А если бегать в банк каждый час? Каждую
минуту? Возникает вопрос, возможно ли
безграничное увеличение коэффициента
умножения вклада при все учащающихся
актах капитализации вклада? Сначала мы
условно делили год на 2 части и,
соответственно, капитализировали вклад
каждые полгода (коэффициент умножения
получался
) ; потом мы делили год на 12 частей и,
соответственно, капитализировали вклад
каждый месяц (коэффициент умножения
получался
) ; затем мы делили год на 365 частей и,
соответственно, капитализировали вклад
каждый день (коэффициент умножения
получался
).
Теперь видна общая формула: если бы мы
поделили год на
частей и соответствующим образом
установили частоту капитализации
вкладов, то коэффициент умножения вклада
к концу года оказался бы равным
.
Будет ли этот коэффициент безгранично
расти при безграничном увеличении
?
Другими словами, верно ли, что
?
Однако слева получился второй замечательный
предел, а потому
. Поэтому надеяться на безграничное
увеличение вклада не приходится. Теперь
понятно, что в идеале (при переходе
процесса капитализации в непрерывный)
максимальный коэффициент увеличения
вклада равен
. В этом (ясно, что нереализуемом) случае
в конце года мы получим
рублей. Легко посчитать (попробуйте
сделать это сами), что в этом случае
годовое увеличение вклада составит
171.8
% (вместо обещанных банком 100
% ).
Точно так же можно
получить общую формулу : если банк дает
Р %
годовых, то при непрерывном процессе
«капитализации» вклада за t
лет сумма вклада будет равна
.
Эта формула носит название формулы
непрерывных процентов.